1、线性规划问题
线性规划(Linear programming,简称LP),是运筹学中研究较早、发展较快、应用广泛、方法较成熟的一个重要分支,是辅助人们进行科学管理的一种数学方法,是研究线性约束条件下线性目 标函数的极值问题的数学理论和方法。 线性规划是运筹学的一个重要分支,广泛应用于军事作战、经济分析、经营管理和工程技术等方 面。为合理地利用有限的人力、物力、财力等资源作出的最优决策,提供科学的依据。
线性规划模型的三要素
决策变量:问题中要确定的未知量,用于表明规划问题中的用数量表示的方案、措施等,可由决 策者决定和控制;
目标函数:决策变量的函数,优化目标通常是求该函数的最大值或最小值;
约束条件:决策变量的取值所受到的约束和限制条件,通常用含有决策变量的等式或不等式表示。
线性规划模型建立步骤
从实际问题中建立数学模型一般有以下三个步骤:
1.根据影响所要达到目的的因素找到决策变量
2.由决策变量和所在达到目的之间的函数关系确定目标函数
3.由决策变量所受的限制条件确定决策变量所要满足的约束条件
例题
假设有两种产品:产品A和产品B。每个单位的产品A利润为10美元,产品B利润为15美元。生产每个单位产品A需要1小时的机器时间和2小时的人工时间,生产每个单位产品B需要2小时的机器时间和1小时的人工时间。假设机器时间每天最多可用10小时,人工时间每天最多可用12小时。如何安排生产以最大化利润?
目标函数(利润最大化):
𝑍=10𝑥1+15𝑥2
约束条件:
机器时间约束:
𝑥1+2𝑥2≤10
人工时间约束:
2𝑥1+𝑥2≤12
非负约束:
𝑥1≥0
𝑥2≥0
from scipy.optimize import linprog # 目标函数系数(因为我们使用的是最小化问题,所以这里用负数表示最大化) c = [-10, -15] # 不等式左侧的系数矩阵(对应约束条件中的左侧) A = [[1, 2], [2, 1]] # 不等式右侧的值(对应约束条件中的右侧) b = [10, 12] # 非负约束的左侧系数(因为linprog默认就是非负约束,所以这里可以省略) # x_bounds = (0, None) # 如果需要显式定义,可以取消注释 # 使用linprog函数求解线性规划问题 result = linprog(c, A_ub=A, b_ub=b, method='highs') # 输出结果 if result.success: print(f'最优解:x1 = {result.x[0]}, x2 = {result.x[1]}') print(f'最大利润:{-result.fun}') else: print('没有找到最优解') # 检查约束是否满足 print('约束满足情况:') for con in result.slack: print(f'约束剩余:{con}')from scipy.optimize import linprog: 导入scipy.optimize模块中的linprog函数,用于解决线性规划问题。
c = [-10, -15]: 定义目标函数的系数。因为linprog默认是最小化问题,所以我们用负数表示最大化。
A = [[1, 2], [2, 1]]: 定义不等式约束的左侧系数矩阵。
b = [10, 12]: 定义不等式约束的右侧值。
result = linprog(...): 调用linprog函数求解问题,使用highs方法,这是一种较新的求解器,通常比默认的单纯形法更快。
if result.success: ...: 检查求解是否成功,并打印最优解和最大利润。
for con in result.slack: ...: 打印每个约束的剩余值,用于检查约束是否被满足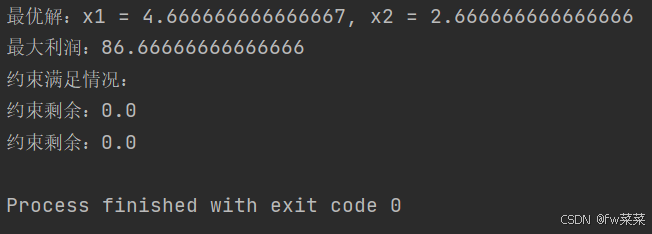
2、非线性规划
非线性规划是一种求解目标函数或约束条件中有一个或几个非线性函数的最优化问题的方法。 运筹学的一个重要分支。20世纪50年代初,库哈(H.W.Kuhn) 和托克 (A.W.Tucker) 提出了非线性规 划的基本定理,为非线性规划奠定了理论基础。这一方法在工业、交通运输、经济管理和军事等方 面有广泛的应用,特别是在“最优设计”方面,它提供了数学基础和计算方法,因此有重要的实用价值。
模型中至少一个变量是非线性,即包含 sin,log等形式 ;
线性规划有通用求准确解的方法(单纯形法),它的最优解只存在于 可行域的边界上;非线性规划的最优解(若存在)可能在其可行域的任 一点达到,目前非线性规划还没有适合各种问题的一般解法,各种方法都有其特定的适用范围;
针对数学建模来说,求近似解即可。
非线性规划中对于初始值的选取非常重要,因为非线性规划的算法求解出来的是一个局部最优 解。如果要求全局最优解,有两个思路:
给定不同的初始值,在里面找到一个最优解;
先用蒙特卡罗模拟,得到一个蒙特卡罗解,然后将这个解作为初始值来求最优解
option选项可以给定求解的算法,一共有五种,interior-point(内点法)、trust-region-ref lective(信赖域反射法)、sqp(序列二次规划法)、sqp-legacy(约束非线性优化算法)、acti ve-set(有效集法)。不同的算法有其各自的优缺点和适用情况,我们可以改变求解的算法来对比求解的结果。
fun表示目标函数,我们要编写一个独立的“m文件”储存目标函数。
下面简单介绍一下蒙特卡罗算法
定义:蒙特卡罗法又称统计模拟法,是一种随机模拟方法,以概率和统计理论方法为基础的一种计 算方法,是使用随机数(或更常见伪随机数)来解决很多计算问题的方法。将所求解的问题同一定的概 率模型相联系,用电子计算机实现统计模拟或抽样,以获得问题的近似解。为象征性地表明这一方法的 概率统计特征,故借用都城蒙特卡罗命名。
原理:由大数定理可知,当样本容量足够大时,事件的发生频率即为其概率。 • 注意:蒙特卡洛不是一种算法,准确的来说只是一种思想,或者是一种方法,只要求解的问题与概率 模型有关联,我们就可以采用这种方法,从数学建模的角度来看,蒙特卡洛是没有通用的代码的,每个问题对应的代码都是不同的。
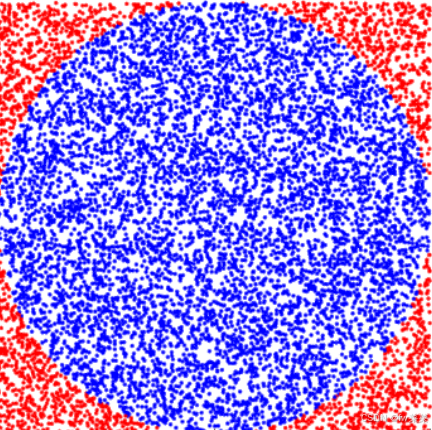
由图像求得 Π= 4 × 圆内点数/总点数
例题(用蒙特卡罗方法确定初始值,求解非线性规划问题)
以下是一个非线性规划问题的实例,我们将使用蒙特卡罗算法来选取初始值,然后使用内点法(在这个例子中,我们将使用Python的scipy.optimize库中的minimize函数,它支持多种算法,包括内点法)来解决这个问题。
非线性规划问题实例:
求解以下非线性规划问题:
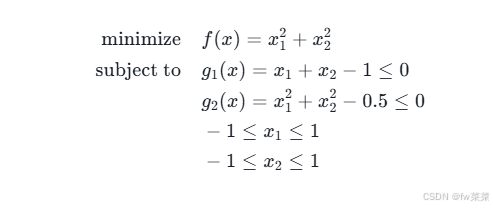
import numpy as np from scipy.optimize import minimize, Bounds # 定义目标函数 def objective(x): return x[0]**2 + x[1]**2 # 定义约束条件 def constraint1(x): return x[0] + x[1] - 1 def constraint2(x): return x[0]**2 + x[1]**2 - 0.5 # 定义边界 bounds = Bounds([-1, -1], [1, 1]) # 使用蒙特卡罗算法选取初始值 np.random.seed(0) # 设置随机种子以便结果可复现 initial_x = np.random.uniform(-1, 1, size=(2,)) # 定义约束字典 cons = ({'type': 'ineq', 'fun': constraint1}, {'type': 'ineq', 'fun': constraint2}) # 使用内点法解决问题 result = minimize(objective, initial_x, method='SLSQP', bounds=bounds, constraints=cons) # 输出结果 print("最优解:", result.x) print("最优值:", result.fun) 
3、整数规划与0/1规划
在规划问题中,有些最优解可能是分数或小数,但对于某些具体问题,常要求某些变量(全部或部分) 的解必须是整数。例如,当变量代表的是机器的台数,工作的人数或装货的车数等。为了满足整数的要 求,初看起来似乎只要把已得的非整数解舍入化整就可以了。实际上化整后的数不见得是可行解和最优 解,所以应该有特殊的方法来求解整数规划。在整数规划中,如果所有变量都限制为整数,则称为纯整 数规划;如果仅一部分变量限制为整数,则称为混合整数规划。整数规划的一种特殊情形是0-1规划(特殊的整数规划), 它的变数仅限于0或1。
例题
整数规划
假设我们是一家工厂,需要决定生产两种产品A和B的数量以最大化利润。我们有以下信息:
- 产品A的利润是每单位10美元。
- 产品B的利润是每单位6美元。
- 生产产品A需要2小时的工作时间和3平方米的原料。
- 生产产品B需要1小时的工作时间和2平方米的原料。
- 每天我们有8小时的工作时间和10平方米的原料。
- 产品A和B的生产数量必须是整数。
我们需要确定每天生产产品A和B的最佳数量以最大化总利润。
为了解决这个问题,我们将通过以下步骤来建模:
定义决策变量:
- 设 𝑥𝐴为每天生产产品A的数量。
- 设 𝑥𝐵 为每天生产产品B的数量。
建立目标函数:
- 我们的目标是最大化总利润,所以目标函数为 10𝑥𝐴+6𝑥𝐵。
建立约束条件:
- 工作时间约束:生产产品A和B所需的总工作时间不超过8小时,即 2𝑥𝐴+𝑥𝐵≤8。
- 原料约束:生产产品A和B所需的总原料不超过10平方米,即 3𝑥𝐴+2𝑥𝐵≤10。
- 产品A和B的生产数量必须是整数,即 𝑥𝐴,𝑥𝐵∈𝑍。
建立整数规划模型:
- 使用整数规划模型,因为我们的决策变量 𝑥𝐴和 𝑥𝐵 必须是整数。
import pulp # 创建一个线性规划问题 model = pulp.LpProblem("Maximize_Profit", pulp.LpMaximize) # 定义变量 x = pulp.LpVariable('x', lowBound=0, cat='Integer') # 产品A的数量 y = pulp.LpVariable('y', lowBound=0, cat='Integer') # 产品B的数量 # 定义目标函数 model += 10 * x + 6 * y, "Total Profit" # 定义约束条件 model += 2 * x + y <= 8, "Work Time Constraint" # 工作时间约束 model += 3 * x + 2 * y <= 10, "Material Constraint" # 原料约束 # 解决问题 model.solve() # 输出结果 print("Status:", pulp.LpStatus[model.status]) print("Optimal Product A Quantity:", x.varValue) print("Optimal Product B Quantity:", y.varValue) print("Maximum Profit:", pulp.value(model.objective)) 
在这个代码中,我们首先创建了一个最大化问题model。然后,我们定义了两个整数变量x和y,分别代表产品A和B的生产数量。我们添加了目标函数,即最大化总利润,并定义了两个约束条件,分别对应工作时间和原料的限制。
通过调用model.solve(),我们解决了这个整数规划问题。最后,我们打印出问题的状态、最优生产数量以及最大利润。在这个例子中,由于我们使用了整数规划,所以变量x和y的值将会是整数。
0/1规划
假设你是一家公司的经理,需要决定是否投资于几个潜在的项目。每个项目都有一个不同的投资成本、预期回报和风险等级。你有一个预算限制,并且不想投资于超过一定风险等级的项目。你的目标是在不超过预算和风险等级的情况下最大化总回报。
以下是项目的信息:
- 项目1:成本500万,回报800万,风险等级1
- 项目2:成本300万,回报600万,风险等级2
- 项目3:成本400万,回报700万,风险等级3
- 项目4:成本200万,回报500万,风险等级2
你有一个预算1000万,并且不想投资于风险等级超过2的项目。
为了解决这个问题,我们将通过以下步骤来建模:
定义决策变量:
- 设 𝑥1 为投资项目1的决策变量。
- 设 𝑥2为投资项目2的决策变量。
- 设 𝑥3 为投资项目3的决策变量。
- 设 𝑥4 为投资项目4的决策变量。
建立目标函数:
- 我们的目标是最大化总回报,所以目标函数为 800𝑥1+600𝑥2+700𝑥3+500𝑥4。
建立约束条件:
- 预算约束:所有项目的投资成本之和不超过1000万,即 500𝑥1+300𝑥2+400𝑥3+200𝑥4≤1000。
- 风险等级约束:不能投资于风险等级超过2的项目,即 𝑥3=0(因为项目3的风险等级是3)。
- 决策变量必须是非负的,即 𝑥1,𝑥2,𝑥3,𝑥4≥0。
建立整数规划模型:
- 使用整数规划模型,因为我们的决策变量 𝑥1到 𝑥4必须是整数。
import pulp # 创建一个线性规划问题,最大化总回报 model = pulp.LpProblem("Maximize_Return", pulp.LpMaximize) # 定义决策变量 x_1 = pulp.LpVariable('x_1', lowBound=0, cat='Integer') # 项目1 x_2 = pulp.LpVariable('x_2', lowBound=0, cat='Integer') # 项目2 x_3 = pulp.LpVariable('x_3', lowBound=0, cat='Integer') # 项目3 x_4 = pulp.LpVariable('x_4', lowBound=0, cat='Integer') # 项目4 # 建立目标函数 model += 800 * x_1 + 600 * x_2 + 700 * x_3 + 500 * x_4, "Total Return" # 建立约束条件 # 预算约束:所有项目的投资成本之和 <= 1000万 model += 500 * x_1 + 300 * x_2 + 400 * x_3 + 200 * x_4 <= 1000, "Budget Constraint" # 风险等级约束:项目3的风险等级超过2,因此不投资 model += x_3 == 0, "Risk Constraint for Project 3" # 解决问题 model.solve() # 输出结果 print("Status:", pulp.LpStatus[model.status]) print("Invest in Project 1:", "Yes" if x_1.varValue > 0 else "No") print("Invest in Project 2:", "Yes" if x_2.varValue > 0 else "No") print("Invest in Project 3:", "No") # 项目3的风险等级超过2,因此不投资 print("Invest in Project 4:", "Yes" if x_4.varValue > 0 else "No") print("Maximum Return:", pulp.value(model.objective)) 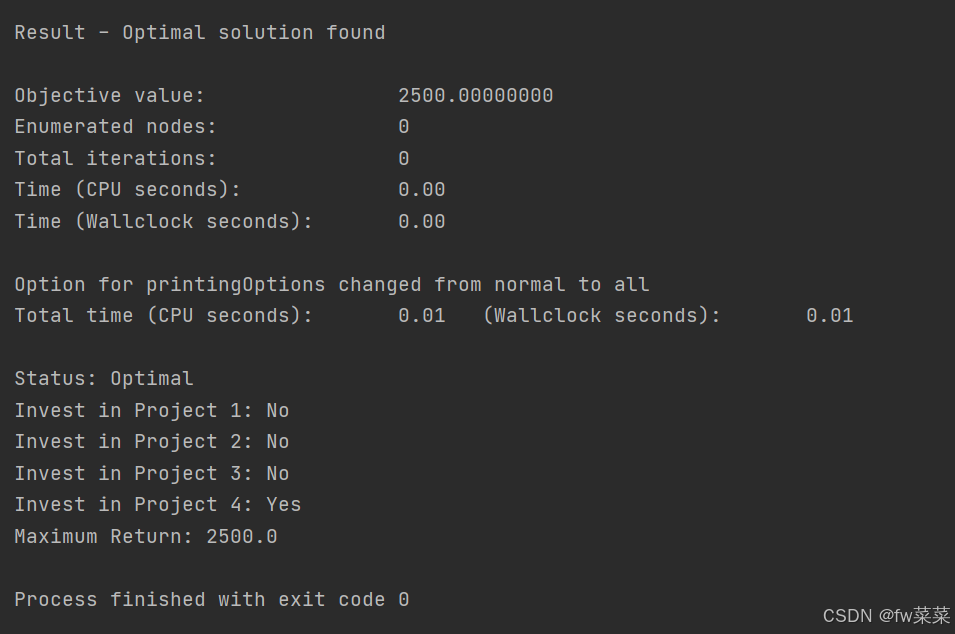
在这个代码中,我们首先创建了一个最大化问题model。接着,我们定义了四个整数变量x_1到x_4来表示是否投资于项目1到项目4。我们添加了目标函数来最大化总回报,并建立了两个约束条件来限制预算和风险等级。最后,我们调用model.solve()来解决问题,并打印出投资决策和最大回报。由于使用了整数规划,x_1到x_4的值将会是0或1,表示不投资或投资。
