阅读量:0
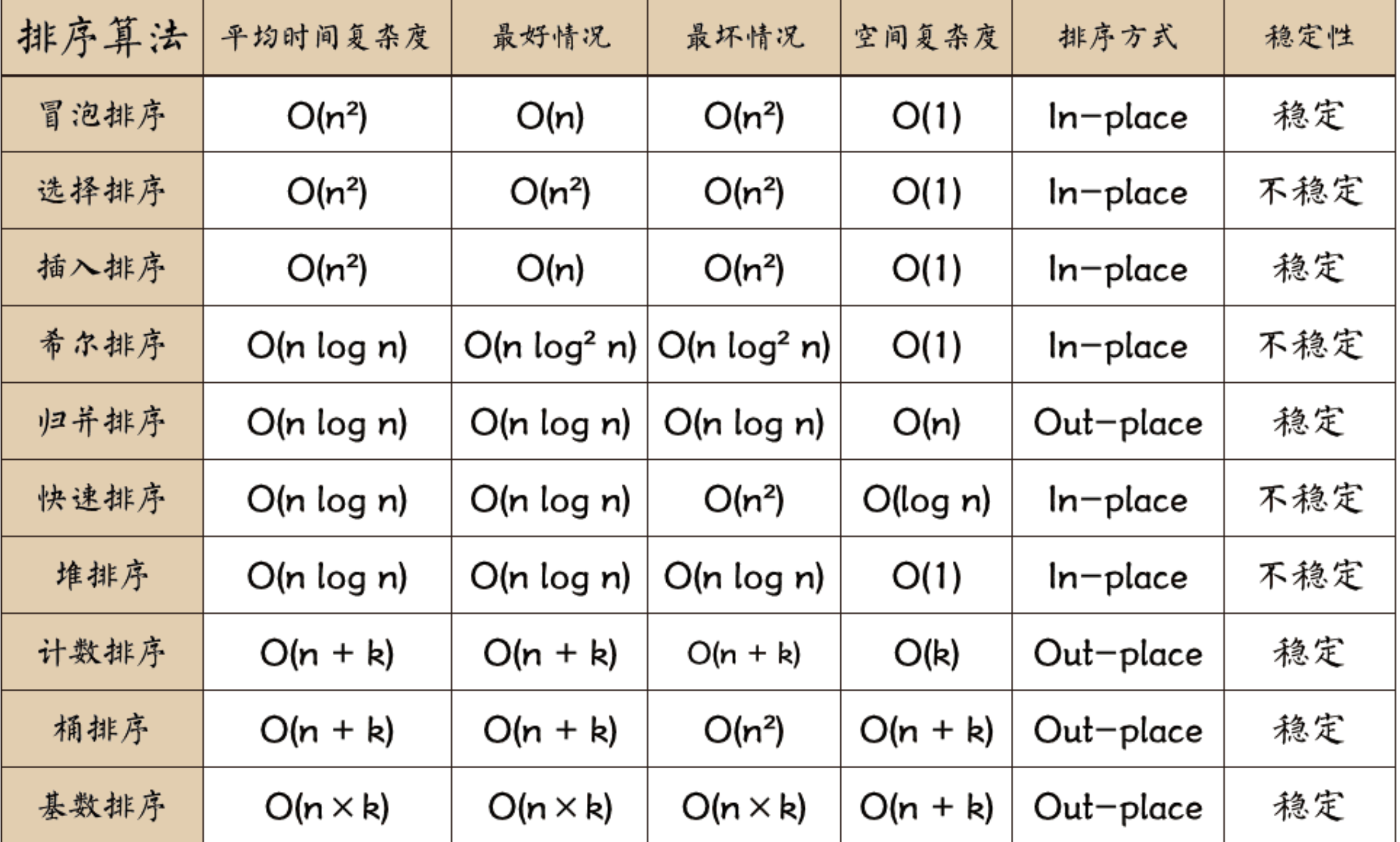
排序算法的分类
1插入:插入,折半插入,希尔
2交换:冒泡,快速
3选择:简单选择,堆
4归并:归并(不只二路归并)
5基数:
1.插入排序
void insert_sort() { for (int i = 1; i < n; i ++ ) { int x = a[i]; int j = i-1; while (j >= 0 && x < a[j]) { a[j+1] = a[j]; j -- ; } a[j+1] = x; } }2.选择排序
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理是:第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。以此类推,直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法。
void select_sort() { for (int i = 0; i < n; i ++ ) { int k = i; for (int j = i+1; j < n; j ++ ) { if (a[j] < a[k]) k = j; } swap(a[i], a[k]); } }3.冒泡排序
void bubble_sort() { for (int i = n-1; i >= 1; i -- ) { bool flag = true; for (int j = 1; j <= i; j ++ ) if (a[j-1] > a[j]) { swap(a[j-1], a[j]); flag = false; } if (flag) return; } }4.希尔排序
void shell_sort() { for (int gap = n >> 1; gap; gap >>= 1) { for (int i = gap; i < n; i ++ ) { int x = a[i]; int j; for (j = i; j >= gap && a[j-gap] > x; j -= gap) a[j] = a[j-gap]; a[j] = x; } } }5.快速排序(最快)
void quick_sort(int l, int r) { if (l >= r) return ; int x = a[l+r>>1], i = l-1, j = r+1; while (i < j) { while (a[++ i] < x); while (a[-- j] > x); if (i < j) swap(a[i], a[j]); } sort(l, j), sort(j+1, r); }6.归并排序
void merge_sort(int l, int r) { if (l >= r) return; int temp[N]; int mid = l+r>>1; merge_sort(l, mid), merge_sort(mid+1, r); int k = 0, i = l, j = mid+1; while (i <= mid && j <= r) { if (a[i] < a[j]) temp[k ++ ] = a[i ++ ]; else temp[k ++ ] = a[j ++ ]; } while (i <= mid) temp[k ++ ] = a[i ++ ]; while (j <= r) temp[k ++ ] = a[j ++ ]; for (int i = l, j = 0; i <= r; i ++ , j ++ ) a[i] = temp[j]; }7.堆排序(须知此排序为使用了模拟堆,为了使最后一个非叶子节点的编号为n/2,数组编号从1开始)
https://www.cnblogs.com/wanglei5205/p/8733524.html
void down(int u) { int t = u; if (u<<1 <= n && h[u<<1] < h[t]) t = u<<1; if ((u<<1|1) <= n && h[u<<1|1] < h[t]) t = u<<1|1; if (u != t) { swap(h[u], h[t]); down(t); } } int main() { for (int i = 1; i <= n; i ++ ) cin >> h[i]; for (int i = n/2; i; i -- ) down(i); while (true) { if (!n) break; cout << h[1] << ' '; h[1] = h[n]; n -- ; down(1); } return 0; }8.基数排序
int maxbit() { int maxv = a[0]; for (int i = 1; i < n; i ++ ) if (maxv < a[i]) maxv = a[i]; int cnt = 1; while (maxv >= 10) maxv /= 10, cnt ++ ; return cnt; } void radixsort() { int t = maxbit(); int radix = 1; for (int i = 1; i <= t; i ++ ) { for (int j = 0; j < 10; j ++ ) count[j] = 0; for (int j = 0; j < n; j ++ ) { int k = (a[j] / radix) % 10; count[k] ++ ; } for (int j = 1; j < 10; j ++ ) count[j] += count[j-1]; for (int j = n-1; j >= 0; j -- ) { int k = (a[j] / radix) % 10; temp[count[k]-1] = a[j]; count[k] -- ; } for (int j = 0; j < n; j ++ ) a[j] = temp[j]; radix *= 10; } }9.计数排序
void counting_sort() { int sorted[N]; int maxv = a[0]; for (int i = 1; i < n; i ++ ) if (maxv < a[i]) maxv = a[i]; int count[maxv+1]; for (int i = 0; i < n; i ++ ) count[a[i]] ++ ; for (int i = 1; i <= maxv; i ++ ) count[i] += count[i-1]; for (int i = n-1; i >= 0; i -- ) { sorted[count[a[i]]-1] = a[i]; count[a[i]] -- ; } for (int i = 0; i < n; i ++ ) a[i] = sorted[i]; }10.桶排序(基数排序是桶排序的特例,优势是可以处理浮点数和负数,劣势是还要配合别的排序函数)
vector<int> bucketSort(vector<int>& nums) { int n = nums.size(); int maxv = *max_element(nums.begin(), nums.end()); int minv = *min_element(nums.begin(), nums.end()); int bs = 1000; int m = (maxv-minv)/bs+1; vector<vector<int> > bucket(m); for (int i = 0; i < n; ++i) { bucket[(nums[i]-minv)/bs].push_back(nums[i]); } int idx = 0; for (int i = 0; i < m; ++i) { int sz = bucket[i].size(); bucket[i] = quickSort(bucket[i]); for (int j = 0; j < sz; ++j) { nums[idx++] = bucket[i][j]; } } return nums; }
