摘要: 本文将带你探索Python中的两个重要统计函数——var()与std()的用法及其背后的统计学意义。首先,我们会详细阐述方差的概念,它是衡量一组数值数据离散程度的关键指标,并通过实例演示如何使用numpy.var()计算样本方差与总体方差,以及ddof参数的作用。随后,我们将进一步探讨标准差,它是方差的平方根,直观反映了数据点与均值的平均偏离程度,通过numpy.std()函数实现标准差的计算。此外,文章将进一步拓展不在numpy环境下var()与std()的用法。
一、在numpy环境下的var()和std():
1.var() 函数:
var() 函数通常指的是 numpy 库中的 numpy.var() 函数,它用来计算给定数组(或一维数组的某轴向)的样本方差或者总体方差,取决于提供的参数。
样本方差:计算的是样本数据集相对于样本平均值的离散程度,计算公式为:

默认情况下:
numpy.var(a, axis=None, dtype=None, out=None, ddof=0, keepdims=False)
要在 numpy 中计算样本方差,设置 ddof=1 表示 Bessel's correction,即除以 (n - 1)。
总体方差:当 ddof=0 时,计算的是总体方差,此时除数是 n 而不是 n - 1。
import numpy as np data = np.array([1, 2, 3, 4, 5]) sample_variance = np.var(data, ddof=1) population_variance = np.var(data, ddof=0) print("样本方差:", sample_variance) print("总体方差:", population_variance)2.std() 函数:
std() 函数同样来自 numpy 库,即 numpy.std(),它是方差的算术平方根,因此提供了样本标准差或总体标准差的计算。
- 样本标准差是样本方差的非负平方根,反映的是样本数据点相对于样本均值的平均偏离程度。
- 总体标准差则对应于总体方差的平方根。
sample_std_dev = np.std(data, ddof=1) population_std_dev = np.std(data, ddof=0) print("样本标准差:", sample_std_dev) print("总体标准差:", population_std_dev)二、在pandas环境下的var()和std():
在Pandas库中,var()和std()函数可以直接应用于DataFrame或Series对象上,以计算它们的列(或行)的方差和标准差。
import pandas as pd # 创建一个简单的DataFrame data = { 'Column1': [1, 2, 3, 4, 5], 'Column2': [6, 7, 8, 9, 10] } df = pd.DataFrame(data) # 计算整个DataFrame所有列的方差 variances = df.var() # 计算单个列的方差 column1_var = df['Column1'].var() # 计算整个DataFrame所有列的标准差 std_devs = df.std() # 计算单个列的标准差 column1_std = df['Column1'].std() # 使用滚动窗口计算移动方差和标准差 df_rolling = df.rolling(window=3).agg({'Column1': ['var', 'std']}) # 输出结果 print("所有列的方差:", variances) print("Column1的方差:", column1_var) print("所有列的标准差:", std_devs) print("Column1的标准差:", column1_std) # 滚动窗口计算结果查看 print("滚动窗口内Column1的方差与标准差:") print(df_rolling.head(4)) 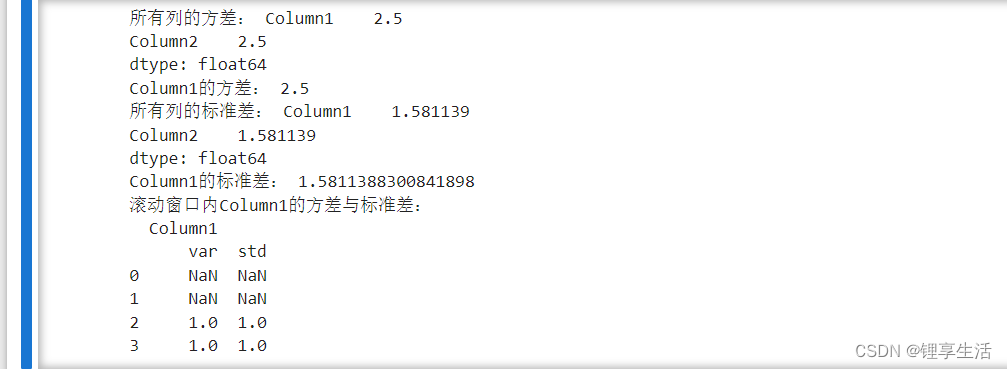
在这个例子中,df.var()和df.std()会默认计算每个变量(列)的样本方差和样本标准差。如果你想计算总体方差,对于Pandas来说没有直接的参数调整,因为Pandas遵循了NumPy的行为,默认采用ddof=1(Bessel's correction),要计算总体方差需先将数据集加1再进行计算。而滚动窗口计算则是根据指定的窗口大小滑动计算每个窗口内的方差和标准差。
补充:滚动窗是指选取了一个数字个数为3的窗口(计算3个数的方差和标准差),如1,2,3;2,3,4。因为第一行和第二行数据不足3个,故无法计算出方差和标准差。
三、在python标准库下的var()和std():
在标准Python库中并没有名为var()和std()的内置函数用于直接计算数组或列表的方差和标准差,但可以手动编写函数来实现这个功能。
def calculate_variance(lst, sample=True): n = len(lst) mean = sum(lst) / n if sample: variance = sum((xi - mean) ** 2 for xi in lst) / (n - 1) else: variance = sum((xi - mean) ** 2 for xi in lst) / n return variance def calculate_std_deviation(lst, sample=True): variance = calculate_variance(lst, sample) std_dev = variance ** 0.5 return std_dev # 示例数据 data = [1, 2, 3, 4, 5] # 计算样本方差和样本标准差 sample_variance = calculate_variance(data, sample=True) sample_std_dev = calculate_std_deviation(data, sample=True) # 计算总体方差和总体标准差 population_variance = calculate_variance(data, sample=False) population_std_dev = calculate_std_deviation(data, sample=False) print("样本方差: ", sample_variance) print("样本标准差: ", sample_std_dev) print("总体方差: ", population_variance) print("总体标准差: ", population_std_dev)