阅读量:0
决策树
决策树
1. 简介
""" 简介 一种树形结构 树中每个内部节点表示一个特征的判断 每个分支代表一个判断结果的输出 每个叶节点代表一种分类结果 建立过程 1. 特征选择 选取有较强分类能力的特征 2. 决策树生成 根据选择的特征生成决策树 3. 决策树 易过拟合 采用剪枝的方法缓解过拟合 """ 2. ID3 决策树
""" ID3 决策树 熵 Entropy 信息论中代表随机变量不确定度的度量 熵越大 数据的不确定性越高 信息越多 熵越小 数据的不确定性越低 信息熵 公式 其中 P(xi) 表示数据中类别出现的概率,H(x) 表示信息的信息熵值 信息增益 概念 特征a对训练数据集D的信息增益 定义为集合D的熵H(D)与特征a给定条件下D的熵(H|a)之差 公式 条件熵 构建流程 1. 计算每个特征的信息增益 2. 使用信息增益最大特征将数据集 拆分为子集 3. 使用该特征作为决策树的一个节点 4. 使用剩余特征对子集重复上述 1 2 3 过程 不足 偏向于选择种类多的特征作为分裂依据 """ 信息熵 公式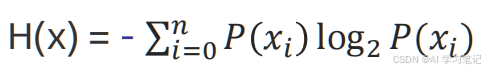
信息增益 公式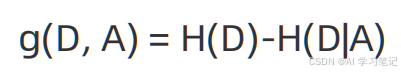
3. C4.5决策树
""" 信息增益率 信息增益率 = 信息增益 /特征熵 特征熵 本质 特征的信息增益 除以 特征的内在信息 相当于对信息增益进行修正, 增加一个惩罚系数 特征取值个数较多时 惩罚系数较小, 特征取值个数较少时, 惩罚系数较大 惩罚系数: 数据集D以特征a作为随机变量的熵的倒数 """ 信息增益率 公式
特征熵 公式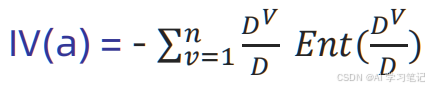
4. CART决策树
""" CART决策树 一种决策树模型, 可以用于分类 可以用于回归 回归树: 使用平方误差最小化策略 预测输出的是一个连续值 采用叶子节点里均值作为预测输出 分类生成树: 采用基尼指数最小化策略 预测输出的是一个离散值 采用叶子节点多数类别作为预测类别 基尼值 从数据集D中随机抽取两个样本,其类别标记不一致的概率 Gini(D)值越小,数据集D的纯度越高 基尼指数 选择使划分后基尼系数最小的属性作为最优化分属性 特殊说明 信息增益(ID3)、信息增益率值越大(C4.5),则说明优先选择该特征 基尼指数值越小(CART),则说明优先选择该特征 """ # 1.导入依赖包 import pandas as pd from sklearn.model_selection import train_test_split from sklearn.tree import DecisionTreeClassifier from sklearn.metrics import classification_report import matplotlib.pyplot as plt from sklearn.tree import plot_tree def titanicCase(): # 2.读数据到内存并预处理 # 2.1 读取数据 taitan_df = pd.read_csv("./data/titanic/train.csv") print(taitan_df.head()) # 查看前5条数据 print(taitan_df.info) # 查看特性信息 # 2.2 数据处理,确定x y x = taitan_df[['Pclass', 'Age', 'Sex']] y = taitan_df['Survived'] # 2.3 缺失值处理 x['Age'].fillna(x['Age'].mean(), inplace = True) print('x -->1', x.head(10)) # 2.4 pclass类别型数据,需要转数值one-hot编码 x = pd.get_dummies(x) print('x -->2', x.head(10)) # 2.5 数据集划分 x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.20, random_state=33) # 3.训练模型,实例化决策树模型 estimator = DecisionTreeClassifier() estimator.fit(x_train, y_train) # 4.模型预测 y_pred = estimator.predict(x_test) # 5.模型评估 # 5.1 输出预测准确率 myret = estimator.score(x_test, y_test) print('myret-->\n', myret) # 5.2 更加详细的分类性能 myreport = classification_report(y_pred, y_test, target_names=['died', 'survived']) print('myreport-->\n', myreport) # 5.3 决策树可视化 plot_tree(estimator, max_depth=10, filled=True, feature_names=['Pclass', 'Age', 'Sex_female', 'Sex_male'], class_names=['died', 'survived']) plt.show() 基尼值 公式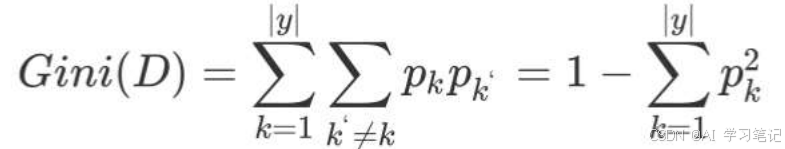
基尼指数公式
5. 决策树对比
""" 对比 ID3 信息增益 1. ID3 只能对离散属性的数据集构成决策树 2. 倾向于选择取值较多的属性 C4.5 信息增益率 1. 缓解了ID3 分支过程中总喜欢偏向于选择值较多的属性 2. 可处理连续数值型属性, 增加了对缺失值的处理方法 3. 只适合于能够驻留于内存的数据集, 大数据集无能为力 CART 基尼指数 1. 可以进行分类和回归 可处理离散属性, 也可以处理连续属性 2. 采用基尼指数 计算 量减小 3. 一定是二叉树 构建过程 1. 选择一个特征,将该特征的值进行排序, 取相邻点计算均值作为待划分点 2. 根据所有划分点, 将数据集分成两部分, R1 R2 3. R1 和 R2 两部分的平方损失相加作为该切分点平方损失 4. 取最小的平方损失的划分点, 作为当前特征的划分点 5. 以此计算其他特征的最优划分点 以及该划分点对应的损失值 6. 在所有的特征的划分点中, 选择出最小平方损失的划分点 作为当前树的分裂点 """ # 1.导入依赖包 import numpy as np import pandas as pd from sklearn.tree import DecisionTreeRegressor # 回归决策树 from sklearn.linear_model import LinearRegression import matplotlib.pyplot as plt def contrastRegressor(): """ 线性回归与回归决策树对比 :return: """ # 2.准备数据 x = np.array(list(range(1, 11))).reshape(-1, 1) y = np.array([5.56, 5.70, 5.91, 6.40, 6.80, 7.05, 8.90, 8.70, 9.00, 9.05]) print('x -->', x) print('y -->', y) # 3.模型训练,实例化模型 model1 = DecisionTreeRegressor(max_depth=1) model2 = DecisionTreeRegressor(max_depth=3) model3 = LinearRegression() model1.fit(x, y) model2.fit(x, y) model3.fit(x, y) # 4.模型预测 # 等差数组-按照间隔 x_test = np.arange(0.0, 10.0, 0.01).reshape(-1, 1) y_pre1 = model1.predict(x_test) y_pre2 = model2.predict(x_test) y_pre3 = model3.predict(x_test) print(y_pre1.shape, y_pre2.shape, y_pre3.shape) # 5.结果可视化 plt.figure(figsize=(10, 6), dpi=100) plt.scatter(x, y, label='data') plt.plot(x_test, y_pre1, label='max_depth=1') # 深度1层 plt.plot(x_test, y_pre2, label='max_depth=3') # 深度3层 plt.plot(x_test, y_pre3, label='linear') plt.xlabel('data') plt.ylabel('target') plt.title('DecisionTreeRegressor') plt.legend() plt.show() 6. 正则化 剪枝
""" 正则化-剪枝 预剪枝 指在决策树生成过程中, 对每个节点在划分前先进行估计, 若当前节点的划分不能带来决策树泛化性能提升, 则停止划分并将当前节点标记为叶节点 优点 预剪枝使决策树很多分支没有展开, 降低了过拟合风险, 显著的减少了决策树的训练和测试时间的开销 缺点 有些分支的当前划分虽不能提升泛化性能, 单后续划分却有可能导致性能的显著提高, 预剪枝决策时有欠拟合的风险 后剪枝 是先从训练集生成一颗完整的决策树, 然后自底向上地对非叶节点进行考察, 若将该节点对应的子树替换为叶节点能带来决策树泛化性能提升, 则将该子树替换为叶节点 优点 比预剪枝保留了更多的分支, 一般情况下, 后剪枝决策树的欠拟合风险很小, 泛化性能往往优于预剪枝 缺点 训练时间开销比未剪枝的决策树和预剪枝的决策树都长的多 """ 