一、前言
上次向大家介绍了一元线性回归,这次来介绍一下多远线性回归。在一元线性回归中,我们是一个x对应一个y,那么我们类比一下,所谓的多元其实就是多个x对应一个y。我们要根据多个自变量的值来预测我们想要的因变量。
二、多元线性回归
表达式:h(x)=a0+a1x1+a2x2+......
所以要确定这个回归函数的关键在于要确定a0、a1、a2....等回归系数(也可以叫做权重)
如何确定呢?
①:最小二乘法
根据一元线性回归的方程的求解方法,我们依然可以用我们的最小二乘法来求解我们多元线性函数中的回归系数,等式如下:
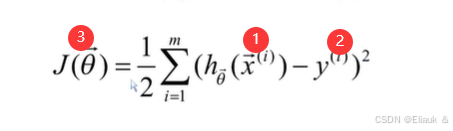
在这个表达式中,①代表我们的估计值,②代表我们的真实值,m代表具体的实例数,1/2是方便我们求导计算,③则代表我们要求的回归系数。因为①和②的数据都是知道的,我们只需对所求的a0、a1、a2...等系数求偏导让其等于0,将①和②数据代入,求出对应值即可。
②:梯度下降法
之所以这里提到使用梯度下降法来求解参数,是因为并不是函数都是可以通过求导数取得0值的点来得到我们想要的数据的。很多时候,让导数等于0的那个点的函数方程解不出来,此时我们通过计算机来不断地尝试、迭代从而找到合适的值,可能是很好的选择。梯度下降法的使用贯穿我们的整个机器学习的过程,很重要,我会单独写一篇博客来详细介绍一下这个算法,这里就不赘述了。
三、实践
我们跟着这个老师的案例来写一下demo,这样可以让我们对这个算法有更深刻的理解。
案例:

代码:
import numpy as np from sklearn import linear_model A = [250, 360, 165, 43, 92, 200, 355, 290, 230, 120, 73, 205, 400, 320, 72, 272, 94, 190, 235, 139] B = [35, 29, 36, 60, 65, 30, 10, 70, 21, 55, 54, 48, 20, 39, 60, 20, 58, 40, 27, 30] C = [3, 4, 7, 6, 5, 5, 6, 10, 9, 2, 12, 5, 5, 4, 8, 5, 7, 8, 9, 7] D = [6, 10, 3, 9, 6, 5, 7, 10, 11, 5, 4, 1, 15, 7, 6, 8, 3, 11, 8, 5] x = np.array([B, C, D]).T y = np.array(A).reshape(-1, 1) lr = linear_model.LinearRegression() lr.fit(x, y) print(lr.coef_) print(lr.intercept_) test = np.array([30, 5, 10]).reshape(1, 3) print('取暖费为:', lr.predict(test))思路:先将数据分为两类分别是x与y,然后调用我们的SKlearn库下的linear_model.LinearRegression()模型函数,再通过fix()调用模型,最后因为我们需要做预测,则需要将我们的test数据传入我们的预测函数predict()中预测结果即可。
效果:

四、总结
博主也是初学者,有很多不懂的地方,如果有说错的地方,欢迎大家指正。最后,该内容是跟着B站up主【abilityjh】老师学习的,大家可以去看该老师的视频学习!
