floodfill算法一

点赞👍👍收藏🌟🌟关注💖💖
你的支持是对我最大的鼓励,我们一起努力吧!😃😃
1.floodfill算法简介
floodfill算法又叫洪水灌溉或者洪水淹没啥的,这个算法
比如有一个区域,负数表示低谷,0表示平原,正数表示山峰。此时发大水把这些区域淹了。其中平原和山峰可能不会改变,但是低谷水位就要上升。这种类型题目就是,我们要在这个区域中找出水位会上升的区域或者说找到会被洪水淹的区域。其实这道题说白了就是把 性质相同的一个连通块 找出来。
比如这里就是把所有是负数的连通块找到,注意只能上下左右相连,斜着不能连!
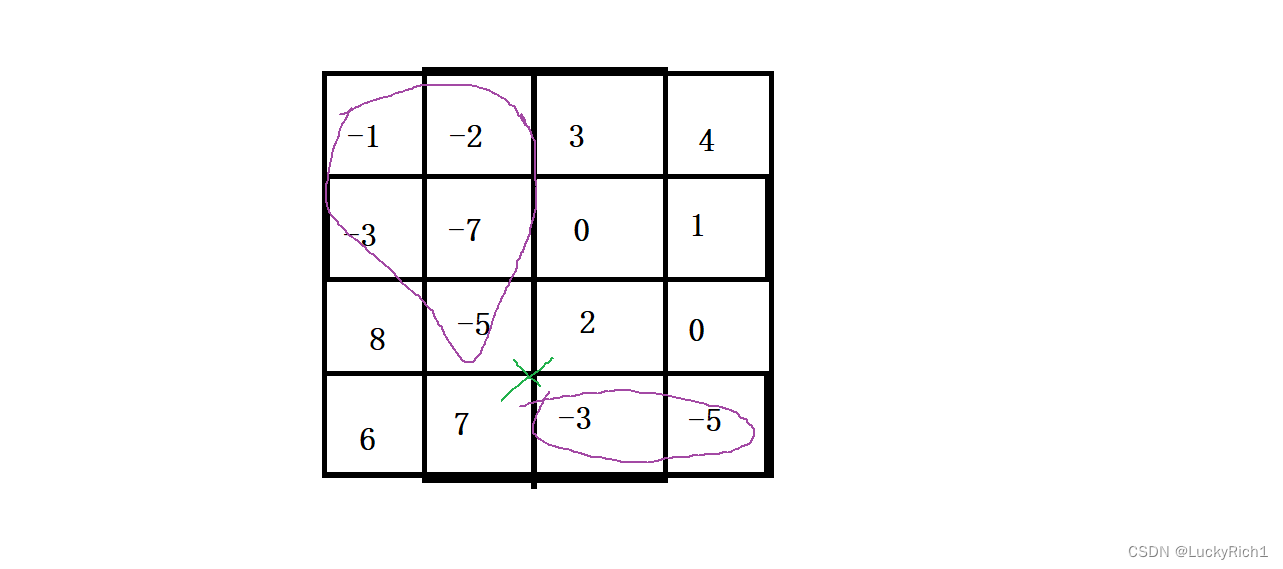
floodfill算法解决的问题就这么简单,它解决方法也非常简单,可以用深度优先遍历和宽度优先遍历。dfs就是一条路走到黑,如果无法走就回溯到上一层,然后能走就继续走,直到走到一个不能走的位置。此时就把一个连通区域找到了。
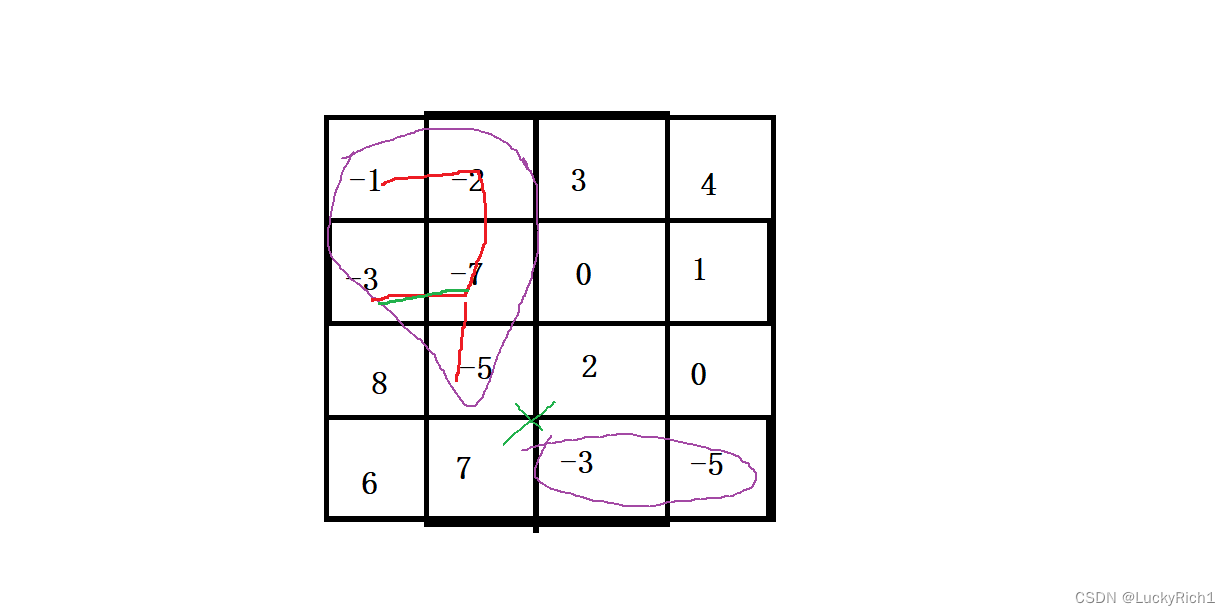
bfs从一个位置开始把和我相连的位置加入到队列里,然后继续在扩一层在扩一层…
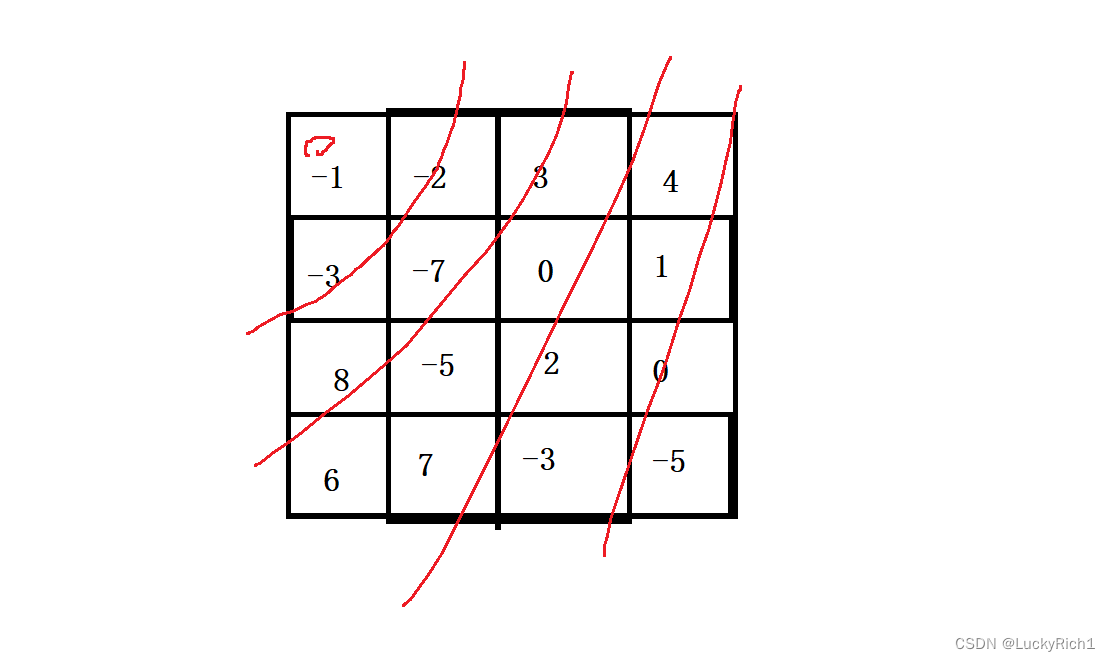
因此floodfill算法有两种解决方式,要么dfs、要么bfs。你会发现这个dfs和我们前面单词搜索,黄金矿工解法非常相似,到一个位置之后就上下左右扫描,当和我性质相同就递归进去。这里主要用的是dfs。bfs在优先算法里面,本质其实就是暴搜。
2.图像渲染
题目连接:733. 图像渲染
题目分析:

题目说这么多,其实就是给一个矩阵,在给一个初始的坐标,然后把和这小格性质相同的连通块找到然后变成newcolor。注意只能上下左右去找!
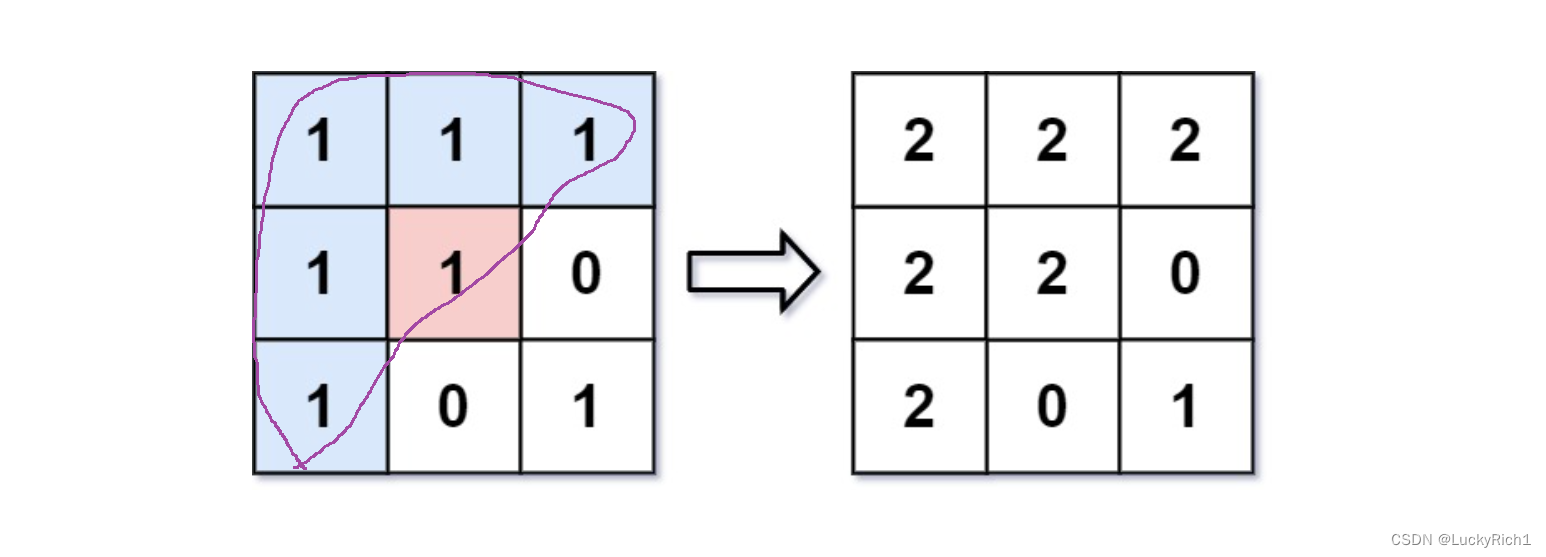
算法原理:
有我们之前做那么多题基础,这里不应该是问题。我们只是简单把过程说一下。其他都是差不多。这里我们只用进行一次深度优先遍历就可以了。以初始位置为起点开始上下左右扫描,当我扫描到和我相同的像素值的时候我就递归进去,但是在递归进去之前先要把我当前位置的值改成newcolor。如果递归到某个位置它上下左右都走不了就回溯。然后如果能走就继续递归下去。直到把这次性质相同的连通块走完。
有一个细节问题,如果newcolor就等于给我们初始位置值,如 newcolor=1,那我们刚才的策略就有问题了。因为上下左右递归的时候可能会回到上一次递归,就会造成死递归。当原始的值和要修改的值相同的话,我们要把这个情况特殊出来一下。无需修改直接返回即可!

class Solution { int dx[4]={0,0,1,-1}; int dy[4]={1,-1,0,0}; int m,n; int prev; public: vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color) { if(image[sr][sc] == color) return image; m=image.size(),n=image[0].size(); prev=image[sr][sc]; dfs(image,sr,sc,color); return image; } void dfs(vector<vector<int>>& image, int i, int j, int color) { image[i][j]=color; for(int k = 0; k < 4; ++k) { int x = i + dx[k],y = j + dy[k]; if(x >= 0 && x < m && y >= 0 && y < n && image[x][y] == prev) { dfs(image,x,y,color); } } } }; 3.岛屿数量
题目链接:200. 岛屿数量
题目分析:

这道题让找到由陆地构成的岛屿的数量,也就是让找到性质相同的连通块数量。注意只能上下左右找。1代表陆地,0代表水域。
算法原理:
我们一行一行扫描扫描到第一个1的时候,我就把以这个1相连的所有为1的区域都标记一下,相当于找到了一块岛屿记录一下。接下来继续扫描。但是有可能会碰到重复的情况,因此这里需要一个bool类型的数组 标记当前位置是否被找过。或者可以修改原始值把它由1变成0。这里我们还用的是老方法bool类型数组。之前走过下一就不能在走了。

class Solution { //bool vis[301][301]; //感觉浪费空间就先计算一下当前需要多大空间,然后再申请空间 vector<vector<int>> vis; int dx[4]={0,0,1,-1}; int dy[4]={1,-1,0,0}; int m,n; public: int numIslands(vector<vector<char>>& grid) { int cnt = 0; m = grid.size(),n = grid[0].size(); vis=vector<vector<int>>(m,vector<int>(n)); for(int i = 0; i < m; ++i) { for(int j = 0; j < n; ++j) { if(!vis[i][j] && grid[i][j] == '1' ) { vis[i][j]=true; dfs(grid,i,j); ++cnt; } } } return cnt; } void dfs(vector<vector<char>>& grid,int i,int j) { for(int k = 0; k < 4; ++k) { int x = i + dx[k], y = j + dy[k]; if(x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && grid[x][y] == '1') { vis[x][y]=true; dfs(grid, x, y); } } } }; 4.岛屿的最大面积
题目链接:695. 岛屿的最大面积
题目分析:

上面是让找岛屿数量,这里让找岛屿面积最大,思想几乎是一模一样
算法原理:
我们用的肯定还是深度优先遍历,此时依旧是一行一行扫描,当扫描到一个陆地之后就由这个陆地开始来一次深度优先遍历,但是此时做深度优先遍历我们可以搞一个变量count 全局和参数都可以,只要进入一次dfs,就让count++。当这个深度优先遍历结束之后此时这个count就是统计这个岛屿的面积。然后让一个ret统计所有count里面的最大值,就可以把最大岛屿面积找到了。
class Solution { bool vis[51][51]; int dx[4]={0,0,1,-1}; int dy[4]={1,-1,0,0}; int m,n; int count; public: int maxAreaOfIsland(vector<vector<int>>& grid) { m = grid.size(),n = grid[0].size(); int ret=0; for(int i = 0; i < m; ++i) { for(int j = 0; j < n; ++j) { if(!vis[i][j] && grid[i][j] == 1) { count=0;//每次进来先恢复一下最开始面积数 dfs(grid,i,j); ret=max(ret,count); } } } return ret; } void dfs(vector<vector<int>>& grid,int i,int j) { count++; vis[i][j]=true; for(int k = 0; k < 4; ++k) { int x = i + dx[k], y = j + dy[k]; if(x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && grid[x][y] == 1) { dfs(grid, x, y); } } } }; 