一.LCR 152. 验证二叉搜索树的后序遍历序列
题目描述:
给你一个二叉搜索树的后续遍历序列,让你判断该序列是否合法。
解题思路:
根据二叉搜索树的特性,二叉树搜索的每一个结点,大于左子树,小于右子树。所以二叉搜索树的中序遍历,本身就是一个有序的序列。由此我们看看二叉搜索树的后续遍历,后续遍历的顺序是,根,右子树,左子树。所以我们后续遍历的第一个结点就是根节点,后面遇到的若干个比根节点大的结点就是右子树结点,剩下的结点就都是左子树结点。根据这个规律就可以轻松的将二叉搜索树,划分出来。并且判断是否合法。然后将左右子树继续递归下去。
代码:
class Solution { public: //二叉搜索树后续遍历特点,左 右 根,天然将数据划分为三部分 //最右边一个是根 //中间部分比根大 //左边部分比跟小 //同时中间部分和,左边部分又都是两部分子树 bool dfs(vector<int>& postorder,int l,int r,int i) { //一个节点的树满足二叉搜索是树 if(l>=r)return true; //获取根的值 int root=postorder[i]; i--; //获取右子树,右子树结点值大于根来判断右子树 while(i>=l&&postorder[i]>=root) { i--; } //获取左子树,剩下的都是左子树值 int next=i; while(next>=l) { //左子树的值应全部小于根,由于此左子树的依赖上面的右子树, //如果左子树没有提,右子树也就没有问题 if(postorder[next]>=root)return false; next--; } return dfs(postorder,l,next,next)&&dfs(postorder,next+1,r-1,r-1); } bool verifyTreeOrder(vector<int>& postorder) { //左 右 根 //小 大 等 int r=postorder.size()-1; return dfs(postorder,0,r,r); } };二. LCR 003. 比特位计数
题目描述:
给出一个整数n,给出0~n之间每个整数的二进制中出现1的个数,结果返回一个数组。
思路描述:
没啥好的思路,打印出来找规律,规律如下。

出来0之外的后面没2的次方个数,就是前面所有加1.
代码:
class Solution { public: vector<int> countBits(int n) { vector<int>ans; ans.push_back(0);//初始化 int num = 1,m=1; while(num<=n) { for (int i = 0; i < m && num <= n; i++, num++) { ans.push_back(ans[i] + 1); } m *= 2;//每次记得把m*=2,m就是2^x, } return ans; } }; 三.LCR 004. 只出现一次的数字 II
题目描述:
给出一个数组arr,除了一个只出现一次以外,数组中的数都出现了三次。求出只出现一次的那个数 x。
解题思路:
(1)哈希表统计最简单
(2)位运算
位运算主要通过计算32位比特位中,每一位在上述数组中出现的1次数,且第i位出现出现1的次数的可能只有三个,3n,3n+1,0。3n和0代表 x 中第i为不是1,3n+代表x的第i位是1.
这样我们可以得到只出现一次的数每一位比特位了。
代码:
class Solution { public: int singleNumber(vector<int>& nums) { long ret=0; //遍历每一个元素的32个比特位 //切记不能从低位 往 高位遍历,从遇到的第一位为1才开始算数值有效位 for(int i=31;i>=0;i--) { int bits=0; for(auto e:nums) { if(e&(1<<i))bits++; } bits%=3; //在遇到1之前ret一直是0 ret=ret*2+bits; } return ret; } }; 四.LCR 011. 连续数组
题目描述:
给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组,并返回该子数组的长度。
思路描述:
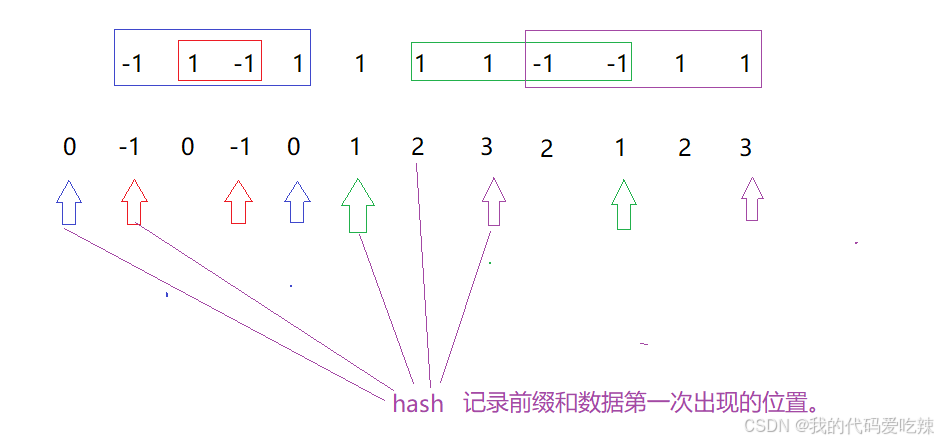
思路转换将数组中的0换成-1,那么问题就变成找到区间和为0的最长连续子数组,并返回该子数组的长度。
(1)dp:dp[i][j]代表i~j之间的和。
(2)前缀和,本质还是dp
(3)前缀和+哈希表
前缀和处理之后的数组之间是由规律的:
相同的前缀和之间的数(x,y],加一起就是0.hash表记录前缀和数据第一次出现的位置,后面再出现就可以直接求出长度。