

登神长阶
第八神装 TreeSet
第九神装 TreeMap
目录
💉 一.二叉搜索树
首先我们要知道TreeSet/TreeMap底层都采用的都是一种二叉搜索树(也叫自平衡二叉树),因此我们先来了解一下二叉搜索树。
对于他的学习若之前没有了解的可以参考:Java 【数据结构】 二叉树(Binary_Tree)【神装】
🩸1. 定义
二叉搜索树(Binary Search Tree,简称BST),是一种特殊的二叉树,它具有以下性质:
- 每个节点都有一个键(Key)和两个指向其他节点的指针(左子指针和右子指针)。
- 任意节点的左子树中的所有键都小于该节点的键。
- 任意节点的右子树中的所有键都大于该节点的键。
- 左右子树也都是二叉搜索树。
- 不存在键值相等的节点。
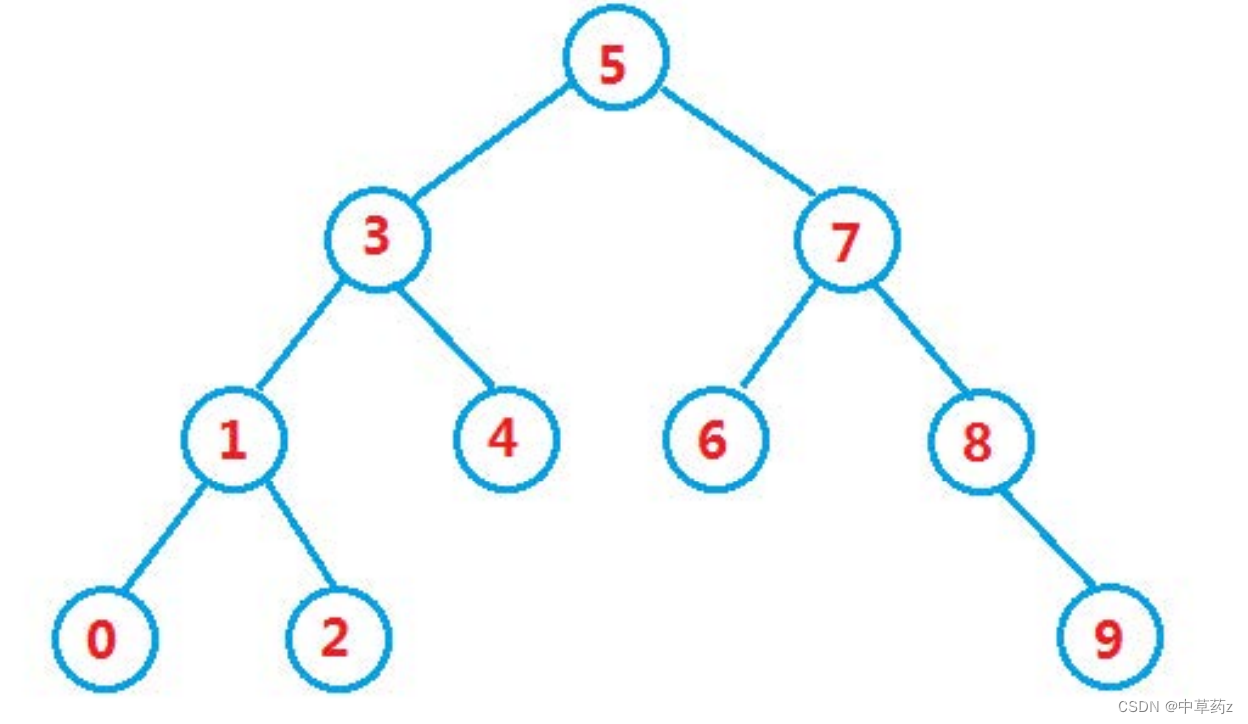
在Java中,我们可以这样定义一个二叉搜索树:
public class BinarySearchTree { private class Node { int val; Node left; Node right; Node(int val) { this.val = val; left = null; right = null; } } private Node root; // 构造函数、插入方法、查找方法、删除方法等... } 💊2. 基本操作
二叉搜索树支持以下基本操作:
- 插入(Insert):向树中插入一个新节点,保持树的二叉搜索性质。
- 查找(Search):在树中查找一个特定的节点。
- 删除(Delete):从树中删除一个节点,并保持树的二叉搜索性质。
- 遍历(Traverse):对树进行遍历,常用的遍历方式有前序、中序和后序遍历。
接下来我们详细介绍一下它的各个操作,因为后续二叉树本身是数据结构中一个很关键的知识点,像红黑树,AVL树等等,我们需要牢牢掌握!
🩹3. 插入操作
插入操作的步骤如下:
- 创建新节点。
- 比较新节点的键与根节点的键:
- 如果新节点的键小于根节点的键,则将新节点插入到根节点的左子树中。
- 如果新节点的键大于根节点的键,则将新节点插入到根节点的右子树中。
- 如果插入点是空,则直接在新位置插入新节点。
- 如果插入点非空,则递归地在相应子树中进行插入操作。
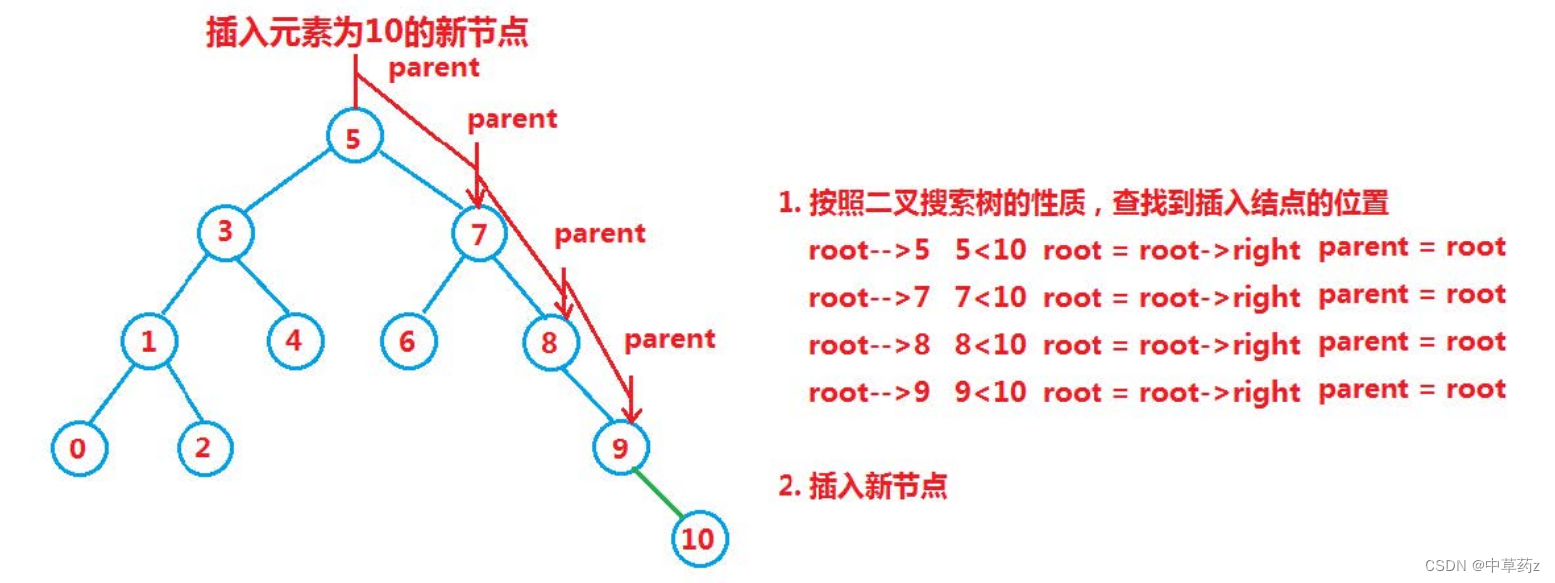
代码:
/** * 插入一个元素 * @param key */ public void insert(int key) { TreeNode node=new TreeNode(key); //若该搜索树为空,则直接作为根节点; if (root==null){ root=node; } TreeNode cur=root; TreeNode parent=null; while(cur!=null){ if (cur.key<key){ parent = cur; cur=cur.right; }else if(cur.key>key){ parent = cur; cur=cur.left; }else{ return ; } } if (parent.key>key){ parent.left=node; }else{ parent.right=node; } }🩼4. 查找操作
查找操作的步骤如下:
- 从根节点开始比较。
- 如果查找的键小于当前节点的键,则递归地在左子树中查找。
- 如果查找的键大于当前节点的键,则递归地在右子树中查找。
- 如果找到节点,则返回该节点。
- 如果没有找到,则返回null。
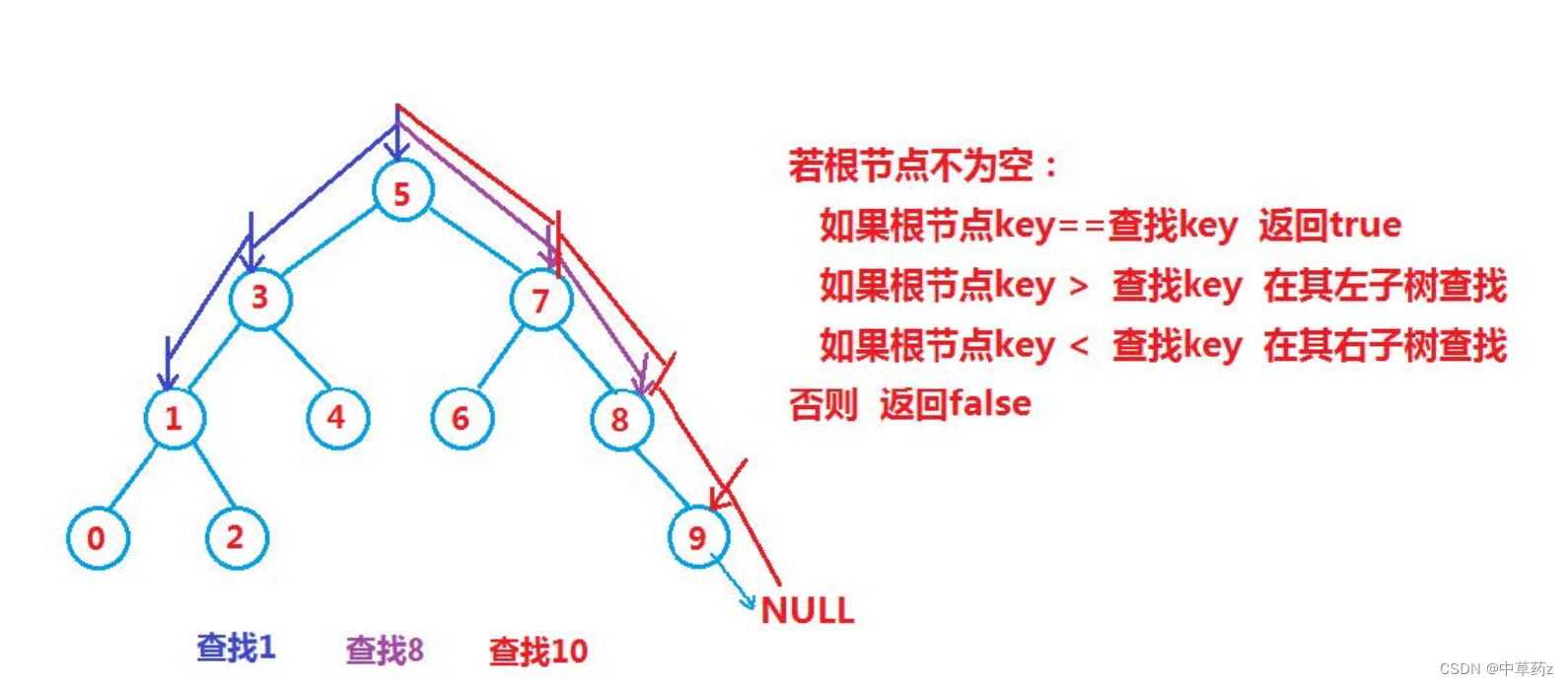
代码
//查找key是否存在 public TreeNode search(int key) { TreeNode cur =root; while(cur!=null){ if (cur.key<key){ cur=cur.right; }else if(cur.key>key){ cur=cur.left; }else{ return cur; } } return null; }🩺5. 删除操作*
设待删除结点为 cur, 待删除结点的双亲结点为 parent 1. cur.left == null- cur 是 root,则 root = cur.right
- cur 不是 root,cur 是 parent.left,则 parent.left = cur.right
- cur 不是 root,cur 是 parent.right,则 parent.right = cur.right
- cur 是 root,则 root = cur.left
- cur 不是 root,cur 是 parent.left,则 parent.left = cur.left
- cur 不是 root,cur 是 parent.right,则 parent.right = cur.left
- 需要使用替换法进行删除,即在它的右子树中寻找中序下的第一个结点(关键码最小),用它的值填补到被删除节点中,再来处理该结点的删除问题
代码
//删除key的值 public boolean remove(int key) { TreeNode cur =root; TreeNode parent=null; while(cur!=null){ if (cur.key>key){ parent=cur; cur=cur.left; }else if (cur.key<key){ parent=cur; cur=cur.right; }else{ removeNode(parent,cur); return true; } } return false; } public void removeNode(TreeNode parent,TreeNode cur){ if (cur.left==null){//左子树为空 if (cur==root){ root=cur.right; }else if(cur==parent.left){ parent.left=cur.right; }else{ parent.right=cur.right; } }else if (cur.right==null){//右子树为空 if (cur==root){ root=cur.left; }else if (cur==parent.left){ parent.left=cur.left; }else{ parent.right=cur.left; } }else{//左右子树都不为空 右子树的最小值代替 TreeNode targetp=cur; TreeNode target=cur.right; while(target!=null){ targetp=target; target=target.left; } cur.key=target.key; //删除原本数值 if (targetp.left==target){ targetp.left=target.left; }else{ targetp.right=target.right; } } }🩻6. 遍历操作
二叉搜索树的遍历操作与普通二叉树相同,可以使用前序、中序和后序遍历。
中序遍历会按照从小到大的顺序访问所有节点,是一个有序数列
前序遍历代码举例
public void prevOreder(TreeNode root){ if (root==null){ return; } prevOreder(root.left); System.out.print(root.key+" "); prevOreder(root.right); }其余遍历方式,包括非递归的遍历方式: Java 【数据结构】 二叉树(Binary_Tree)【神装】
🪒7.性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能。对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数,即结点越深,则比较次数越多。 但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:
最优情况下,二叉搜索树为完全二叉树,其平均比较次数为:log N最差情况下,二叉搜索树退化为单支树,其平均比较次数为:N/2
🪥二.TreeSet
🧽1. 定义
TreeSet是Java集合框架中的一种有序集合,它实现了Set接口,因此具有不允许重复元素的特性。与HashSet不同,TreeSet使用红黑树数据结构来存储元素,这使得元素在集合中保持有序。

🧻 2.操作
| 方法 | 解释 |
| boolean add(E e) | 添加元素,但重复元素不会被添加成功 |
| void clear() | 清空集合 |
| boolean contains(Object o) | 判断 o 是否在集合中 |
| Iterator<E> iterator() | 返回迭代器 |
| boolean remove(Object o) | 删除集合中的 o |
| int size() | 返回set中元素的个数 |
| boolean isEmpty() | 检测set是否为空,空返回true,否则返回false |
| Object[] toArray() | 将set中的元素转换为数组返回 |
| boolean containsAll(Collection<?> c) | 集合c中的元素是否在set中全部存在,是返回true,否则返回 false |
| boolean addAll(Collection<? extends E> c) | 将集合c中的元素添加到set中,可以达到去重的效果 |
import java.util.TreeSet; public class TreeSetExample { public static void main(String[] args) { // 创建一个TreeSet,元素自然排序(升序) TreeSet<Integer> numbers = new TreeSet<>(); // 添加一些元素 numbers.add(5); numbers.add(3); numbers.add(8); numbers.add(1); // 打印整个TreeSet System.out.println("TreeSet: " + numbers); // 查找是否存在某个元素 System.out.println("Contains 6: " + numbers.contains(6)); // 删除一个元素 numbers.remove(3); System.out.println("TreeSet after removing 3: " + numbers); // 遍历TreeSet System.out.println("Traversing TreeSet:"); for (int number : numbers) { System.out.println(number); } // 排序和检索操作 System.out.println("First element: " + numbers.first()); System.out.println("Last element: " + numbers.last()); System.out.println("Element greater than 4: " + numbers.higher(4)); System.out.println("Element lower than 4: " + numbers.lower(4)); } } 🪣3. Set主要特性
- Set是继承自Collection的一个接口类
- TreeSet中不能插入null的key,HashSet可以。
- 实现Set接口的常用类有TreeSet和HashSet,还有一个LinkedHashSet,LinkedHashSet是在HashSet的基础上维护了一个双向链表来记录元素的插入次序。
- 有序性:元素按照自然顺序或者根据提供的Comparator进行排序。当向
TreeSet中添加元素时,会根据元素之间的比较关系进行自动排序。 - 不可重复性:TreeSet中的元素不允许重复。Set最大的功能就是对集合中的元素进行去重
- 基于红黑树实现:通过红黑树数据结构实现了有序的、唯一元素存储。
| Set底层结构 | TreeSet |
| 底层结构 | 红黑树 |
| 插入/删除/查找时间 复杂度 | O(log N) |
| 是否有序 | 关于Key有序 |
| 线程安全 | 不安全 |
| 插入/删除/查找区别 | 按照红黑树的特性来进行插入和删除 |
| 比较与覆写 | key必须能够比较,否则会抛出 ClassCastException异常 |
| 应用场景 | 需要Key有序场景下 |
🫧4. TreeSet的内部实现
TreeSet通过红黑树(Red-Black Tree)数据结构实现了有序的、唯一元素存储。红黑树是一种自平衡的二叉查找树,在插入和删除操作后能够保持相对较低的高度,从而保证了检索、插入和删除操作的时间复杂度为O(log n)。
🛒5. 应用场景
TreeSet适用于需要保持元素有序并且去除重复元素的场景。由于其基于红黑树实现,可以高效地支持元素的查找、插入和删除操作。因此,在需要有序集合且不允许重复元素的情况下,TreeSet是一个十分实用的选择。总而言之:
- 当需要保持元素的有序性且不允许重复时,
TreeSet是一个很好的选择。 - 常用于需要按照特定顺序处理元素的情况。
🧯三.TreeMap
🧹1.定义
TreeMap是基于红黑树数据结构的键值对映射。它保证键的有序性,键按照其自然顺序(通过键的compareTo方法确定的顺序)进行排序。

🪤2.操作
| 方法 | 解释 |
| V get(Object key) | 返回 key 对应的 value |
| V getOrDefault(Object key, V defaultValue) | 返回 key 对应的 value,key 不存在,返回默认值 |
| V put(K key, V value) | 设置 key 对应的 value |
| V remove(Object key) | 删除 key 对应的映射关系 |
| Set<K> keySet() | 返回所有 key 的不重复集合 |
| Collection<V> values() | 返回所有 value 的可重复集合 |
| Set<Map.Entry<K, V>> entrySet() | 返回所有的 key-value 映射关系 |
| boolean containsKey(Object key) | 判断是否包含 key |
| boolean containsValue(Object value) | 判断是否包含 value |
import java.util.Map; import java.util.TreeMap; public class TreeMapExample { public static void main(String[] args) { // 创建一个 TreeMap TreeMap<Integer, String> treeMap = new TreeMap<>(); // 向 TreeMap 中添加键值对 treeMap.put(1, "value1"); treeMap.put(2, "value2"); treeMap.put(3, "value3"); treeMap.put(4, "value4"); treeMap.put(5, "value5"); // 打印 TreeMap System.out.println("TreeMap: " + treeMap); // 获取一个键对应的值 String value = treeMap.get(3); System.out.println("Value for key 3: " + value); // 删除一个键值对 boolean removed = treeMap.remove(2); System.out.println("Remove key 2: " + removed); // 获取 TreeMap 的大小 int size = treeMap.size(); System.out.println("Size of TreeMap: " + size); // 检查 TreeMap 是否为空 boolean isEmpty = treeMap.isEmpty(); System.out.println("Is TreeMap empty: " + isEmpty); // 遍历 TreeMap for (Map.Entry<Integer, String> entry : treeMap.entrySet()) { System.out.println("Key: " + entry.getKey() + ", Value: " + entry.getValue()); } } } 🧷3.Map的主要特性
- Map是一个接口,不能直接实例化对象,如果要实例化对象只能实例化其实现类TreeMap或者HashMap
- Map中存放键值对的Key是唯一的,value是可以重复的
- 在TreeMap中插入键值对时,key不能为空,否则就会抛NullPointerException异常,value可以为空。但是HashMap的key和value都可以为空。
- Map中的Key可以全部分离出来,存储到Set中来进行访问(因为Key不能重复)。
- Map中的value可以全部分离出来,存储在Collection的任何一个子集合中(value可能有重复)。
- Map中键值对的Key不能直接修改,value可以修改,如果要修改key,只能先将该key删除掉,然后再来进行重新插入。
| Map底层结构 | TreeMap |
| 底层结构 | 红黑树 |
| 插入/删除/查找时间 复杂度 | O(log N) |
| 是否有序 | 关于Key有序 |
| 线程安全 | 不安全 |
| 插入/删除/查找区别 | 需要进行元素比较 |
| 比较与覆写 | key必须能够比较,否则会抛出 ClassCastException异常 |
| 应用场景 | 需要Key有序场景下 |
🧿4. TreeMap的内部实现
TreeMap的内部实现是通过红黑树来存储键值对的。红黑树是一种自平衡的二叉查找树,它保证了在插入和删除操作后,树的高度保持相对较低,从而保证了高效的查找、插入和删除操作。
🪬5.应用场景
在实际应用中,如果你需要一个有序的映射表,并且不允许键重复,那么TreeMap是一个很好的选择。它既满足了有序性的需求,又提供了高效的操作性能。总而言之:
- 当需要保持键的有序性且需要根据键快速查找值时,
TreeMap是一个很好的选择。 - 常用于需要按照特定顺序处理键值对的情况。
🗿四.总结与反思
人们在一起可以做出单独一个人所不能做出的事业;智慧+双手+力量结合在一起,几乎是万能的。——韦伯斯特
在学习二叉搜索树和TreeSet/TreeMap的过程中,我深刻体会到了数据结构在编程中的应用和重要性。二叉搜索树作为一种特殊的二叉树,其特性包括每个节点的左子树都比当前节点小,右子树都比当前节点大,这使得在二叉搜索树中进行查找、插入和删除操作的时间复杂度可以达到O(log n),相比于线性搜索的O(n)有了显著的提升。而TreeSet和TreeMap的底层实现正是基于这种高效的数据结构——红黑树。
红黑树是一种自平衡的二叉查找树,它通过红黑规则来保持树的平衡,确保任何节点的左子树的高度最多比右子树高1,从而保证了树的平衡性。在TreeSet和TreeMap中,插入、删除和查找操作的时间复杂度均为O(log n),这使得它们在处理大量数据时依然能够保持高效。
学习二叉搜索树和TreeSet/TreeMap的过程中,我认识到数据结构的选择对于程序的性能有着至关重要的影响。虽然HashMap在查找、插入和删除操作上提供了O(1)的时间复杂度,但是它不保证元素的顺序,而TreeSet和TreeMap在保持有序的同时,牺牲了一部分时间复杂度。在实际应用中,我们需要根据具体需求选择合适的数据结构,以达到最优的性能。
此外,在学习过程中,我也意识到了在多线程环境中使用TreeMap时需要注意同步问题。TreeMap不是线程安全的,如果需要在多线程环境中使用,需要程序员手动同步,或者通过包装等方式将TreeMap变成同步的。
总的来说,学习二叉搜索树和TreeSet/TreeMap让我对数据结构和算法有了更深入的理解,也让我认识到在实际编程中选择合适的数据结构的重要性。在未来的学习和工作中,我会继续探索和运用这些知识,以提高程序的性能和可靠性。
🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀
以上,就是本期的全部内容啦,若有错误疏忽希望各位大佬及时指出💐
制作不易,希望能对各位提供微小的帮助,可否留下你免费的赞呢🌸
