其实堆排序已经涉及到一个叫做“树”的数据结构了,它不同于链表、栈、队列等,它是一种非线性的数据结构。那么我们今天不说太多,后面自然会仔细讲解的,今天我们就学会一些基础的概念就行。
一、树结构
相信大家在数学中的求概率中都见过树状图,直到什么是树状图,这样的话,下面就直接上图了:

像这种,除了初始的节点外,每个节点都有且只有一个前驱节点,也可能会有多个后继节点的关系图就是树状图。
1.基本概念
下面引入一些概念:
父节点:又称双亲结点。某节点的前驱节点就是该节点的父节点。
子节点:又称孩子节点。某节点的后继节点就是该节点的子节点。
兄弟节点:父节点相同的两个或多个节点之间互称为兄弟节点。
节点的度:每个节点的子节点数目被称为该节点的度。像上图前两行的节点的度全部为3,也就是该节点拥有直接后继节点的数目。
叶节点:又称终端节点。度为0的节点被称为叶节点,也就是终端节点。
分支节点:又称非终端节点。度不为0的节点被称为非终端节点。
树的度:一棵树的度是所有节点中最大的度。
节点的层次:从根开始为第一层,往下每一个节点层数加一
树的高度(深度):层次的最大值就是树的高度
堂兄弟节点:父节点在同一层的节点且父节点不同的节点互为堂兄弟节点
节点的祖先:从某节点的线路一直向上遍历,遍历经过的所有节点都是该节点的祖先
子孙:某节点之下的所有子树的节点都是该节点的子孙。也就是该节点一直向下遍历,遇到分支分别遍历,经过的所有节点都是该节点的子孙。
森林:互不相交的n棵树(n>=2)组成的集合叫做森林
2.二叉树
如果树的度超过2会比较复杂难以研究。我们经常选取树的度为2的树作为研究对象。这类树又被称为二叉树。二叉树顾名思义,每个节点最多有两个分支。
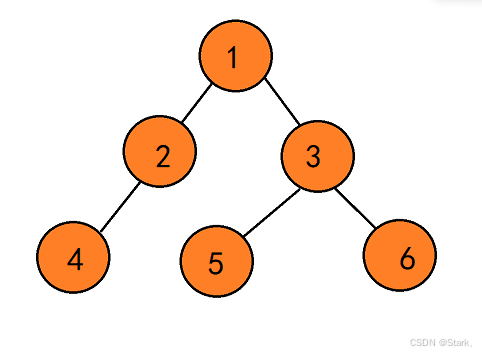
其中序号1为根节点。2和4所在分支为该树的左子树,3、5、6为该树的右子树。而2和3分别为1的左右子节点,5和6分别为3的左右子节点。但4是2的左节点?还是2的右节点?不知道,所以我们为了明确,下面引出特殊的二叉树:
3.特殊二叉树
特殊的二叉树分为完全二叉树和满二叉树。
满二叉树:除了最后一层的节点度全为0,其余节点的度都是2。这也就是满字的意义。二叉树决定了树的度上限为2,满字代表了节点的度全为2。但二叉树总归要有终端节点的,那就是最后一层的节点,而它们的度全为0。
完全二叉树:完全二叉树在满二叉树的基础上,允许倒数第二层的节点的度不全为0,但是最后一层从左到右的节点必须挨着。这样我们就可以直到度为1的节点的子节点必为该节点的左子节点。
4.二叉树的存储结构
二叉树的存储与其它线性结构类似,都有顺序存储和链式存储两种。但只是为了存储数据的话,我们为什么要用这么复杂的树形结构呢,线性结构存数据不香吗?
增删查改四大操作,二叉树的优势在于查找。存储只是一方面,查找才是二叉树的强项。
二叉树的物理结构是数组,逻辑结构是二叉树,真正实现的时候即使能用两种方式存储,大多数还是用数组存储数据的。接下来我们就开始讲一讲:堆。(这可不是内存的堆区空间的堆,而是一种特殊的数据结构)。
二、堆结构
1.堆的概念
堆就是用满二叉树实现的。堆又分为大根堆和小根堆。
大根堆:父节点永远大于子节点。根节点存储的就是该组数据的最大值。
小根堆:父节点永远小于子节点。根节点存储的就是改组数据的最小值。
2.堆的实现

调整子树
void adjust(vector<int>& v, int _begin, int _end) { int father = _begin;//传入的参数就是父节点 int child = father * 2 + 1;//左子下标 while (child <= _end) { if (child + 1 <= _end && v[child + 1] > v[child]) { child++; } if (v[child] > v[father]) { swap(v[child], v[father]); father = child; child = father * 2 + 1; } else break;//避免死循环 } return; }初始化堆
void initHeap(vector<int>& v) { int n = v.size(); for (int i = n / 2 - 1; i >= 0; i--) { int father = i; int child = father * 2 + 1;//左子下标 while (child <= n-1) { if (child + 1 <= n-1 && v[child + 1] > v[child]) { child++; } if (v[child] > v[father]) { swap(v[child], v[father]); father = child; child = father * 2 + 1; } else break;//避免死循环 } return; } } void initHeap(vector<int>& v) { int n=v.size(); for(int i=n/2-1;i>=0;i--){ adjust(v,i,n-1); } }三、堆排序
1.过程分析
第一步:将待排序数组形成一个堆结构,然后调整至最大堆
(堆结构:左孩子下标是2i+1,有孩子下标是2i+2)
(最大堆的特点:在这个堆结构中,任何一个父节点的值都大于其子节点的值)
第二步:将堆顶元素与待排序数组(假设待排序数组的元素个数为n)最后一个图元素进行交换
swap(&a[0],&a[n-1]);
第三步:待排序数据量减少一个:n--;将待排序数组重新调整最大堆结构,重复第二步,循环n-1次,将所有数据排序完成。
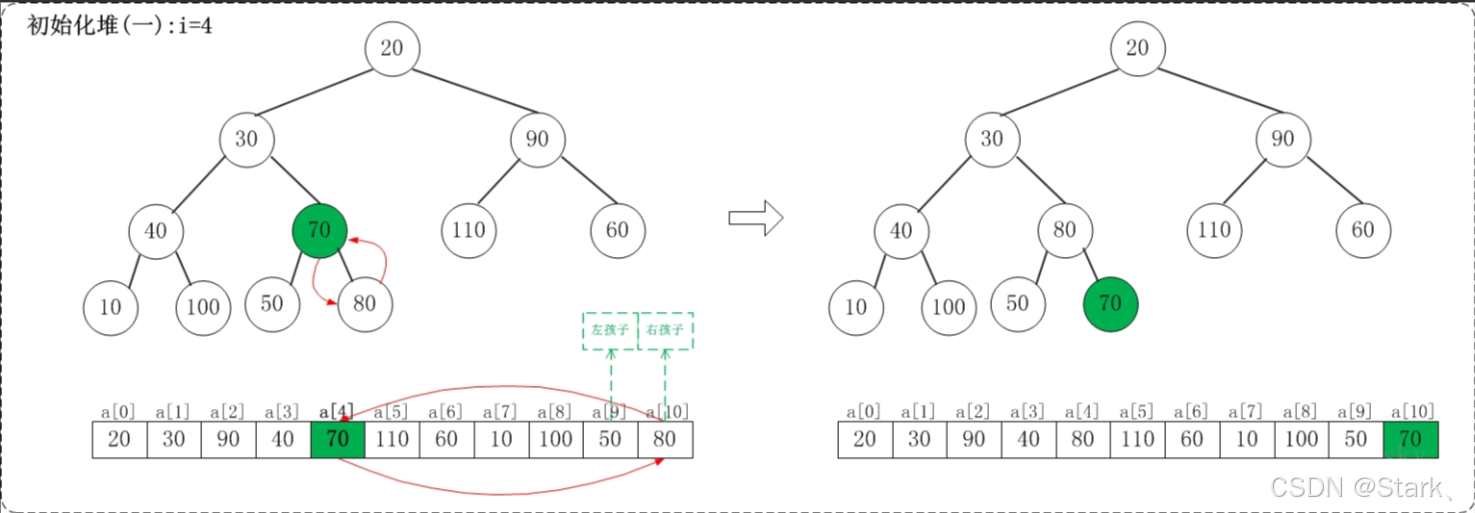
注意:初始化堆(将数组调整成最大堆)从最后一个父节点开始调整(即i=n/2-1)
下面演示数组{20,30,90,40,70,110,60,10,100,50,80}转化为最大堆{110,100,90,40,80,20,60,10,30,50,70}的步骤:





2.代码实现
void HeapSort(vector<int>& v) {//堆结构:完全二叉树 //初始化阶段:调整至最大堆结构(升序) //第一步:获取数组大小 int n = v.size(); //第二步:获取堆的最后一个父节点 int pos_last_parent = n / 2 - 1; //第三步:调整堆结构,从最后一个父节点一直到根节点 for (int i = pos_last_parent; i >= 0; i--) { adjust(v, i, n - 1); //对每一个部分堆进行调整,从第i个位置开始,到n-1处的最后一个元素结束 } //initHeap(v); //阶段结果:堆顶元素就是待排序的最大值 //排序阶段:交换最大值与待排序的尾元素 for (int i = n - 1; i >= 1; i--) { swap(v[0], v[i]);//交换值 adjust(v, 0, i - 1); //重新调整节点,从根节点0开始,到待排的最后一个元素i-1结束 } }3.算法分析
时间复杂度:O(nlogn)
稳定性:不稳定
