概念描述
栈是限定仅在表位进行插入或删除操作的线性表。栈的表尾称为栈顶,表头称为栈底。不含元素的栈称为空栈。
左图为栈的示意图,右图为用铁路调度表示栈。

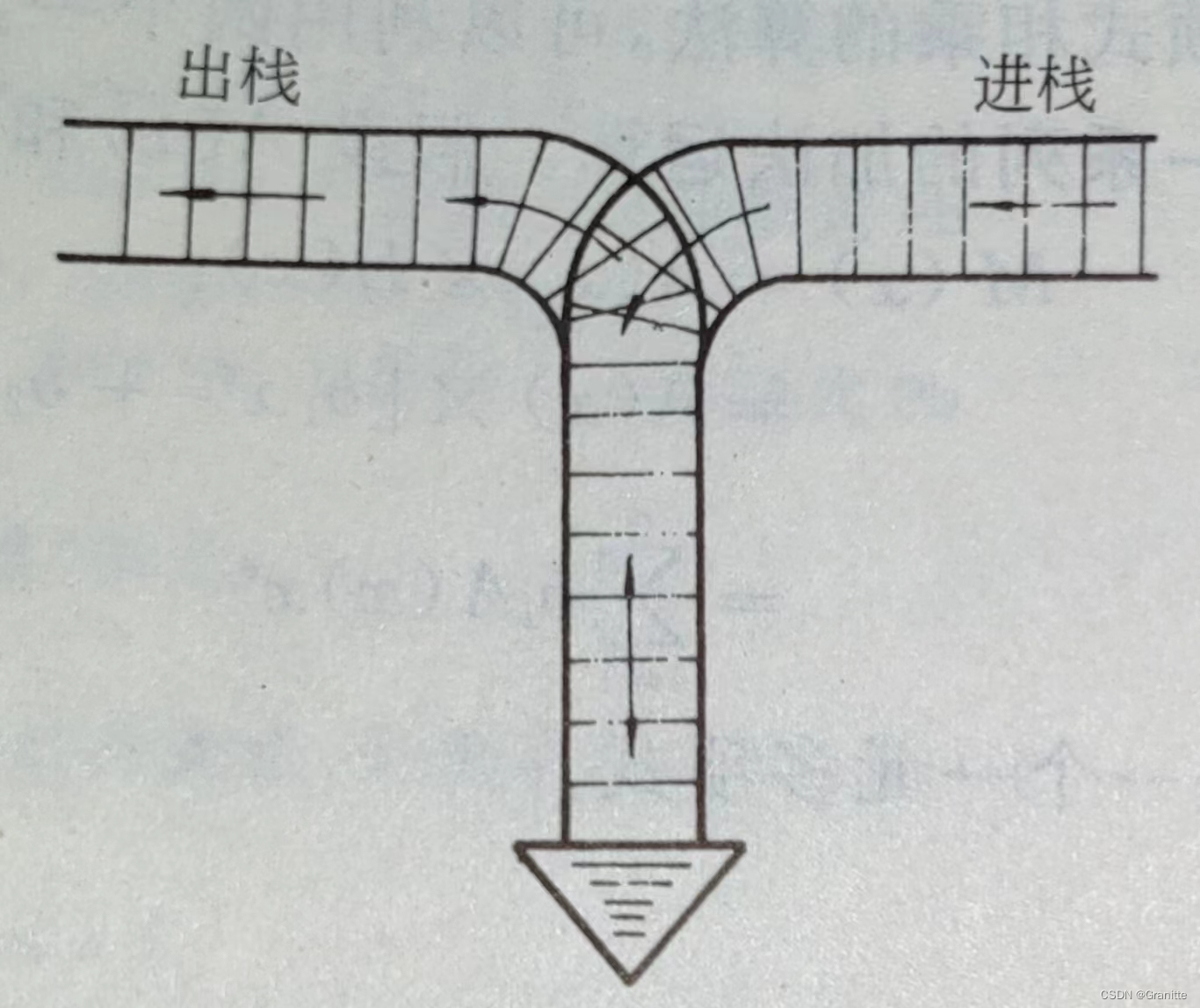
如下是入栈至栈满再进行出栈的过程示意图。值得注意的是,栈满后,top指针指向的不是顶端元素,而是顶端的下一个位置。

基本操作
构造一个空栈S
在正式开始前,照例需要定义一些如下的常量
#define STACK_INIT_SIZE 100//存储空间初始分配量 #define STACKINCREMENT 10//存储空间分配增量 #define TRUE 1 #define ERROR 0 #define OVERFLOW -2 typedef char SElemType; tyoedef int Status; typedef struct{ SElemType *base;//栈底指针.在栈构造之前和销毁之后,base的值为NULL SElemType *top;//栈顶指针 int stacksize;//当前已分配的存储空间,初始值一般为STACK_INIT_SIZE,不够时再以STACKINCREMENT为单位扩大 }SqStack;在顺序栈中,base指针始终指向栈底元素,栈不存在的条件为base=NULL。top指针初值指向栈底,栈空的条件为base==top。栈不空时,top指向(栈顶+1)。也就是说,在正常情况下,S.top 是不指向任何元素的。(top-base)的值即为栈中元素的个数,也即栈的长度。当top-base==stacksize时,说明栈满。此时若想进行入栈操作,需要扩充分配存储空间。
判空
Status StackEmpty(SqStack S) { if(!S.base) return TRUE; else return FALSE; }构造一个空栈
Status InitStack(SqStack &S) { S.base=(SElemType*)malloc(STACK_INIT_SIZE*sizeof(SElemType)); if(!S.base) exit(OVERFLOW); S.top=S.base; S.stacksize=STACK_INIT_SIZE; return OK; }若栈不存在,分配空间时发生上溢出错误而退出。
入栈
在入栈、出栈、取栈顶元素的函数中,不存在分配空间的问题,是return ERROR而不是 exit(OVERFLOW)
Status Push(SqStack& S, SEIemType e)//入栈 { if (S.top - S.base >= S.stacksize) return ERROR; *S.top = e;//注意S.top是指针型变量 S.top++;//先赋值,再加一 return OK; }出栈
Status (SqStack &S) { if(S.top==S.base) return ERROR; S.top--; e=*(S.top); return OK; }值得注意的是,出栈后,元素e并未从栈中删除。改变的只是top指针的位置。虽然e还在栈中,但栈长已经改变,e的原位置此后可以被其它值覆盖。

取栈顶元素
取栈顶元素就是“top指针位置不变”版的“出栈”。博主初学时没意识到这一点,以为出栈就是删除元素,所以构造了一个很复杂的取栈顶元素函数。为避免误导,就不放在这里了。
Status(SqStack S,SElemType) { if(S.top==S.base) return ERROR; e=*(S.top-1);//top指针位置不变 return OK; }输出栈中所有元素
和取栈顶元素同理,在不移动指针位置的情况下输出元素。若采用for循环,需要先求栈长。一般使用while循环。
Status PrintStack(SqStack S) { int i=0; SElemType *s; s=S.base;//注意!顺序栈从底部开始向上存储,顺序输出是从S.base开始 //并且,如果想做逆序输出,while循环条件应为s!=S.base-1 while(s!=S.top) { printf("%c\n",*s); s++; i++; } printf("已输出栈中%d个元素",i); return OK; }Status PrintStack(SqStack S) { int a=S.top-S.base; if(S.base==S.top) return ERROR; int i; for(i=1;i<=a;i++) printf("%c\n",*(S.top-a)); printf("已输出栈中%d个元素",a); return OK; }括号匹配
题干描述
由键盘输入一系列左括号和右括号,判断这些括号是否成功配对。一旦发现不配对的括号,立刻退出程序并说明原因。如:( { [ ] [ ] } )是匹配成功,而((]是由于括号不匹配而失败,{ ( [ ] )是因为左括号多余而失败,( { } ) ]是因为右括号多余而失败。
题目分析

代码(含分析)
Status March_Brackets(SqStack& S) { char ch;//输入一连串字符(括号),以回车结束.起初,括号都存储在ch中,栈S为空栈. SElemType* s; s = S.top-1;//s指向栈顶元素 printf("请输入字符:\n"); ch = getchar();//输入括号,进入循环 while (ch != '\n')//循环接收括号字符以回车为结束符,每输入一个括号,就进行一次判断。 { if (ch =='(' || ch == '[' || ch == '{') //如果ch是左括号,入栈.栈中存放左括号,有匹配的右括号就出栈.若全部匹配成功,栈空。 Push(S, ch); //入栈 if (ch == ')')//输入字符为右括号 { if ((Pop(S, *s) == 0)) { printf("右括号多余,不匹配\n"); return ERROR; } /*在Pop函数中, 若返回值为0, 说明是空栈.这有两种情况:1,还未输入左括号,第一个输入的就是右括号; 2,之前输入的左、右括号都已成功匹配,左括号已全部出栈*/ else if (*s != '(') { printf("右括号与左括号不匹配\n"); return ERROR; } /*最后输入的左括号不是小括号,与输入的右小括号不匹配*/ } else if (ch == ']') { if ((Pop(S, *s) == 0)) { printf("右括号多余,不匹配\n"); return ERROR; } else if (*s != '[') { printf("右括号与左括号不匹配\n"); return ERROR; } } else if (ch == '}') { if ((Pop(S, *s) == 0)) { printf("右括号多余,不匹配\n"); return ERROR; } else if (*s != '{') { printf("右括号与左括号不匹配\n"); return ERROR; } } ch = getchar(); }//循环结束,说明输入的右括号都有预支品牌的左括号.但这不意味着匹配成功!!还有左括号多余的可能。 if (S.top != S.base)//栈不空,说明有左括号未出栈,未匹配 { printf("左括号多余,不匹配\n"); return ERROR; } else//栈空,说明左括号已全部出栈,匹配成功 { printf("匹配完整,成功退出\n"); return OK; } } 上机实现
完整代码
经高手指点:由于getchar的一些特性,建议只执行一次括号判断函数。不要在主函数中反复执行它。
#include <stdio.h> #include <stdlib.h> typedef char SElemType; typedef int Status; constexpr auto ERROR = 0; constexpr auto OK = 1; constexpr auto OVERFLOW = -2; constexpr auto STACK_MAX_SIZE = 100; typedef struct { SElemType* base; SElemType* top; int stacksize; }SqStack; Status InitStack(SqStack& S)//建立空顺序栈 { S.stacksize = STACK_MAX_SIZE; S.base = (SElemType*)malloc(STACK_MAX_SIZE * sizeof(SElemType)); if (!S.base) exit(OVERFLOW); S.top = S.base; return OK; } Status Push(SqStack& S, SElemType e)//入栈 { if (S.top - S.base >= S.stacksize) exit(OVERFLOW); *S.top = e;//注意S.top是指针型变量 S.top++;//先赋值,再加一 return OK; } Status Pop(SqStack& S, SElemType& e)//出栈 { if (S.base == S.top) return ERROR; S.top--;//注意S.top是指针型变量 e = *S.top;//先减一,再赋值 return OK; } Status GetTop(SqStack S, SElemType &e)//获取栈顶元素 { if (S.top == S.base) return ERROR; e = *(S.top - 1);//top指针位置不变 return OK; } Status PrintStack(SqStack S)//输出栈所有元素 { if (S.top == S.base) return ERROR; int i = 0; SElemType* s; s = S.base; while (s != S.top) { printf("%c\n", *s); i++; s++; } printf("已输出栈中%d个元素", i); return OK; } Status March_Brackets(SqStack& S) { char ch;//输入一连串字符(括号),以回车结束.起初,括号都存储在ch中,栈S为空栈. SElemType* s; s = S.top-1;//s指向栈顶元素 printf("请输入字符:\n"); ch = getchar();//输入括号,进入循环 while (ch != '\n')//循环接收括号字符以回车为结束符,每输入一个括号,就进行一次判断。 { if (ch =='(' || ch == '[' || ch == '{') //如果ch是左括号,入栈.栈中存放左括号,有匹配的右括号就出栈.若全部匹配成功,栈空。 Push(S, ch); //入栈 if (ch == ')')//输入字符为右括号 { if ((Pop(S, *s) == 0)) { printf("右括号多余,不匹配\n"); return ERROR; } /*在Pop函数中, 若返回值为0, 说明是空栈.这有两种情况:1,还未输入左括号,第一个输入的就是右括号; 2,之前输入的左、右括号都已成功匹配,左括号已全部出栈*/ else if (*s != '(') { printf("右括号与左括号不匹配\n"); return ERROR; } /*最后输入的左括号不是小括号,与输入的右小括号不匹配*/ } else if (ch == ']') { if ((Pop(S, *s) == 0)) { printf("右括号多余,不匹配\n"); return ERROR; } else if (*s != '[') { printf("右括号与左括号不匹配\n"); return ERROR; } } else if (ch == '}') { if ((Pop(S, *s) == 0)) { printf("右括号多余,不匹配\n"); return ERROR; } else if (*s != '{') { printf("右括号与左括号不匹配\n"); return ERROR; } } ch = getchar(); }//循环结束,说明输入的右括号都有预支品牌的左括号.但这不意味着匹配成功!!还有左括号多余的可能。 if (S.top != S.base)//栈不空,说明有左括号未出栈,未匹配 { printf("左括号多余,不匹配\n"); return ERROR; } else//栈空,说明左括号已全部出栈,匹配成功 { printf("匹配完整,成功退出\n"); return OK; } } int main(void) { SqStack S; int i; char e; char f; char k; InitStack(S); printf("请向栈中输入字符\n"); for (i = 0; i < 7; i++) { scanf_s("%c", &e); Push(S, e);//入栈 } printf("已初始化栈如下\n"); PrintStack(S); GetTop(S, f);//获取栈顶元素 printf("栈顶元素为\n"); putchar(f); printf("删除栈顶元素\n"); Pop(S, k);//出栈 printf("更新栈如下\n"); PrintStack(S); printf("下面进入括号匹配\n"); SqStack B; InitStack(B); March_Brackets(B); return 0; }运行结果


