【OpenCV C++20 学习笔记】Sobel求导-边缘检测

Sobel求导-边缘检测

• 原理
• • Sobel算子
  • • 公式
    • Scharr算法
• API
• 实例

原理

图像中的边缘线是像素值显著变化的边界，而在数学上确定一个函数发生显著变化的位置的方法就是求导。
假设有一个1维的图片$f(t)$，在$t$处有颜色值的显著变化：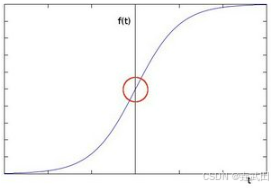

对$f(t)$求一阶导数$f^{\prime }(t)$，可以很轻易发现在相应位置的一个导数的最大值：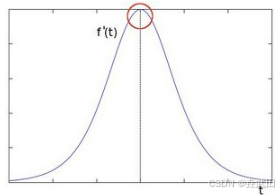

Sobel算子

• Sobel算子是一个离散微分算子，计算图片颜色值变化的近似斜率
• Sobel算子将高斯平滑和微分算法结合起来了

公式

设要被进行计算的图片为$I$，则：

1. 水平变化$G_x$可以通过将$I$和奇数方的卷积核进行卷积运算得到，比如，使用一个$3\times 3$的卷积核，可以算得：
   $$G_x=\left[\begin{array}{ccc}-1& 0& +1\\ -2& 0& +2\\ -1& 0& +1\end{array}\right]\ast I$$
2. 同样的，将这个卷积核逆时针旋转90度之后，再和$I$进行卷积运算，就可以得到垂直变化$G_y$：
   $$G_y=\left[\begin{array}{ccc}-1& -2& -1\\ 0& 0& 0\\ +1& +2& +1\end{array}\right]\ast I$$
3. 这样，近似斜率$G$就可以通过这两个方向上的变化求得：
   $$G=\sqrt{G_x^2+G_y^2}$$
   或者可以近似简化为：
   $$G=|G_x|+|G_y|$$

Scharr算法

当卷积核的尺寸较小的时候，比如$3\times 3$，Sobel计算出的斜率会很不精确，因为毕竟它只是对一个离散的对象进行近似求导。
OpenCV使用Scharr()函数来用$3\times 3$的卷积核进行近似求导，从而解决Sobel算法的不精确的问题。Scharr算法使用的卷积核如下：
$$G_x=\left[\begin{array}{ccc}-3& 0& +3\\ -10& 0& +10\\ -3& 0& +3\end{array}\right]$$
$$G_y=\left[\begin{array}{ccc}-3& -10& -3\\ 0& 0& 0\\ +3& +10& +3\end{array}\right]$$

API

Sobel函数的原型如下：

void cv::Sobel(	InputArray	src,						//输入图 				OutputArray	dst,						//输出图 				int			ddepth,						//输出图的数据类型 				int			dx,							//水平变化的顺序 				int			dy,							//垂直变化的顺序 				int			Ksize = 3,					//卷积核的尺寸，可以是1、3、5或7，默认为3 				double		scale = 1,					//对计算结果的放大系数，默认为1，即不放大 				double		delta = 0,					//对计算结果的偏移值，默认是0，即不偏移 				int			borderType = BORDER_DEFAULT)//图片边缘的扩充类型，不能是BORDER_WRAP，默认是镜像复制 

• dx、dy和Ksize三个参数共同决定了该方法所使用的卷积核：
  * 如果dx=1, dy=0, Ksize=3，那么就是上一张中的水平差异计算中使用的卷积核，即：
  $$\left[\begin{array}{ccc}-1& 0& +1\\ -2& 0& +2\\ -1& 0& +1\end{array}\right]$$
  * 如果dx=0, dy=1, Ksize=3，那么就是上一张中的水平差异计算中使用的卷积核，即：
  $$\left[\begin{array}{ccc}-1& -2& -1\\ 0& 0& 0\\ +1& +2& +1\end{array}\right]$$
• 如果Ksize= #FILTER_SCHARR(-1)，则表明使用Scharr算法。
• 当Ksize = 1时，该方法使用$1\times 3$或$3\times 1$的卷积核，因此没有高斯分布，而且只能用在求一阶或二阶导数的时候。

Scharr()函数的原型与Sobel()函数类似，只是没有了Ksize参数：

void cv::Scharr(InputArray	src, 				OutputArray	dst, 				int			ddepth, 				int			dx, 				int			dy, 				double		scale = 1, 				double		delta = 0, 				int			borderType = BORDER_DEFAULT) 

实例

在进行Sobel计算之前，需要先减少图片中的噪音，可以使用高斯平滑：

Mat blured; GaussianBlur(src, blured, Size(3, 3), 0, 0, BORDER_DEFAULT); 

然后进行灰度化，以便更好地显示边缘线：

Mat gray; cvtColor(blured, gray, COLOR_BGR2GRAY); 

接着，分别计算水平差异和垂直差异（都使用$3\times 3$的卷积核）：

Mat Gx, Gy; Sobel(gray, Gx, -1, 1, 0, 3, 1, 0, BORDER_DEFAULT); Sobel(gray, Gy, -1, 0, 1, 3, 1, 0, BORDER_DEFAULT); 

这样就可以计算近似斜率了，这里使用了简化的算法，即它们绝对值的和：

//取绝对值 Mat abs_Gx, abs_Gy; convertScaleAbs(Gx, abs_Gx); convertScaleAbs(Gy, abs_Gy); //计算近似斜率 Mat G; addWeighted(abs_Gx, 0.5, abs_Gy, 0.5, 0, G); 

这样就完成了整个边缘检测的过程。
我们还计算了Scharr算法下的结果，它们之间的对比如下（从左到右分别为原图、Soble和Scharr）：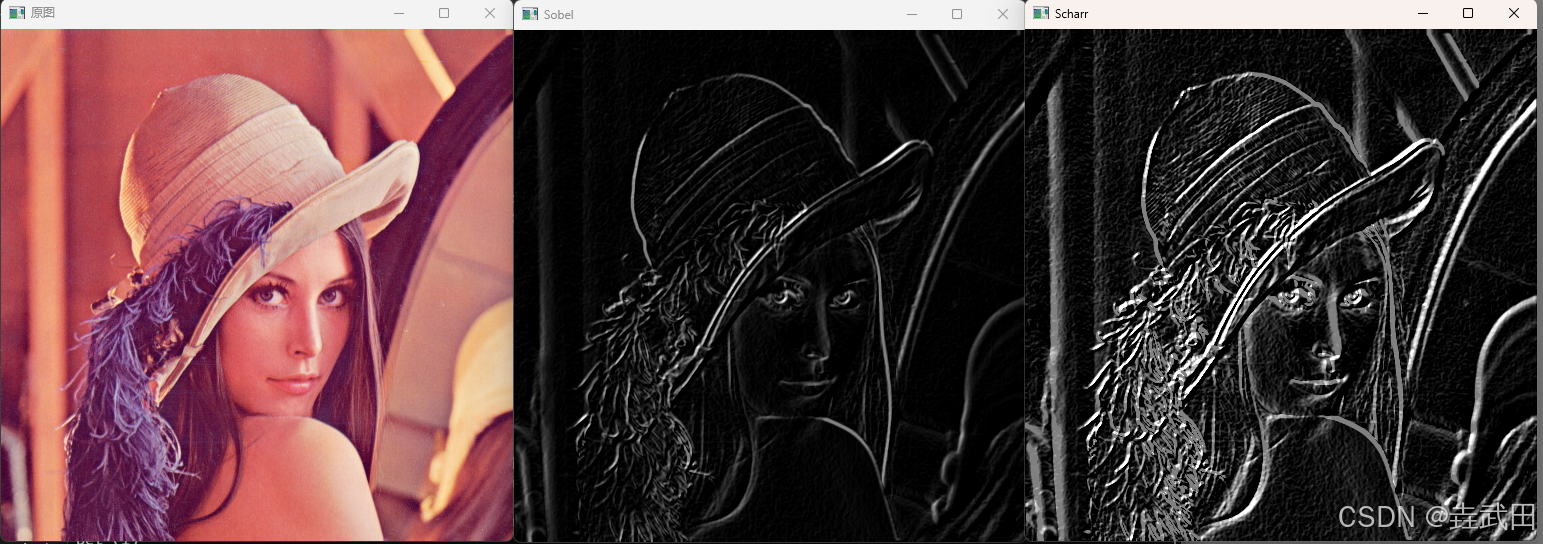

可以看到，在卷积核是$3\times 3$的情况下，Scharr算法得出的结果细节更丰富。