阅读量:0
✨✨欢迎大家来到Celia的博客✨✨
🎉🎉创作不易,请点赞关注,多多支持哦🎉🎉
所属专栏:排序
一、快速排序的思想
快速排序的核心思想是:
- 选定一个key值作为基准值(一般是整个数组的第一个元素)。
- 把整个数组中比key小的元素放到key的左边,比key大的元素放到key的右边。这需要通过一次单趟排序来实现。
- 单趟排序结束后,可以认为先前选定的key值的位置已经排好序了。根据这个key值的位置,将数组分为左右两个子数组,再分别进行单趟排序(重复2过程)。直到左右数组不能再分为止。
二、快速排序的原理分析
想要实现快速排序,最重要的就是实现单趟排序,单趟排序主要有三个方法:霍尔法、挖坑法、前后针法。
2.1 霍尔法
霍尔法的思想是:
- 定义左右两个指针分别指向当前数组的首尾两边。
- 让右指针先走,从右往左找到首个比key值小的元素。
- 再让左指针走,从左往右找到首个比key值大的元素。
- 交换左右指针所指向的两个元素。
- 重复2、3步骤,直到左右指针相遇。
- 将key值所在的位置与左右指针相遇的位置的元素交换。
- 单趟排序结束,key值所在的位置左边都比key值小,右边都比key值大。

还有一个很重要的问题,为什么在单趟排序之后,两个指针相遇位置的元素值一定比key小呢?
- 如果左指针遇到右指针,由于右指针是先走的,说明右指针已经找到了比key小的元素。
- 如果右指针遇到左指针,由于上一轮的交换,比key小的元素已经换到了当前左指针的位置,左指针的位置的元素一定也比key小。
结论:如果使用霍尔法进行单趟排序,只需要让与基准值(key)所在方位相反的指针先走就可以了。
2.2 挖坑法
挖坑法的思想是:
- 定义左右两个指针,分别指向数组的首尾位置。
- 选定一个基准值key(一般是数组的第一个元素),并记录。将当前基准值位置记作“坑”。
- 右指针先走,从右往左找到比key值小的元素。
- 将右指针所在的位置的元素移动到“坑”中,当前右指针所在的位置形成新的“坑”。
- 左指针再走,从左往右找到比key值大的元素。
- 将左指针所在的位置的元素移动到“坑”中,当前左指针所在的位置形成新的“坑”。
- 当左右指针相遇时,将key值填入左右指针相遇的位置。单趟排序结束。

这个方法相比于霍尔法更好理解,也不用考虑两指针相遇时的元素是否小于key的问题。 该方法效率与霍尔法相同。
2.3 前后指针法
前后指针法的思想是:
- 选定一个基准值,用key保存起来。
- 定义prev指针指向数组首位置,定义cur指向prev的下一个位置。
- 比较cur位置的元素与key的大小关系,若cur位置元素比key大,cur++。若cur位置元素比key小,先让prev++,再交换cur和prev位置的元素。
- 当cur大于数组大小时,结束遍历,将key所在的位置的值和prev所在位置的值交换。

三、快速排序的代码实现
3.0 核心代码逻辑
void Swap(int* a, int* b) { int tmp = *a; *a = *b; *b = tmp; } void QSort(int* a, int left, int right) { if (left >= right)//递归结束条件 return; int begin = left, end = right; //使用三种方法的其中一种进行单趟排序 int mid = Part3(a, begin, end);//记录每一次排好的元素下标 QSort(a, begin, mid - 1);//递归左右子数组 QSort(a, mid + 1, end); }递归调用会将整个数组不断地分为两个子数组,如果递归传入的left和right相等,不用进行排序,如果left大于right,不符合区间的逻辑,也不需要排序。所以递归的结束条件为 left >= right。
3.1 霍尔法
//霍尔法 int Part1(int* a, int left, int right) { int keyi = left; int begin = left, end = right; while (begin < end) { while (begin < end && a[end] >= a[keyi]) { end--; } while (begin < end && a[begin] <= a[keyi]) { begin++; } Swap(&a[begin], &a[end]); } Swap(&a[keyi], &a[begin]); return begin; }3.2 挖坑法
//挖坑法 int Part2(int* a, int left, int right) { int key = a[left]; int hole = left; int begin = left, end = right; while (begin < end) { while (begin < end && a[end] >= key) { end--; } a[hole] = a[end]; hole = end; while (begin < end && a[begin] <= key) { begin++; } a[hole] = a[begin]; hole = begin; } a[hole] = key; return hole; }3.3 前后指针法
//前后指针法 int Part3(int* a, int left, int right) { int keyi = left; int prev = left; int cur = prev + 1; while (cur <= right) { if (a[cur] <= a[keyi]) { prev++; Swap(&a[cur], &a[prev]); } cur++; } Swap(&a[keyi], &a[prev]); return prev; }四、快速排序的时间复杂度和空间复杂度分析
4.1 时间复杂度
- 快速排序最核心的步骤是对每个子数组进行遍历比较操作,所以我们用遍历的次数来近似时间复杂度。
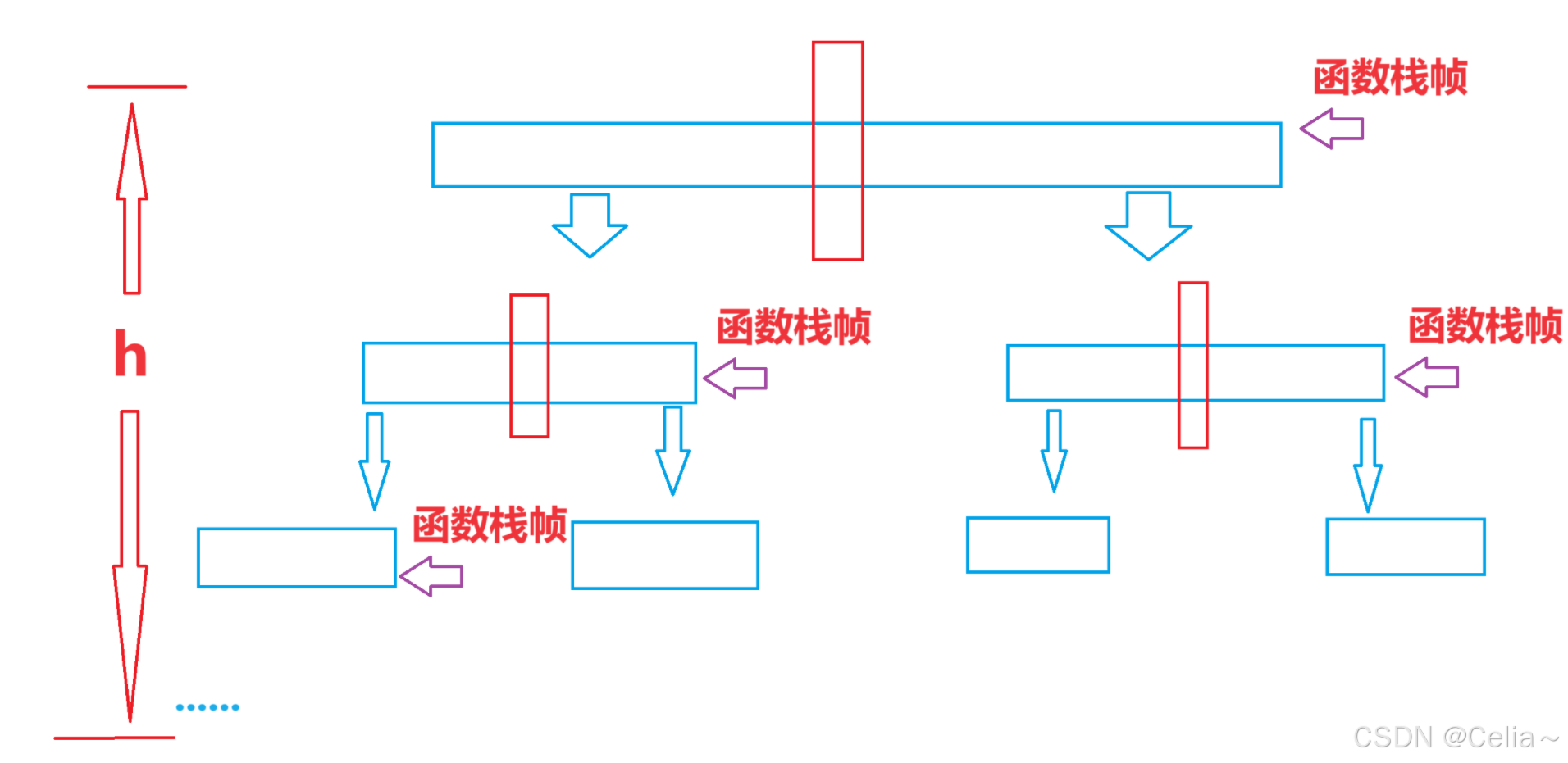
- 快速排序对数组的分组类似于二叉树,我们可以简易的把快速排序的层数(递归深度)设为h(类比二叉树深度),递归创建的总函数栈帧次数设为N(类比二叉树节点个数)。
- 则存在近似关系:
 ,则共有
,则共有  层,每一层的每一个节点都要遍历数组,整个一层加起来的遍历次数近似
层,每一层的每一个节点都要遍历数组,整个一层加起来的遍历次数近似 ,则总遍历次数为
,则总遍历次数为 。
。 - 则快速排序的时间复杂度为
 。
。
4.2 空间复杂度
- 快速排序所占用的额外空间主要为递归创建的函数栈帧,则空间复杂度就是递归创建的最大栈帧数量。由于栈的空间可以重复利用,则计算递归的最大深度即可,最大深度为:
 。
。 - 快速排序的空间复杂度为:
 。
。
五、快速排序的优化
- 快速排序在最好情况下可以看作一个完全二叉树,时间复杂度为
 。但是如果排序数组有序,那么每次把数组首位置作为基准位置的话,每次排序就相当于将数组分为 1 和 N - 1 个元素。每次排好一个元素,那么递归的深度就会大大增加。
。但是如果排序数组有序,那么每次把数组首位置作为基准位置的话,每次排序就相当于将数组分为 1 和 N - 1 个元素。每次排好一个元素,那么递归的深度就会大大增加。

- 遍历的总数就会变成一个等差数列,n + n - 1 + n - 2 + ... + 2 + 1,用求和公式求出结果后,最大的次方项变成了
 ,这不仅仅严重降低了效率,也有可能会因为递归层数太深造成栈溢出的风险。
,这不仅仅严重降低了效率,也有可能会因为递归层数太深造成栈溢出的风险。 - 为了解决这两个问题,可以使用三数取中和小区间优化来解决这些问题。
5.1 三数取中
- 三数取中的思想是,取数组首、末、中三个位置的值,记录这三个位置上大小为中间值的下标。并将这个取中的值与数组首元素交换。这样一来,以首尾值为基准值,基准值最终排好的位置会趋近于数组中间,就会将数组尽可能分为长度大致相等的两部分进行递归,以增加效率和减少递归深度。
//三数取中 int FindMid(int* a, int left, int right) { int mid = (left + right) >> 1; if (a[left] < a[mid]) { if (a[mid] < a[right]) return mid; else //a[mid] >= a[right] mid最大,选left和right中最大的 { if (a[left] > a[right]) return left; else return right; } } else //a[left] >= a[mid] { if (a[mid] > a[right]) return mid; else //a[mid] <= a[right] mid最小,选left和right中最小的 { if (a[right] < a[left]) return right; else return left; } } }- 加入了三数取中,快速排序的核心代码就变成了:
void QSort(int* a, int left, int right) { if (left >= right) return; int begin = left, end = right; int middle = FindMid(a, left, right); Swap(&a[left], &a[middle]);//交换 int mid = Part3(a, begin, end); QSort(a, begin, mid - 1); QSort(a, mid + 1, end); }5.2 小区间优化
- 小区间优化主要是针对排序数组的元素数量较少时,进行递归开辟函数栈帧开销太大(就是没有必要),不如使用其他的排序算法(快一些,但不额外开辟空间)来进行排序。一般情况下,小区间优化使用的排序算法为插入排序。
//插入排序 void InsertSort(int* a, int n) { for (int i = 0; i < n - 1; i++) { int end = i; int tmp = a[end + 1]; while (end >= 0) { if (tmp < a[end]) { a[end + 1] = a[end]; end--; } else break; } a[end + 1] = tmp; } }- 快速排序的主要逻辑变为:
void QSort(int* a, int left, int right) { if (left >= right) return; if (right - left + 1 < 10) { InsertSort(a + left, right - left + 1);//插入排序 } else { int begin = left, end = right; int middle = FindMid(a, left, right); Swap(&a[left], &a[middle]);//交换 int mid = Part3(a, begin, end); QSort(a, begin, mid - 1); QSort(a, mid + 1, end); } }- 这里需要注意,由于递归进行到一定深度时,数组区间元素个数较少的情况下([left, right]),排序的区间是整个数组的一小段,故插入排序传入的首地址需要传 a + left,排序元素数量需要传right - left + 1。

