机器学习第八章——集成学习_业界新闻

发布时间:2024-08-07 10:05

阅读量:0

一、个体与集成

集成学习(ensemble learning)通过构建并结合多个学习器来完成学习任务，有时也被称为多分类器系统(multi-classifier system)、基于委员会的学习(committee-based learning)等.

集成学习的一般结构：

同质集成：只包含同种类型的个体学习器，“基学习器”(base learner),相应的学习算法称为“基学习算法”(base learning algorithm)。
异质集成：包含不同类型的个体学习器，“组件学习器”(component learner)或直接称为个体学习器。

集成学习通过将多个学习器进行结合,常可获得比单一学习器显著优越的泛化性能.

考虑一个简单的例子:在二分类任务中,假定三个分类器在三个测试样本上的表现如下图所示,其中√表示分类正确,×表示分类错误,集成学习的结果通过投票法(voting)产生，即“少数服从多数”．

要获得好的集成，个体学习器应“好而不同”,即个体学习器要有一定的“准确性”，即学习器不能太坏，并且要有“多样性”(diversity)，即学习器间具有差异.

假设学习器的误差相互独立，则随着集成中个体分类器数目的增大,集成的错误率将指数级下降,最终趋向于零（但现实生活中不可能独立）。

根据个体学习器的生成方式，目前的集成学习方法大致可分为两大类,即

个体学习器间存在强依赖关系、必须串行生成的序列化方法：Boosting
个体学习器间不存在强依赖关系、可同时生成的并行化方法：Bagging 和“随机森林”(Random Forest).

二、Boosting

Boosting的工作机制类似:先从初始训练集训练出一个基学习器,再根据基学习器的表现对训练样本分布进行调整,使得先前基学习器做错的训练样本在后续受到更多关注，然后基于调整后的样本分布来训练下一个基学习器;如此重复进行,直至基学习器数目达到事先指定的值T,最终将这T个基学习器进行加权结合。

Boosting族算法最著名的代表是AdaBoost,其描述如下图所示,其中 $y_{i}\in \left \{ -1,+1 \right \}$ ,是真实函数。

AdaBoost 算法有多种推导方式，比较容易理解的是基于“加性模型”(additive model)，即基学习器的线性组合

$H(x)=\sum_{t=1}^{T}\alpha _{t}h_{t}(x)$

来最小化指数损失函数(exponential loss function)

$l_{exp}(H\mid \mathcal D)=\mathbb{E}_{X\sim \mathcal D}[E^{-f(x)H(x)}]$

若H(a)能令指数损失函数最小化,则考虑上式对H(x)的偏导

因此，有

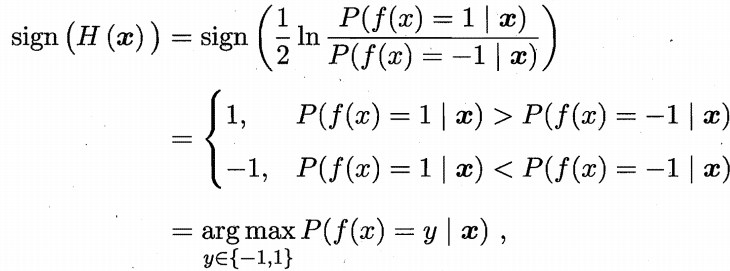
这意味着达到了贝叶斯最优错误率.换言之,若指数损失函数最小化,则分类错误率也将最小化;这说明指数损失函数是分类任务原本0/1损失·函数的一致的(consistent)替代损失函数．

使用Python和scikit-learn库实现的AdaBoost算法:

# 导入所需的库和数据集 from sklearn.ensemble import AdaBoostClassifier from sklearn.tree import DecisionTreeClassifier from sklearn.svm import SVC from sklearn.datasets import load_iris from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score  # 加载数据集 data = load_iris() X, y = data.data, data.target  # 将数据集分为训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)  # 初始化AdaBoost算法，并使用两种不同的基本分类器 base_estimators = [     DecisionTreeClassifier(max_depth=1),  # 使用深度为1的决策树作为第一个基本分类器     SVC(kernel='linear', C=1.0)          # 使用线性SVM作为第二个基本分类器 ] n_estimators = 50                        # 设置迭代次数为50 learning_rate = 1.0                      # 设置学习率为1.0 #使用AdaBoost算法创建分类器对象clf，estimator参数指定使用的基本分类器，这里选择使用base_estimators列表中的第一个元素，即深 #度为1的决策树 clf = AdaBoostClassifier(estimator=base_estimators[0], n_estimators=n_estimators, learning_rate=learning_rate)  # 在训练集上拟合模型 clf.fit(X_train, y_train)  # 在测试集上评估模型 y_pred = clf.predict(X_test) accuracy = accuracy_score(y_test, y_pred) print("Accuracy: %.2f%%" % (accuracy * 100.0))

三、Bagging与随机森林

1、Bagging

Bagging是并行式集成学习方法最著名的代表.直接基于自助采样法 (bootstrap sampling).给定包含m个样本的数据集,随机取出一个样本放入采样集中，再把该样本放回初始数据集,经过m次随机采样操作.
可采样出T个含m个训练样本的采样集,然后基于每个采样集训练出一个基学习器，再将这些基学习器进行结合.

Bagging 通常对分类任务使用简单投票法，对回归任务使用简单平均法.

没有被采用过的样本可用作验证集来对泛化性能进行“包外估计”(out-of-bag estimate) .需记录每个基学习器所使用的训练样本.

不妨令 $D_{t}$ 表示 $h_{t}$ 实际使用的训练样本集,令 $H^{oob}(x)$ 表示对样本的包外预测,有

则Bagging泛化误差的包外估计为

包外样本的其他用途：决策树：助剪枝、估计后验概率，神经网络：辅助早停

2、随机森林

随机森林(Random Forest，简称RF) 在以决策树为基学习器构建Bagging集成的基础上，进一步在决策树的训练过程中引入了随机属性选择。

在RF中，对基决策树的每个结点,先从该结点的属性集合中随机选择一个包含k个属性的子集,然后再从这个子集中选择一个最优属性用于划分.推荐值 $k=\log _{2}d$ 。

随机森林简单、容易实现、计算开销小，基学习器的多样性不仅来自样本扰动,还来自属性扰动。

随机森林的收敛性与 Bagging 相似.起始性能往往相对较差,随着个体学习器数目的增加，随机森林通常会收敛到更低的泛化误差.

四、结合策略

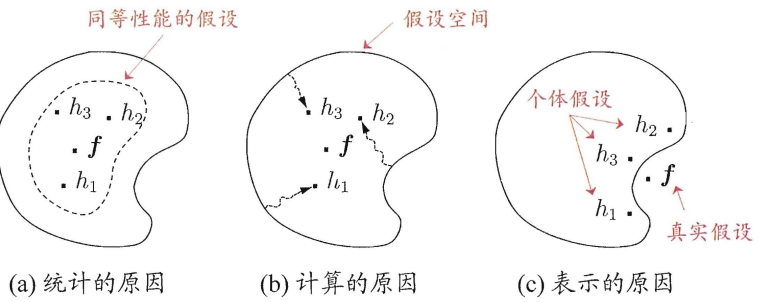
学习器结合可能会从三个方面带来好处:

统计：若使用单学习器可能因误选而导致泛化性能不佳,结合多个学习器则会减小这一风险;
计算：降低陷入糟糕局部极小点的风险
表示：假设空间有所扩大,有可能学得更好的近似.

1、平均法

简单平均法(simple averaging)： $H(x)=\frac{1}{T}\sum_{i=1}^{T}h_{i}(x)$ ，个体学习器性能相近时宜用。
加权平均法(weighted averaging)： $H(x)=\sum_{i=1}^{T}w_{i}h_{i}(x)$ ，通常要求 $w_{i}\geqslant 0,\sum_{i=1}^{T}w_{i}=1$ ，个体学习器性能相差较大时宜用，权重一般是从训练数据中学习而得。

2、投票法

绝对多数投票法(majority voting)：某标记得票数过半
相对多数投票法(plurality voting)：得票最多的标记
加权投票法(weighted voting)：

在现实任务中，不同类型个体学习器可能产生不同类型的 $h_{i}^{j}(x)$ 值，常见的有:

类标记: $h_{i}^{j}(x)\in \left \{ 0,1 \right \}$ ,若 $h_{i}$ 将样本预测为类别 $c_{j}$ 则取值为1，否则为0.使用类标记的投票亦称“硬投票”(hard voting).
类概率: $h_{i}^{j}(x)\in[0,1]$ ,相当于对后验概率 $P(c_{j} | x)$ 的一个估计.使用类概率的投票亦称“软投票”(soft voting).

不同类型的 $h_{i}^{j}(x)$ 值不能混用.对一些能在预测出类别标记的同时产生分类置信度的学习器,其分类置信度可转化为类概率使用．若此类值未进行规范化，进行“校准”(calibration)后才能作为类概率使用．若基学习器的类型不同,则其类概率值不能直接进行比较;在此种情形下,通常可将类概率输出转化为类标记输出(例如将类概率输出最大的h(ac)设为1,其他设为0)然后再投票.

3学习法

“学习法”：通过另一个学习器来进行结合.个体学习器称为初级学习器，用于结合的学习器称为次级学习器或元学习器(meta-learner)。

Stacking 先从初始数据集训练出初级学习器,然后“生成”一个新数据集用于训练次级学习器.初级集成是异质的。

一般是通过使用交叉验证或留一法这样的方式，用训练初级学习器未使用的样本来产生次级学习器的训练样本。

将初级学习器的输出类概率作为次级学习器的输入属性,用多响应线性回归(Multi-response Linear Regression,简称MLR)作为次级学习算法效果较好，在 MLR中使用不同的属性集更佳。

五、多样性

1、误差-分歧分解

假定我们用个体学习器 $h_{1},h_{2},...,h_{T}$ 通过加权平均法结合产生的集成来完成回归学习任务 $f :\mathbb{R}^{d} \mapsto \mathbb{R}$ 对示例x，定义学习器 $h_{i}$ 的“分歧”(ambiguity)为

则集成的“分歧”是:

这里的“分歧”项表征了个体学习器在样本。上的不一致性，即在定程度上反映了个体学习器的多样性。

2、多样性度量

多样性度量(diversity measure)是用于度量集成中个体分类器的多样性,典型做法是考虑个体分类器的两两相似/不相似性.

给定数据集 $D=\left \{ (x_{1},y_{1}) ,(x_{2},y_{2}) ,...,(x_{m},y_{m}) \right \}$ ，对二分类任务, $y_{i}\in \left \{ -1,+1 \right \}$ ,分类器 $h_{i}$ 与 $h_{j}$ 的预测结果列联表(contingency table)为

不合度量(disagreement measure) $dis_{ij}=\frac{b+c}{m}$ 值域为[0,1]，值越大多样性越大
相关系数(correlation coefficient)值域为[-1,1]，两者无关为0，正相关为正;
Q-统计量(Q-statistic) $Q_{ij}=\frac{ad-bc}{ad+bc}$
-统计量(r-statistic) $k=\frac{p_{1}-p_{2}}{1-p_{2}}$

k-误差图是将每一对分类器作为图上的一个点，横坐标为分类器的k值，纵坐标为平均误差。

3、多样性增强

一般思路是在学习过程中引入随机性，常见做法：

数据样本扰动：给定初始数据集,可从中产生出不同的数据子集,再利用不同的数据子集训练出不同的个体学习器。
基于采样法,（Bagging：自助采样，在AdaBoost：序列采样）。
对“不稳定基学习器”（如决策树、神经网络等）很有效；
“稳定基学习器”(stablebase learner)（如线性学习器、支持向量机、朴素贝叶斯、k近邻学习器等）不敏感。