文章目录
根据机械臂与相机所处的相对位置关系,一般分为 Eye-to-Hand 与 Eye-in-Hand 两种视觉系统。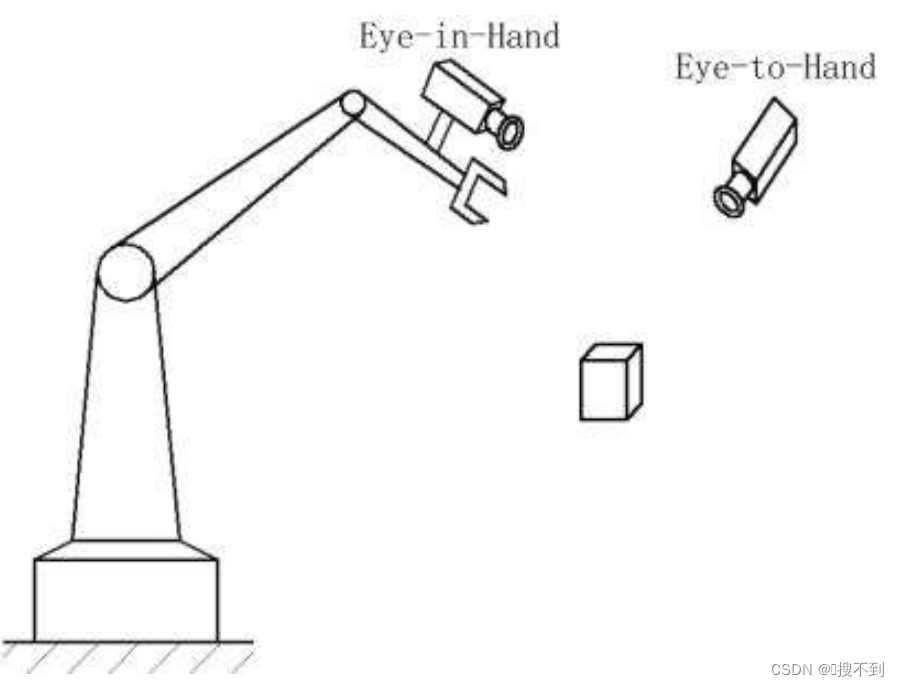
Eye-to-Hand
Eye-to-Hand 型机械臂视觉系统指的是相机固定安装于机械臂外,不随机械臂运动,与机械臂的基坐标系相对位置关系不变。
Eye-to-Hand 型机械臂视觉系统较为简单,其只需要对相机进行标定,即能确定相机坐标系与机械臂坐标系之间的变换关系,且因相机安装于机械臂外,不受机械臂振动等因素影响,精度能得到较好的保证。但其受限于安装位置,若要进行多次定位目标,则需要安装多台相机进行定位,大大增加了成本,若定位目标处空间狭小,无合适位置安装相机,同样也不适用。
Eye-in-Hand
Eye-in-Hand 型机械臂视觉系统则指的是相机安装在机械臂的末端执行器上,跟随末端执行器一起运动。
Eye-in-Hand 型机械臂视觉系统标定时,需要先对相机进行标定,再确定相机与机械臂末端的变换关系(即手眼标定),同时还需要对机械臂进行运动学分析,以确定相机坐标系在机械臂运动过程中的变换关系,较为复杂,但能较好地应对复杂多变的定位目标需求。
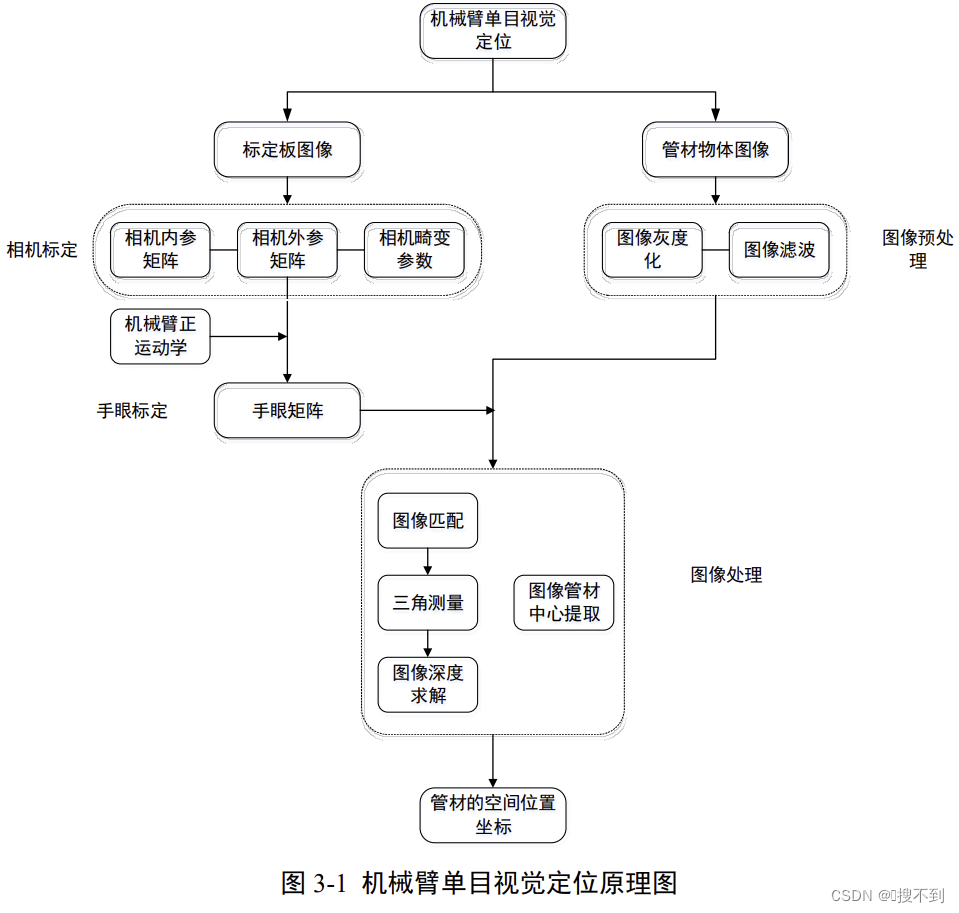
基于Eye-in-Hand型机械臂单目视觉定位
- 进行图像采集;以标定板图像通过相机标定与手眼标定,确定视觉系统的相机内外参数以及机械臂手眼矩阵;
- 对目标图像进行图像灰度化与图像滤波,去除图像的噪声,得到质量更高的处理图片;
- 对预处理后的一组图像进行图像匹配,基于三角测量原理,求取图像中特征点的深度信息;
- 对预处理后的图像进行图像轮廓提取,获取目标在图像中的位姿;
- 经坐标变换后确定目标在机械臂坐标系下的位姿。
单目相机标定
相机标定:根据相机成像模型求取相机的内部参数和外部参数。
针孔相机模型
- 相机内参矩阵
在理想的情况下,相机成像可简化为针孔成像: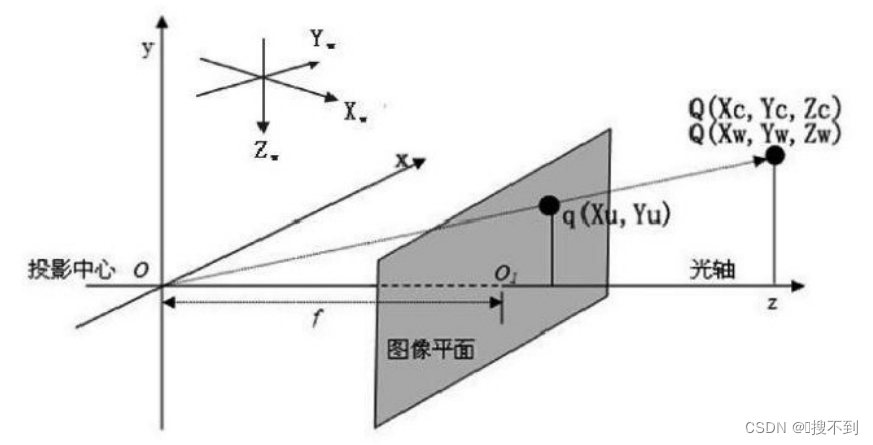
点 O O O是相机的光心,为相机坐标系的原点;点 O 1 O_1 O1是相机光轴与图像平面的交点,为图像平面的中心;空间中某点 Q Q Q在相机坐标系与世界坐标系的坐标分别为 ( X c , Y c , Z c ) (X_c,Y_c,Z_c) (Xc,Yc,Zc)和 ( X w , Y w , Z w ) (X_w,Y_w,Z_w) (Xw,Yw,Zw);点 q q q为 Q Q Q经成像投影后所得,在图像坐标系下的坐标为 ( X u , Y u ) (X_u,Y_u) (Xu,Yu); f f f为相机焦距,表示光心 O O O到图像平面的距离。
由相似三角形原理,可以得到:
{ X u f = X c Z c ⇒ X u = f X c Z c Y u f = Y c Z c ⇒ Y u = f Y c Z c \begin{cases}\dfrac{X_u}{f}=\dfrac{X_c}{Z_c}\Rightarrow X_u=f\dfrac{X_c}{Z_c}\\\dfrac{Y_u}{f}=\dfrac{Y_c}{Z_c}\Rightarrow Y_u=f\dfrac{Y_c}{Z_c}\end{cases} ⎩⎨⎧fXu=ZcXc⇒Xu=fZcXcfYu=ZcYc⇒Yu=fZcYc
通常,图像坐标系的原点不是相机光轴与图像平面的交点 O 1 O_1 O1,而是在图像的右上角,且与成像平面还存在一个缩放变换。
设 O 1 O_1 O1与图像坐标系原点的偏移量为 ( X 0 , Y 0 ) (X_0,Y_0) (X0,Y0),图像坐标系与成像平面在 X 轴与 Y 轴方向的缩放倍数分别为 f x f_x fx与 f y f_y fy:
{ X u = f x X c Z c + X 0 Y u = f y Y c Z c + Y 0 \begin{cases}X_u=f_x \dfrac{X_c}{Z_c}+X_0\\\\Y_u=f_y \dfrac{Y_c}{Z_c}+Y_0\end{cases} ⎩⎨
