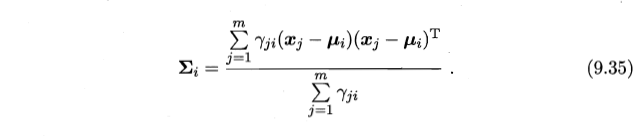阅读量:0
机器学习西瓜书学习笔记【第九章】
第九章 聚类
9.1 聚类任务
簇:给定一组数据点,我们可以使用聚类算法将每个数据点划分为一个特定的组。
9.2 性能度量
两类指标
外部指标:将聚类结果与某个"参考模 型" 进行比较
Jaccard 系数
FM指数
Rand指数

内部指标:直接考察聚类结果而不利用任何参考模型
DB指数
Dunn指数(DI)

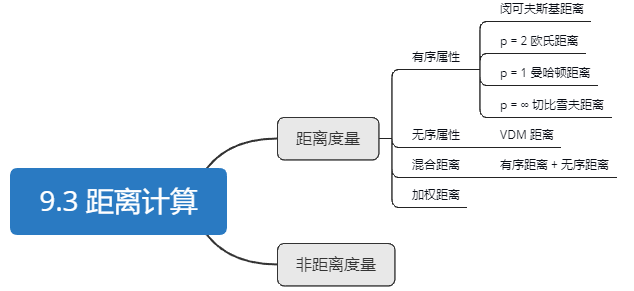
9.3距离计算
基本性质
非负性
统一性
对称性
直递性
属性
有序属性

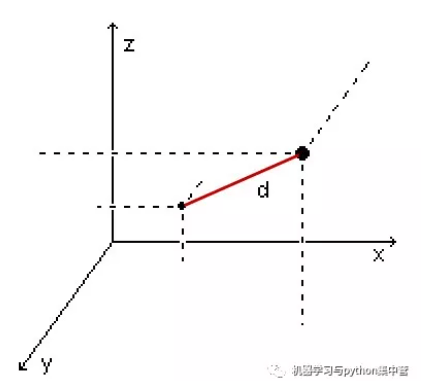
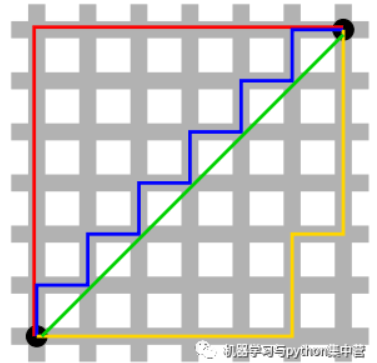
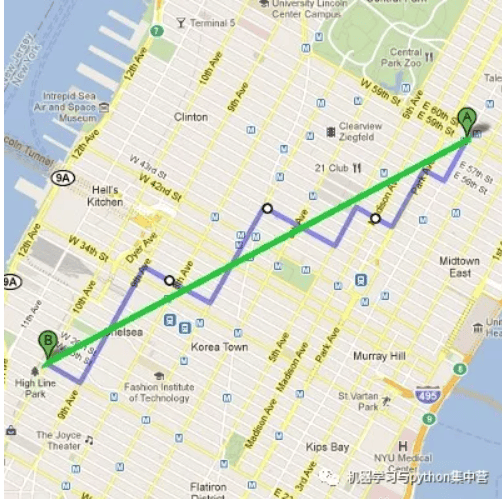
- 欧氏距离:
- 曼哈顿距离:
- 切比雪夫距离:
无序属性

混合距离
加权距离
9.4 原型聚类
K-MEANS聚类算法
步骤
①我们选择一些类/组来使用并随机地初始化它们各自的中心点。
②每个数据点通过计算点和每个组中心之间的距离进行分类,然后将这个点分类为最接近它的组。
③基于这些分类点,我们通过取组中所有向量的均值来重新计算组中心。
④对一组迭代重复这些步骤。
优势
速度非常快
劣势
①必须选择有多少组/类。
②从随机选择的聚类中心开始,因此在不同的算法运行中可能产生不同的聚类结果。因此,结果可能是不可重复的,并且缺乏一致性。
学习向量量化
和 K-means 的不同:
- 每个样例有类别标签,即 LVQ 是一种监督式学习;
- 输出不是每个簇的划分,而是每个类别的原型向量;
- 每个类别的原型向量不是简单的均值向量,考虑了附近非 / 同样例的影响。










高斯混合聚类
步骤
- 初始化 高斯混合成分的个数 k ,假设高斯混合分布模型参数 α(高斯混合系数)μ (均值) , Σ(协方差矩阵);
- 分别计算每个样本点的 后验概率 (该样本点属于每一个高斯模型的概率);
- 迭代 αμ , Σ;
- 重复第二步直到收敛。
难点
- 后验概率 (该样本点属于每一个高斯模型的概率)的计算:

- 上述公式由 7.18 相减化简而来

- 上述公式由 7.18 相减化简而来


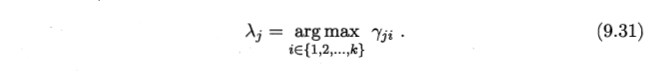
- 怎样迭代 αμ , Σ;
- α ——通过样本加权平均值来估计
- Σ ——通过样本加权平均值来估计
- μ ——由样本属于该成分的平均后验概率确定
- α ——通过样本加权平均值来估计
例子

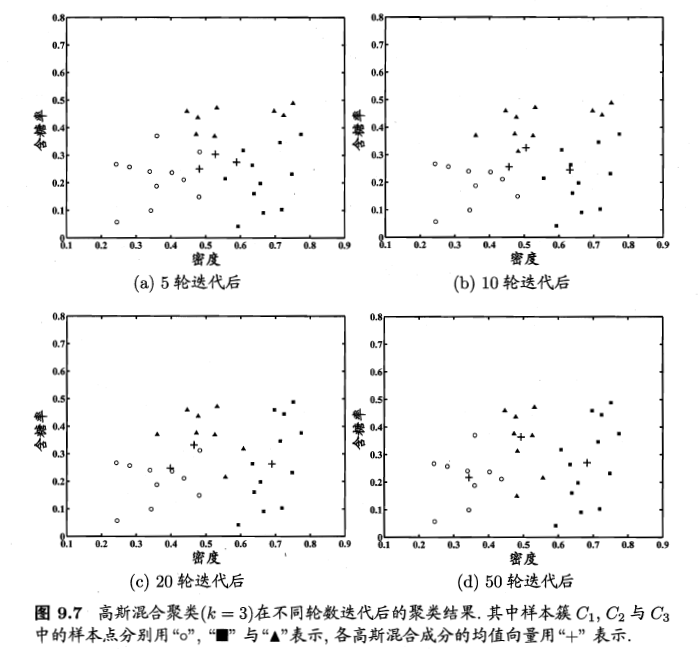
EM思想的体现

小结

9.5 密度聚类
密度聚类:根据样本分布的紧密程度确定。密度聚类算法从样本密度的角度考察样本之间的连接性,并基于可连接样本不断扩展聚类簇。

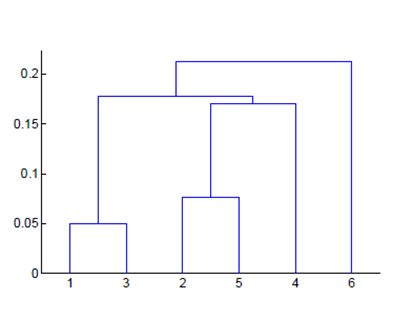
9.6 层次聚类
在不同层次对数据集进行划分,形成树形的聚类结构。
聚集策略:自底向上
分拆策略:自顶向下