
作者主页: 作者主页
本篇博客专栏:C++
创作时间 :2024年7月22日


什么是二叉搜索树?
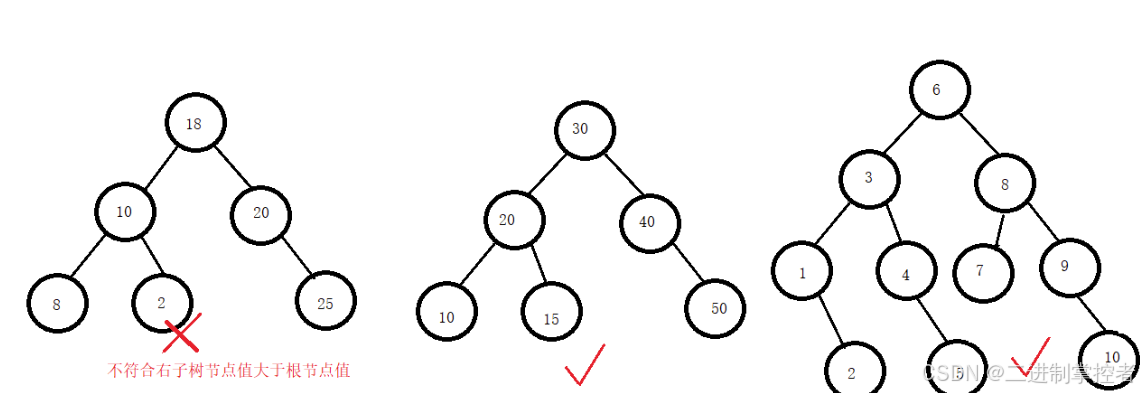
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
如何建立一颗二叉搜索树?
建立一颗二叉搜索树一般有下面几个步骤,首先我们要建立一颗空树,然后不断的去插入节点,前面我们说过对于一颗二叉搜索树,小于节点对应的值放在左边,大于节点对应的值放在右边。
想要插入一个节点,我们就要从根节点开始比较,如何小于就往右边走,大于就往左边走。
想要查找一个节点,我们也是从根节点开始,找到合适的位置之后插入。
二叉搜索树的实现
BST树的基本结构:
节点结构:
template<class K> struct BSTNode { K _key; BSTNode<K>* _left; BSTNode<K>* _right; BSTNode(const K& key) :_key(key) ,_left(nullptr) ,_right(nullptr) {} };这就是一个二叉搜索树对应的节点的基本结构,我们是基于链表来实现他的,包括对应的值,还有左子树,右子树。
查找对应的值是否存在:
查找对应的值我们还是那个思路,就是比对应的节点小就往左边走,大就往右边走。
bool Find(const K& key) { Node* cur = _root; while (cur) { if (cur->_key < key) { cur = cur->_right; } else if (cur->_key > key) { cur = cur->_left; } else if (cur->_key == key) { return true; } } return false; }插入一个值:
插入也是比较简单的,就是一直往下找,当下一个为空时,就直接插入。
这里还要注意如果已经存在这个值了,就会插入失败,还有最后还要判断一下是插入在左边还是右边。
bool Insert(const K& key) { if (_root == nullptr) { _root = new Node(key); return true; } Node* parent = nullptr; Node* cur = _root; while (cur) { if (cur->_key < key) { parent = cur; cur = cur->_right; } else if (cur->_key > key) { parent = cur; cur = cur->_left; } else return false; } cur = new Node(key); if (parent->_key < key) { parent->_right = cur; } else if (parent->_key > key) { parent->_left = cur; } return true; }中序遍历:
我们在看到中序遍历之后其实也能初步的明白搜索二叉树的一个作用,那就是排序,因为中序遍历的结果就是一个升序的结果。
中序遍历的结果我们也已经在前面的二叉树章节中讲清楚,这里我们不再多说。
void _Inorder(Node* root) { if (root == nullptr) { return; } _Inorder(root->_left); cout << root->_key << " "; _Inorder(root->_right); }删除:
最后我们来说一下删除,这个是最麻烦的一个,因为删除可以分为多种情况,比如如果要删除的这个节点没有孩子或者只有一个孩子,那么我们直接让这个节点的父亲指向另一个对应的节点。比如他是左孩子,那就指向右孩子,相反也是如此。
但如果是中间的某个节点怎么办,删除这个节点之后我们后面要如何去调整呢,这里我们就要找一个替代节点来代替要删除的这个节点,那我们该找谁呢?
我们其实可以选择这两个:左子树的最大节点,右子树的最小节点。仔细观察就可以发现,这两个节点都是符合逻辑的。这里我们找的是右子树的最小节点。
bool erase(K& key) { Node* cur = _root; Node* parent = nullptr; while (cur) { if (cur->_key < key) { parent = cur; cur = cur->_right; } else if (cur->_key > key) { parent = cur; cur = cur->_left; } else { //删除 //0 1个孩子 if (cur->_left == nullptr) { if (parent == nullptr)//如果一棵树只有两个节点,然后parent此时可能就是nullptr,那么就要进行这一步,直接让_root指向cur的不是空的那个节点 { _root = cur->_right; } else { if (parent->_left == cur) { parent->_left = cur->_right; } else parent->_right = cur->_right; } delete cur; return true; } else if (cur->_right == nullptr) { if (parent==nullptr) { parent = cur->_left; } else { if (parent->_left == cur) { parent->_left = cur->_left; } else parent->_right = cur->_left; } delete cur; return true; } //两个孩子 else { //找右子树最小节点 Node* rightMin = cur->_right; Node* rightMinP = cur;//防止未进入while循环,所以定义成cur while (rightMin->_left) { rightMinP = rightMin; rightMin = rightMin->_left; } cur->_key = rightMin->_key; //这里要看右边的情况 if (rightMinP->_left == rightMin)//如果右边的rightMin的左边还有节点 { rightMinP->_left = rightMin->_right; } else rightMinP->_right = rightMin->_right;//如果右边的rightMin的左边为空了 delete rightMin; return true; } } } }二叉搜索树的应用
1. K模型 :
K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到的值。
比如:给一个单词word,判断该单词是否拼写正确,具体方式如下:
以词库中所有单词集合中的每个单词作为key,构建一棵二叉搜索树
在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误。
2. KV模型 :
每一个关键码key,都有与之对应的值Value,即<Key, Value>的键值对。该种方
式在现实生活中非常常见:
比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文<word, chinese>就构成一种键值对;
再比如统计单词次数,统计成功后,给定单词就可快速找到其出现的次数,单词与其出 现次数就是<word, count>就构成一种键值对。
二叉搜索树的性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数,即结点越深,则比较次数越多。
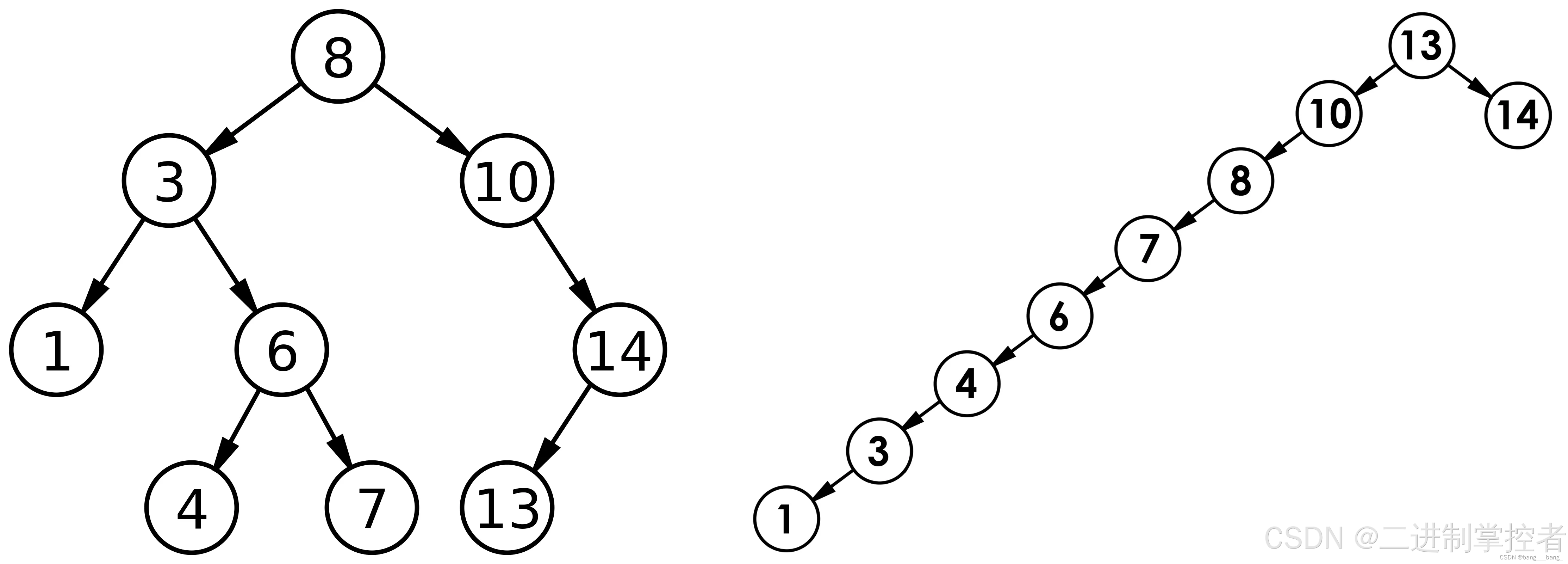
但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:
最优情况下:二叉搜索树为完全二叉树(或者接近完全二叉树),其平均比较次数为:log(N)
最差情况下:二叉搜索树退化为单支树(或者类似单支),其平均比较次数为 N
如果退化为单支树,二叉搜索树的性能就失去了。那能否进行改进?无论按照什么次序插入关键码,都能达到最优?这就需要AVL树和红黑树了。
最后:
十分感谢你可以耐着性子把它读完和我可以坚持写到这里,送几句话,对你,也对我:
1.一个冷知识:
屏蔽力是一个人最顶级的能力,任何消耗你的人和事,多看一眼都是你的不对。
2.你不用变得很外向,内向挺好的,但需要你发言的时候,一定要勇敢。
正所谓:君子可内敛不可懦弱,面不公可起而论之。
3.成年人的世界,只筛选,不教育。
4.自律不是6点起床,7点准时学习,而是不管别人怎么说怎么看,你也会坚持去做,绝不打乱自己的节奏,是一种自我的恒心。
5.你开始炫耀自己,往往都是灾难的开始,就像老子在《道德经》里写到:光而不耀,静水流深。
最后如果觉得我写的还不错,请不要忘记点赞✌,收藏✌,加关注✌哦(。・ω・。)
愿我们一起加油,奔向更美好的未来,愿我们从懵懵懂懂的一枚菜鸟逐渐成为大佬。加油,为自己点赞!
