机器学习西瓜书学习笔记【第五章】
第五章 神经网络
5.1神经元模型
神经网络的最基本的构成元素是神经元。生物神经网络中各个网络之间相互连接,通过神经递质相互传递信息。如果某个神经元接收了足够多的神经递质(乙酰胆碱),那么其点位变会积累地足够高,从而超过某个阈值。超过这个阈值之后,这个神经元变会被激活,达到兴奋的状态,而后发送神经递质给其他的神经元。
MP神经元模型
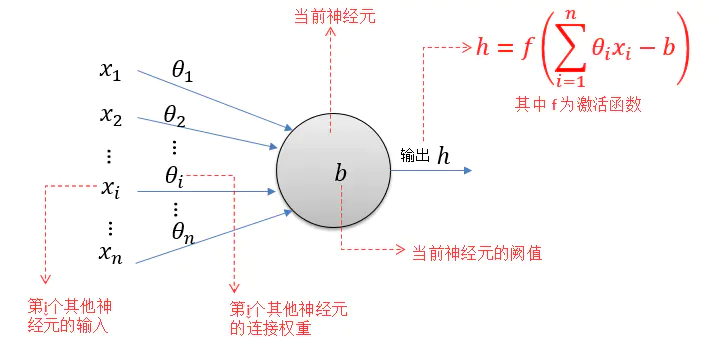
激活函数
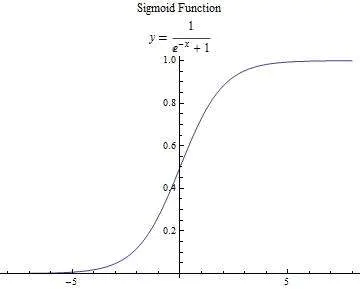
函数的值域是(0,1),即函数值落在0到1之间。S函数的性质有可以将较大范围内变化的输入值压缩到**(0,1)区间内,因此也被成为挤压函数**。
5.2 感知机与多层网络
学习
学习:从已知数据中学得模型(确定权重 ω i {\omega}_{i} ωi)
本质:不断更改权重( ω i {\omega}_{i} ωi),使得模型求出的预测值尽可能地接近真实值。
感知机
感知机:两层神经元组成。
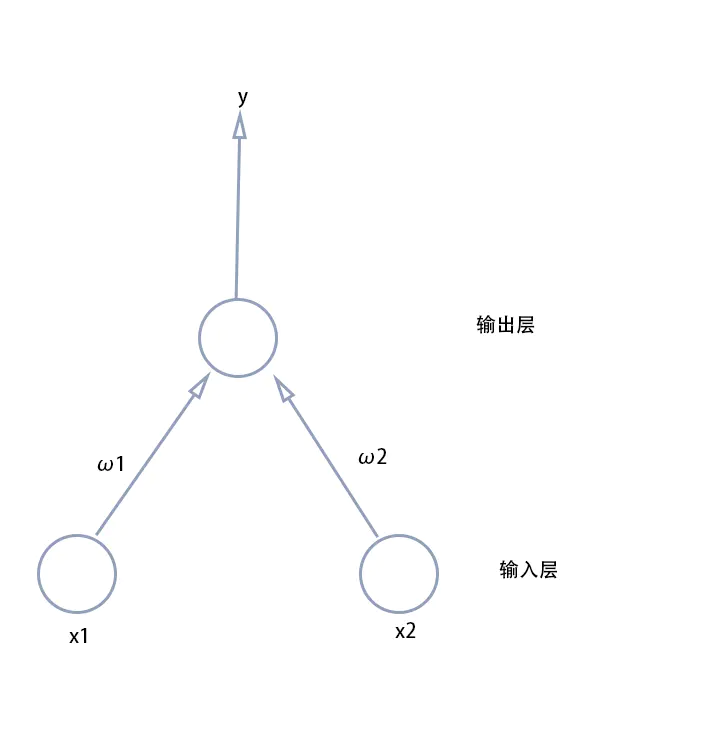
通过感知机实现逻辑运算,在MP神经元模型中,有输出:
y = f ( ∑ i ω i x i − θ ) y=f({\textstyle \sum_{i}^{}} {\omega }_{i}{x}_{i}-\theta ) y=f(∑iωixi−θ)
假设激活函数为阶跃函数 s g n ( x ) sgn(x) sgn(x):
KaTeX parse error: {equation} can be used only in display mode.\geKaTeX parse error: Expected 'EOF', got '}' at position 3: 0;}̲\\ 1& \text{x<0…
通过制定权重和阈值得到可以进行逻辑运算的感知机,那么如果给定训练数据集,同样我们可以通过学习得到相应地权重和阈值。
阈值b可以看做是一个输入固定为-1.0对应连接权重ωn+1的哑结点。通过这样定义阈值,则可以将学习权重和阈值简化为只学习权重。
感知机的学习规则很简单,对于训练样本(x,y),若感知机当前的输出为y’,则感知机的权重调整如下:
Δ ω i = η ( y − y ′ ) x i \Delta{\omega }_{i}=\eta (y-y'){x}_{i} Δωi=η(y−y′)xi
ω i ← ω i + Δ ω i {\omega }_{i}\gets{\omega }_{i}+\Delta{\omega }_{i} ωi←ωi+Δωi
其中, η {\eta} η为学习速率。若感知机对样本的预测正确的话,即** y ′ y' y′= y y y**,则感知机不发生任何变化。若其预测错误,则根据错误的程度进行相应权重的调整。
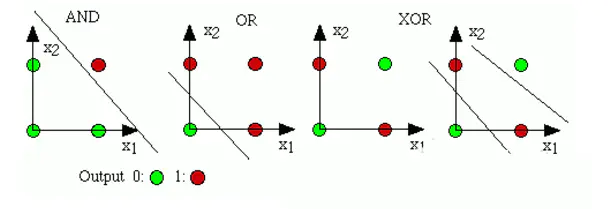
左面三个是通过线性分割实现,而最右侧的异或则无法通过线性分割实现。
学习率
学习率是每次迭代中成本函数最小化的量,梯度下降到成本函数最小值所对应的速率就是学习率。
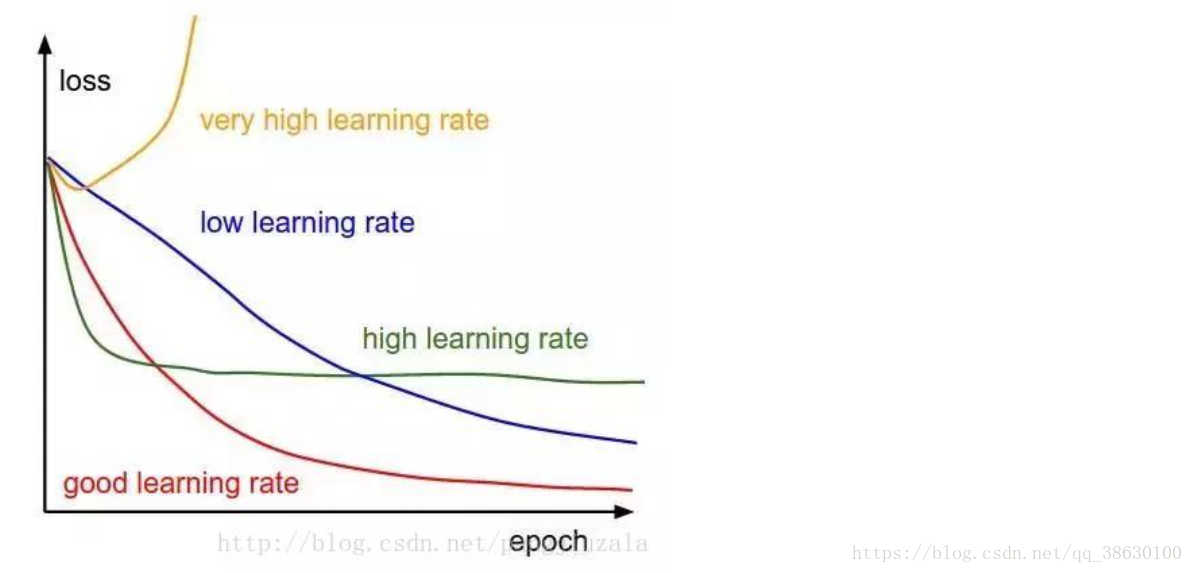
成本/损失函数
当建立一个神经网络的时候,神经网络会试图将输出预测尽可能地接近实际值。使用成本函数函数来衡量网络的准确性。成本函数会在发生错误的时候处罚网络。
目的是为了能够提高我们的预测精度,减少误差,从而最大限度的降低成本。最优化的输出即使成本/损失函数最小的输出。
梯度下降
梯度下降是最小化成本的优化算法,找到最小化的损失函数和模型参数值。
5.3 BP神经网络(误差逆传播)
①BP神经网络等于叠加多个感知机来实现非线性可分。(最少3层)
②梯度下降策略:以目标的负梯度方向对参数进行调整(此外还有牛顿法、最小二乘法等策略)
③第K个训练例的均方误差:
④更新权重
基本原理与感知机相同。
神经网络的思路总结:
搜集数据集( x i {x}_{i} xi,y),将 x i {x}_{i} xi代入初始的神经网络模型,计算估计值 y ^ \hat{y} y^
根据 y ^ \hat{y} y^与y的差异不断更改权重 ω i {\omega}_{i} ωi,使其误差尽可能的小(梯度下降)
大量数据训练后,再输入新的数据x,模型就可以求出y用于分类/预测/评价了
5.4 全局最小与局部极小
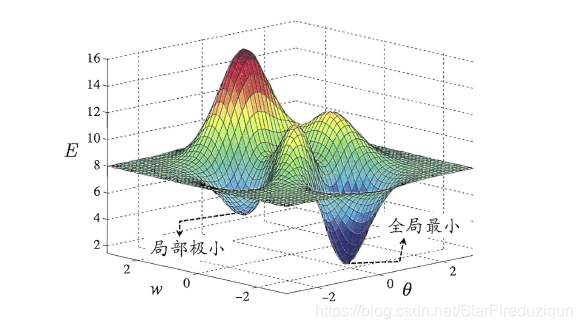
局部最小值是在某一区域内,函数的取值达到了最小,但是如果将这个区域扩展到定义域上来,那么这个局部最小值就不一定是最小的。
全局最小值,是在定义域内,函数值最小。全局最小一定是局部最小值,但“局部极小 ” 不一定是“全局最小 ”。因此我们的目标是找到 “ 全局最小 ”。
可能存在多个局部极小值,但却只会有一个全局最小值。
5.5 其他常见神经网络
RBF网络
- BP 网络
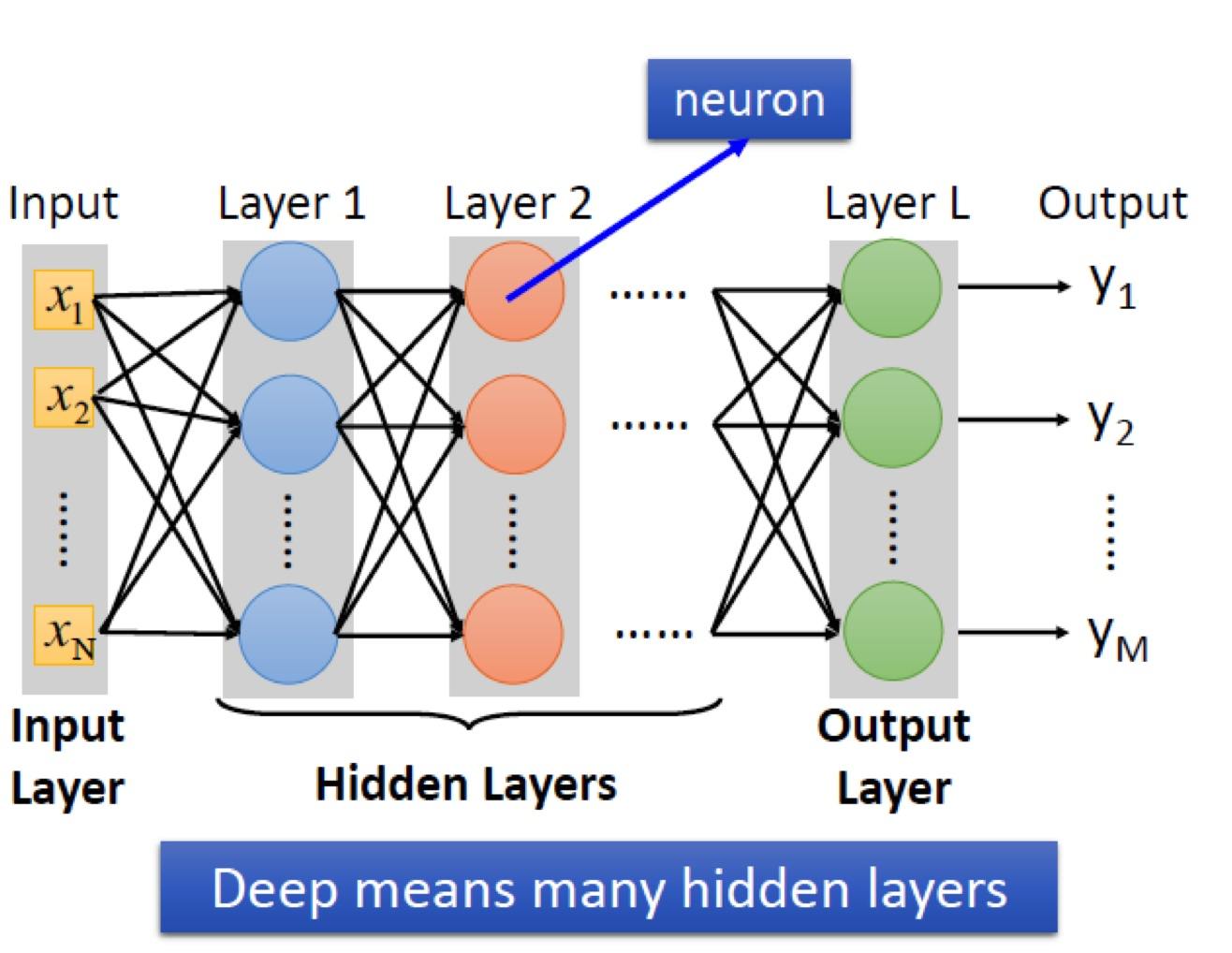
- RBF 网络:
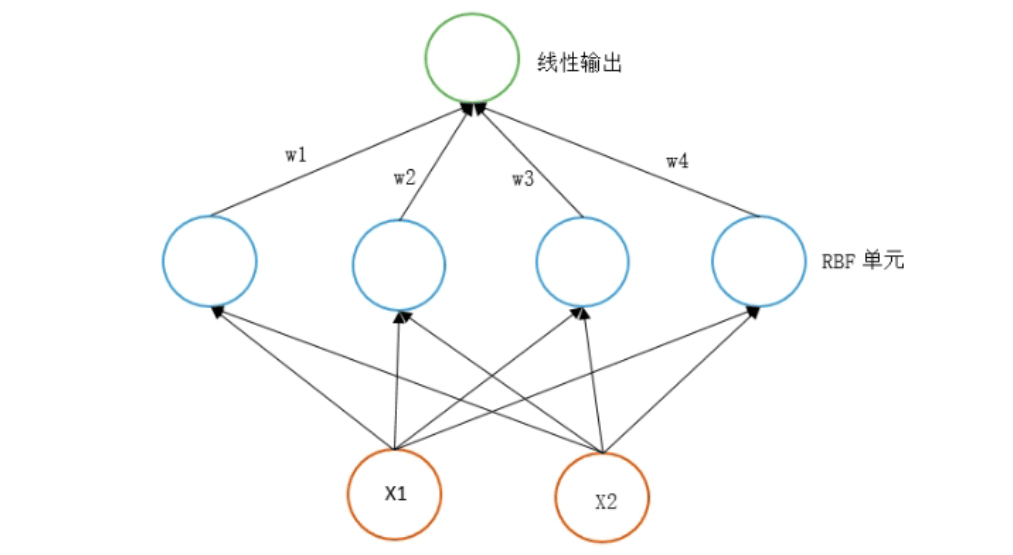
- **径向基函数:**是一个取值仅依赖于到原点距离的实值函数。此外,也可以按到某一中心点c的距离来定义。
- **RBF 网络结构:**RBF Network 通常只有三层。输入层、中间层计算输入 x 矢量与样本矢量 c 欧式距离的值,输出层算它们的线性组合。
- 训练 RBF 网络步骤:
- 第一步,确定神经元中心,常用的方法包括随机采样、聚类。
- 第二步,利用 BP 算法来确定参数。
RBF 与 BP 最重要的区别
1 中间层神经元的区别。
- RBF: 神经元是一个以gaussian函数为核函数的神经元。
2 中间层数的区别。
- 中间层只有一层。经过训练后每一个神经元得以确定输入权重:即每一个神经元知道要在什么样的输入值下引起最大的响应。
3 运行速度的区别。
- 原因是因为层数,层数越少,需要确定的权重(weight)越少,越快。
- 为什么三层可以做这么多层的事儿?原因是核函数的输出: 是一个局部的激活函数。在中心点那一点有最大的反应;越接近中心点则反应最大,远离反应成指数递减。
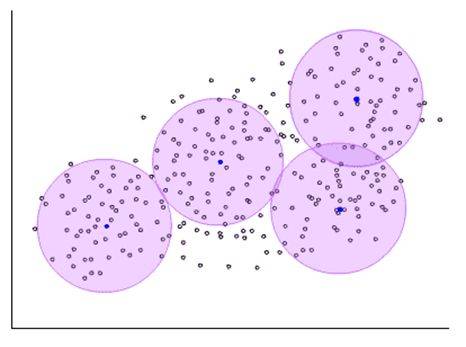
ART网络
**竞争型学习:**是神经网络中一种常用的无监督学习策略,在使用该策略时,网络的输出神经元相互竞争,每一时刻仅有一个竞争获胜的神经元被激活,其他神经元的状态被抑制,这种机制也称 “胜者通吃” 原则。ART 就是竞争型学习的重要代表。
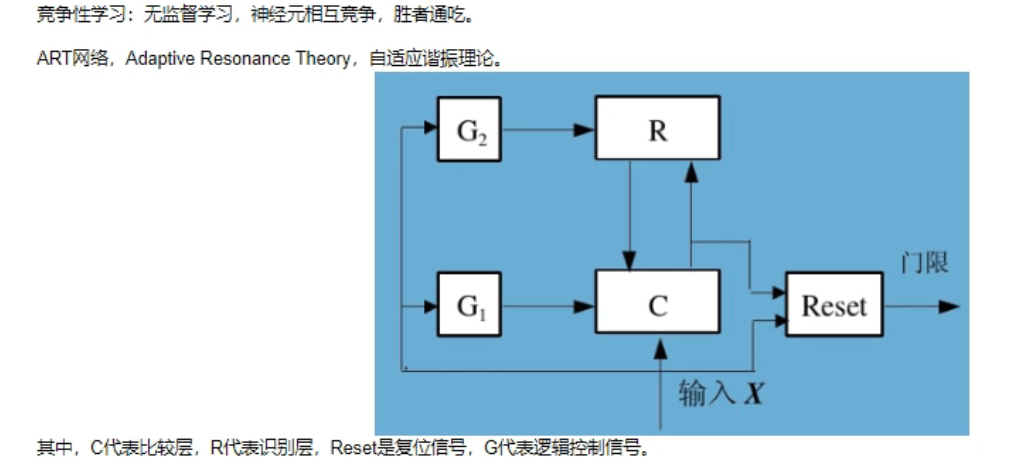
ART 网络:
该网络由比较层、识别层、识别阈值和重置模块构成。
- 比较层:负责接收输入样本,并将其传递给识别层神经元。
- 识别层:识别层每个神经元对应一个模式类,神经元数目可在训练过程中动态增长以增加新的模式类。
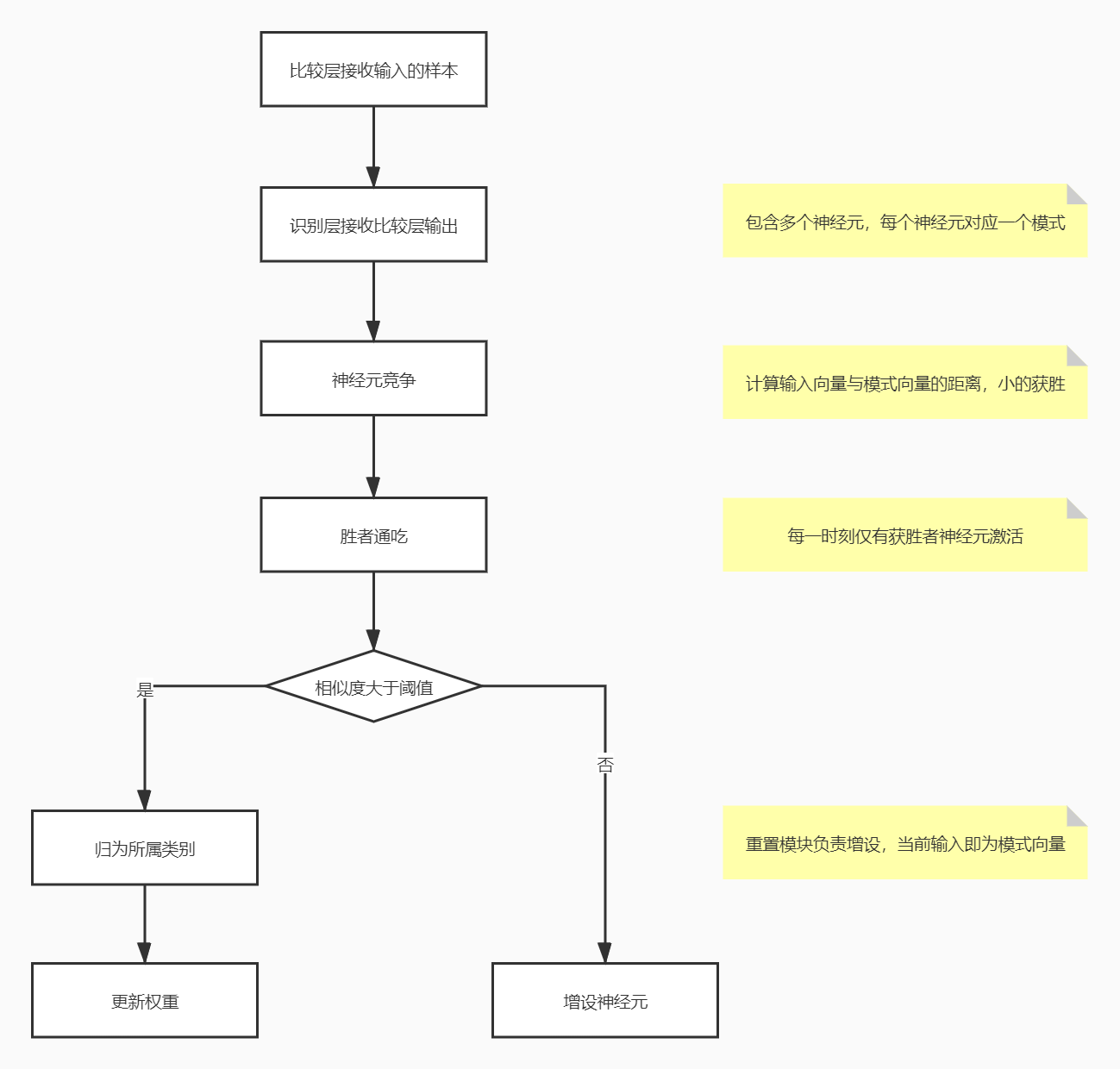
- **阈值:**显然,识别阈值对 ART 网络的性能有重要影响,当识别阈值较高时,输入样本会被分成较多、较精细的模式类,而如果识别阈值较低,则会产生比较少、比较粗略的模式类。
- **ART 优点:**可进行增量学习或在线学习。
SOM网络
级联相关网络
Elman网络
Boltzmann机
