文章目录
- 希尔密码
- Z 256 下的希尔密码 Z_{256}下的希尔密码 Z256下的希尔密码
- 移位密码
- 希尔密码( Z 256 Z_{256} Z256)
- 迭代密码
- 参考文献
希尔密码
矩阵
矩阵基本概念
在数学中,矩阵(Matrix)是一个按照长方阵列排列的复数或实数集合,最早来自于方程组的系数及常数所构成的方阵。这一概念由19世纪英国数学家凯利首先提出。
由 m × n 个数 a i j a_{ij} aij排成的m行n列的数表称为m行n列的矩阵,简称m × n矩阵。
A = [ A 11 A 12 . . . A 1 n A 21 A 22 . . . A 2 n . . . . . . . . . . . . A m 1 A m 2 . . . A m n ] A=\begin{bmatrix} A_{11} & A_{12}&...&A_{1n} \\A_{21} & A_{22}&...&A_{2n} \\...& ...& ...& ... \\ A_{m1} & A_{m2}&...&A_{mn} \end{bmatrix} A=A11A21...Am1A12A22...Am2............A1nA2n...Amnm×n 个数称为矩阵A的元素,简称为元。
数 a i j a_{ij} aij位于矩阵A的第i行第j列,称为矩阵A的 ( i , j ) (i,j) (i,j)元
m×n矩阵A也记作 A m n A_{mn} Amn。
元素是实数的矩阵称为实矩阵,元素是复数的矩阵称为复矩阵。
行数与列数都等于n的矩阵称为n阶矩阵或n阶方阵。
特征值与特征向量:
n×n的方块矩阵A的一个特征值和对应特征向量是满足 A v = λ v Av=\lambda v Av=λv的标量以及非零向量。其中 v v v为特征向量, λ \lambda λ为特征值。
线性变换的特征向量是指在变换下方向不变,或者简单地乘以一个缩放因子的非零向量。
特征向量对应的特征值是它所乘的那个缩放因子。
行列式基本概念
一个n×n的正方矩阵A的行列式记为 d e t ( A ) det(A) det(A)或 ∣ A ∣ |A| ∣A∣,行列式的值仅仅是一个数,不是矩阵之类的。
2×2矩阵的行列式计算方式如下:
d e t ( a b c d ) = a d − c b det\begin{pmatrix} a & b \\ c & d \end{pmatrix}=ad-cb det(acbd)=ad−cb元素 a i j a_{ij} aij的代数余子式
(1)在n阶行列式中,把元素 a i j a_{ij} aij所在的第i行和第j列划去后,留下来的n-1阶行列式叫做元素 a i j a_{ij} aij的余子式,记作 M i j M_{ij} Mij。
(2)将余子式 M i j M_{ij} Mij再乘以-1的i+j次幂记为 A i j 。 A_{ij}。 Aij。即: A i j = ( − 1 ) i + j M i j A_{ij}=(-1)^{i+j}M_{ij} Aij=(−1)i+jMij
(3) A i j A_{ij} Aij叫做元素 a i j a_{ij} aij的代数余子式。
(4)一个元素 a i j a_{ij} aij的代数余子式与该元素本身没什么关系,只与该元素的位置有关。计算行列式值
n×n矩阵的行列式计算方式如下:
其任意行(或列)的元素与对应的代数余子式乘积之和
A = [ A 11 A 12 . . . A 1 n A 21 A 22 . . . A 2 n . . . . . . . . . . . . A n 1 A n 2 . . . A n n ] d e t ( A ) = ∣ A ∣ = a i 1 A i 1 + . . . + a i n A i n = ∑ j = 1 n a i j d e t ( A i j ) 即:行列式等于它的任一行 ( 列 ) 的所有元素与其对应的代数余子式的乘积之和 A=\begin{bmatrix} A_{11} & A_{12}&...&A_{1n} \\A_{21} & A_{22}&...&A_{2n} \\...& ...& ...& ... \\ A_{n1} & A_{n2}&...&A_{nn} \end{bmatrix} \\ \\det(A)=|A|=a_{i1}A_{i1}+...+a_{in}A_{in}=\sum_ {j=1}^{n}a_{ij}det(A_{ij}) \\即:行列式等于它的任一行(列)的所有元素与其对应的代数余子式的乘积之和 A=A11A21...An1A12A22...An2............A1nA2n...Anndet(A)=∣A∣=ai1Ai1+...+ainAin=j=1∑naijdet(Aij)即:行列式等于它的任一行(列)的所有元素与其对应的代数余子式的乘积之和两个性质
d e t ( I m ) = 1 d e t ( A B ) = d e t ( A ) d e t ( B ) det(I_m)=1 \\det(AB)=det(A)det(B) det(Im)=1det(AB)=det(A)det(B)
特殊矩阵关于乘法运算构成群
1、 A l m A_{lm} Alm B m n = C l n B_{mn}=C_{ln} Bmn=Cln
c i , k = ∑ j = 1 m a i , j b j , k , 1 ≤ i ≤ l , 1 ≤ k ≤ n c_{i,k}=\sum_{j=1}^ma_{i,j}b_{j,k},1 \le i \le l,1 \le k \le n ci,k=∑j=1mai,jbj,k,1≤i≤l,1≤k≤n
2、 ( A B ) C = A ( B C ) (AB)C=A(BC) (AB)C=A(BC)
3、一般矩阵不满足交换律 A B ≠ B A AB\not = BA AB=BA。
4、矩阵有单位矩阵(对角线为1,其余为0) I m = [ 1 0 . . . 0 0 1 . . . 0 . . . . . . . . . . . . 0 0 . . . 1 ] I_m=\begin{bmatrix} 1&0&...&0 \\0 & 1&...&0 \\...& ...& ...& ... \\ 0& 0&...&1 \end{bmatrix} Im=10...001...0............00...1
其中,22矩阵 I 2 = [ 1 0 0 1 ] I_2=\begin{bmatrix} 1&0 \\ 0&1 \end{bmatrix} I2=[1001]
A I m = A , I m B = B AI_m=A,I_mB=B AIm=A,ImB=B
5、如果A和B可逆
A m m A m m − 1 = A m m − 1 A m m = I m A_{mm}A_{mm}^{-1}=A_{mm}^{-1}A_{mm}=I_m AmmAmm−1=Amm−1Amm=Im
注意:可逆矩阵关于乘法运算不一定符合交换律,不一定构成交换群。
A怎么才能可逆呢? d e t ( A ) ≠ 0 det(A)\not =0 det(A)=0则A可逆。
G L n ( R ) = { A ∈ M n ( R ) ∣ d e t ( A ) ≠ 0 } GL_n(R)=\{A \in M_n(R)|det(A)\not =0\} GLn(R)={A∈Mn(R)∣det(A)=0},即所有n阶可逆实矩阵 G L n ( R ) GL_n(R) GLn(R)关于矩阵乘法构成群。
6、伴随矩阵 A ∗ A^* A∗
A各元素代数余子式 A j i A_{ji} Aji组成伴随矩阵 A ∗ = ( A i j ) A^*=(A_{ij}) A∗=(Aij)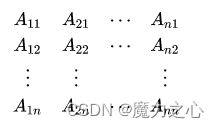
特别注意:i和j的顺序不一样,代数余子式 A j i A_{ji} Aji在伴随矩阵中按列排列。
伴随矩阵 A ∗ A^* A∗的一些基本性质
(1)A可逆当且仅当 A ∗ A^* A∗可逆。
(2)如果A可逆, A ∗ = ∣ A ∣ A − 1 A^*=|A|A^{-1} A∗=∣A∣A−1
= > ∣ A ∣ − 1 A ∗ = A − 1 =>|A|^{-1}A^*=A^{-1} =>∣A∣−1A∗=A−1R的逆元
在R(实数)乘法群中
1 为单位元。 设 a ∈ R , a ∗ 1 a = 1 = > 则 a 逆元 a − 1 为 1 a 1为单位元。 \\设a \in R ,a*\frac 1 a=1\\=>则a逆元a^{-1}为\frac 1 a 1为单位元。设a∈R,a∗a1=1=>则a逆元a−1为a1
因此, ∣ A ∣ − 1 = 1 ∣ A ∣ = > A − 1 = A ∗ 1 ∣ A ∣ |A|^{-1}=\frac 1 {|A|}\\=>A^{-1}=A^* \frac 1 {|A|} ∣A∣−1=∣A∣1=>A−1=A∗∣A∣1二阶方阵可用下面方法求逆:
A i j 为 d e t ( A ) ( 也可写成 ∣ A ∣ ) 中,元素 a i j 的代数余子式。 当矩阵的阶数等于一阶时,伴随矩阵为一阶单位方阵。 二阶矩阵的伴随矩阵 A ∗ 求法口诀:主对角线元素互换,副对角线元素变号 伴随矩阵 A ∗ = [ a 22 − a 12 − a 21 a 11 ] A − 1 = 1 ∣ A ∣ A ∗ A_{ij}为det(A)(也可写成|A|)中,元素a_{ij}的代数余子式。 \\当矩阵的阶数等于一阶时,伴随矩阵为一阶单位方阵。 \\二阶矩阵的伴随矩阵A^*求法口诀:主对角线元素互换,副对角线元素变号 \\伴随矩阵A^*=\begin{bmatrix} a_{22}&- a_{12} \\-a_{21}& a_{11} \end{bmatrix} \\A^{-1}=\frac 1 {|A|}A^* Aij为det(A)(也可写成∣A∣)中,元素aij的代数余子式。当矩阵的阶数等于一阶时,伴随矩阵为一阶单位方阵。二阶矩阵的伴随矩阵A∗求法口诀:主对角线元素互换,副对角线元素变号伴随矩阵A∗=[a22−a21−a12a11]A−1=∣A∣1A∗高阶矩阵可以用矩阵的初等行变换。
在线性代数中,矩阵的初等行变换是指以下三种变换类型 :
( 1 ) 交换矩阵的两行(对调 i , j ,两行记为 r i , r j ); ( 2 ) 以一个非零数 k 乘矩阵的某一行所有元素(第 i 行乘以 k 记为 r i × k ); ( 3 ) 把矩阵的某一行所有元素乘以一个数 k 后加到另一行对应的元素 ( 第 j 行乘以 k 加到第 i 行记为 r i + k ∗ r j ) 。 (1) 交换矩阵的两行(对调i,j,两行记为r_i,r_j); \\(2) 以一个非零数k乘矩阵的某一行所有元素(第i行乘以k记为r_i×k); \\(3) 把矩阵的某一行所有元素乘以一个数k后加到另一行对应的元素(第j行乘以k加到第i行记为r_i+k*r_j)。 (1)交换矩阵的两行(对调i,j,两行记为ri,rj);(2)以一个非零数k乘矩阵的某一行所有元素(第i行乘以k记为ri×k);(3)把矩阵的某一行所有元素乘以一个数k后加到另一行对应的元素(第j行乘以k加到第i行记为ri+k∗rj)。
加解密原理
密钥
- 设m为正整数,P和C分别是原文和密文。
P = C = ( Z 26 ) m P=C=(Z_{26})^m P=C=(Z26)m
这里的m为m维向量空间,m维欧氏空间的意思
26即26个英文字母,也可以为 ( Z 256 ) m (Z_{256})^m (Z256)m(一个字节256个数字) - 设m为2,即:每次对2个数字(即:2个英文字母或2个字节)进行加解密。
明文: x = ( x 1 , x 2 ) x=(x_1,x_2) x=(x1,x2),密文 y = ( y 1 , y 2 ) y=(y_1,y_2) y=(y1,y2)
密钥 : K = [ K 11 K 12 K 21 K 22 ] 密钥:K=\begin{bmatrix} K_{11}& K_{12} \\ K_{21}& K_{22} \end{bmatrix} 密钥:K=[K11K21K12K22]
特别注意:在 Z 26 Z_{26} Z26或 Z 256 Z_{256} Z256下进行运算。
加密函数
y 1 = ( x 1 , x 2 ) [ k 11 k 12 k 21 k 22 ] m o d 26 ( 或 256 ) y_1=(x_1,x_2) \begin{bmatrix} k_{11}& k_{12} \\ k_{21}& k_{22} \end{bmatrix}\quad mod\quad 26(或256) y1=(x1,x2)[k11k21k12k22]mod26(或256)
特别注意上面函数是在 Z 26 或 Z 256 下进行 Z_{26}或Z_{256}下进行 Z26或Z256下进行
即:
y 1 = ( k 11 x 1 + k 21 x 2 ) m o d 26 ( 或 256 ) y 2 = ( k 21 x 1 + k 22 x 2 ) m o d 26 ( 或 256 ) y_1=(k_{11}x_1+k_{21}x_2)\quad mod \quad 26(或256) \\y_2=(k_{21}x_1+k_{22}x_2) \quad mod \quad 26(或256) y1=(k11x1+k21x2)mod26(或256)y2=(k21x1+k22x2)mod26(或256)
解密函数
y = x K = > y K − 1 = ( x K ) K − 1 = x ( K K − 1 ) = x I m = x y=xK\\=>yK^{-1}=(xK)K^{-1}=x(KK^{-1})=xI_m=x y=xK=>yK−1=(xK)K−1=x(KK−1)=xIm=x
= > x = y K − 1 =>x=yK^{-1} =>x=yK−1
特别注意上面函数是在 Z 26 或 Z 256 下进行 Z_{26}或Z_{256}下进行 Z26或Z256下进行
Z 26 上的运算( Z 256 与此类似) Z_{26}上的运算(Z_{256}与此类似) Z26上的运算(Z256与此类似)
∣ K ∣ − 1 = ? |K|^{-1}=? ∣K∣−1=?
这是错的: K − 1 = 1 ∣ K ∣ K ∗ ,这不是在 R 乘法群,是在 Z 26 乘法群。 K − 1 = ∣ K ∣ − 1 K ∗ ∣ K ∣ − 1 = ? 这是错的:K^{-1}=\frac 1 {|K|}K^*,这不是在R乘法群,是在Z_{26}乘法群。 \\K^{-1}=|K|^{-1}K^* \\|K|^{-1}=? 这是错的:K−1=∣K∣1K∗,这不是在R乘法群,是在Z26乘法群。K−1=∣K∣−1K∗∣K∣−1=?∣ K ∣ = ? |K| =? ∣K∣=?
∣ K ∣ = ∑ j = 1 n a i j ( − 1 ) i + j d e t ( A i j ) ,这也是错误的!! 这才是对的: ∣ K ∣ = ∑ j = 1 n a i j ( − 1 ) i + j d e t ( A i j ) m o d 26 思考一下为什么? \\|K| =\sum_ {j=1}^{n}a_{ij}(-1)^{i+j}det(A_{ij}) ,这也是错误的!! \\这才是对的:|K| =\sum_ {j=1}^{n}a_{ij}(-1)^{i+j}det(A_{ij}) \quad mod \quad 26 \\ 思考一下为什么? ∣K∣=j=1∑naij(−1)i+jdet(Aij),这也是错误的!!这才是对的:∣K∣=j=1∑naij(−1)i+jdet(Aij)mod26思考一下为什么?K ∗ = ? K^*=? K∗=?
K i j = ( − 1 ) i + j M i j K_{ij}=(-1)^{i+j}M_{ij} Kij=(−1)i+jMij这也错了!?
是的,错了!这只是在R乘法群的运算!∣ K ∣ ≠ 0 = > K 可逆 |K|\not = 0=>K可逆 ∣K∣=0=>K可逆
这也是错误的,在 Z 26 Z_{26} Z26中要变换如下:
g c d ( ∣ K ∣ , 26 ) = 1 = > K 在 Z 26 可逆 gcd(|K|,26)=1=>K在Z_{26}可逆 gcd(∣K∣,26)=1=>K在Z26可逆
例1
1 、取 K = [ K 11 K 12 K 21 K 22 ] = [ 19 17 2 9 ] ∣ K ∣ = ( 19 ∗ 9 − 17 ∗ 2 ) m o d 26 = 137 m o d 26 = 7 = > g c d ( 7 , 26 ) = 1 = > K 在 Z 26 中可逆。 2 、 7 ∗ 15 ≡ 1 ( m o d 26 ) = > 7 − 1 = 15 = > ∣ K ∣ − 1 = 15 3 、 K − 1 = ∣ K ∣ − 1 A ∗ = ∣ K ∣ − 1 [ K 11 − K 12 − K 21 K 22 ] = 15 [ 9 − 17 − 2 19 ] = 15 [ 9 9 24 19 ] K − 1 = [ 135 135 360 285 ] = [ 5 5 22 25 ] 4 、设原文 x = ( 18 , 7 ) ( 1 ) 密文 y = e k ( x ) = x K = ( 18 , 7 ) [ 19 17 2 9 ] = [ 356 , 359 ] = [ 18 , 5 ] ( 2 ) 原文 x = d k ( y ) = y K − 1 = [ 18 , 5 ] [ 5 5 22 25 ] = [ 200 , 215 ] = [ 18 , 7 ] = x 1、取K=\begin{bmatrix} K_{11}& K_{12} \\K_{21}& K_{22} \end{bmatrix}=\begin{bmatrix} 19 & 17 \\ 2&9 \end{bmatrix} \\|K|=(19*9-17*2) \quad mod \quad 26 \\=137 \quad mod \quad 26 =7 \\=>gcd(7,26)=1 \\=>K在Z_{26}中可逆。 \\2、7*15\equiv 1(mod \quad 26)=>7^{-1}=15=>|K|^{-1}=15 \\3、K^{-1}=|K|^{-1}A^*=|K|^{-1}\begin{bmatrix} K_{11}&- K_{12} \\-K_{21}& K_{22} \end{bmatrix} =15\begin{bmatrix} 9& -17 \\-2& 19 \end{bmatrix} \\ =15\begin{bmatrix} 9& 9 \\24& 19 \end{bmatrix} \\ K^{-1}=\begin{bmatrix} 135& 135 \\360& 285 \end{bmatrix} =\begin{bmatrix} 5& 5 \\22& 25 \end{bmatrix} \\ 4、设原文x=(18,7) \\ (1)密文y=e_k(x)=xK=(18,7)\begin{bmatrix} 19 & 17 \\ 2&9 \end{bmatrix} \\=[356,359]=[18,5] \\(2)原文x=d_k(y)=yK^{-1}=[18,5]\begin{bmatrix} 5& 5 \\22& 25 \end{bmatrix} \\=[200,215] =[18, 7]=x 1、取K=[K11K21K12K22]=[192179]∣K∣=(19∗9−17∗2)mod26=137mod26=7=>gcd(7,26)=1=>K在Z26中可逆。2、7∗15≡1(mod26)=>7−1=15=>∣K∣−1=153、K−1=∣K∣−1A∗=∣K∣−1[K11−K21−K12K22]=15[9−2−1719]=15[924919]K−1=[135360135285]=[522525]4、设原文x=(18,7)(1)密文y=ek(x)=xK=(18,7)[192179]=[356,359]=[18,5](2)原文x=dk(y)=yK−1=[18,5][522525]=[200,215]=[18,7]=x
关于负数取余问题:
1、当被除数能被除数整除时,无论被除数和除数的正负,余数都是0。
2、对于负数除以正数或,编译器会先将分子(即被除数的绝对值)转换为正整数进行取余运算。
Z 256 下的希尔密码 Z_{256}下的希尔密码 Z256下的希尔密码
概述
m ≥ 2 为正整数,表示 m 维向量空间 P 和 C 分别是原文和密文 P = C = ( Z 256 ) m K = { 定义在 Z 256 上的 m × m 的可逆矩阵 } 加解密 : z 256 上的加密: e K ( x ) = x K z 256 上的解密: d K ( y ) = y K − 1 m\ge 2为正整数,表示m维向量空间 \\P和C分别是原文和密文 \\P=C=(Z_{256})^m \\K=\{定义在Z_{256}上的m \times m的可逆矩阵\} \\加解密: \\z_{256}上的 加密:e_K(x)=xK \\z_{256}上的解密:d_K(y)=yK^{-1} m≥2为正整数,表示m维向量空间P和C分别是原文和密文P=C=(Z256)mK={定义在Z256上的m×m的可逆矩阵}加解密:z256上的加密:eK(x)=xKz256上的解密:dK(y)=yK−1
example
K密钥选择
- K的形式
取m=3,需要选择一个K(密钥)满足 k 在 Z 256 下可逆。即: g c d ( ∣ K ∣ , 26 ) = 1 k在Z_{256}下可逆。即:gcd(∣K∣,26)=1 k在Z256下可逆。即:gcd(∣K∣,26)=1。
具体原理见密码学原理精解【3】
K的形式如下面矩阵所示:
K = [ K 11 K 12 K 13 K 21 K 22 K 23 K 31 K 32 K 33 ] K=\begin{bmatrix} K_{11} & K_{12}&K_{13} \\K_{21} & K_{22}&K_{23} \\K_{31} & K_{32}&K_{33} \end{bmatrix} K=K11K21K31K12K22K32K13K23K33 - 计算K
使用Julia完成计算(也可使用C++完成)
1、定义K
julia> k=rand(0:255,3,3) 3×3 Matrix{Int64}: 180 191 64 128 120 63 139 27 168 2、选择K,计算det(k)。
using LinearAlgebra k=rand(0:255,3,3) dk=det(k) while abs(dk)<1.0 || abs(dk-trunc(Int,dk))>0.0 global k global dk k=rand(0:255,3,3) dk=det(k) sleep(1) println("try again") end dk=dk % 256 if dk<0 dk=256+dk end println(k) println(dk) julia> include("e:/learn/learn1.jl") try again try again [55 174 63; 47 135 200; 231 179 148] 200.0 3.保证K可逆。
using LinearAlgebra isOk=false k=rand(0:255,3,3) dk=det(k) println("trying") while gcd(trunc(Int,dk),256)!=1 || abs(dk)<1.0 ||abs(trunc(Int,dk)-dk)>0.000001 global k global dk k=rand(0:255,3,3) dk=det(k) dk=dk % 256 if dk<0 dk=256+dk end print(".") sleep(1) end println("I found out!") println(k) println(dk) julia> include("e:/learn/learn1.jl") trying ...I found out! [16 91 215; 171 253 50; 8 186 121] 121.0 julia> include("e:/learn/learn1.jl") trying ........I found out! [109 138 25; 62 128 229; 19 253 224] 207.0 在此,我们取K=
K = [ 16 91 215 171 253 50 8 186 121 ] K=\begin{bmatrix} 16 & 91 &215 \\171 & 253 &50 \\8 & 186&121 \end{bmatrix} K=1617189125318621550121
∣ K ∣ − 1 |K|^{-1} ∣K∣−1
∣ k ∣ = d e t ∣ k ∣ ∣ k ∣ − 1 = 12 1 − 1 = 201 |k|=det|k| \\|k|^{-1}=121^{-1}=201 ∣k∣=det∣k∣∣k∣−1=121−1=201
julia> for i in range(1,256) if (121*i) % 256==1 println(i) println(121*i) break end end 201 24321 K ∗ K^* K∗
- 下面是在 Z 26 Z_{26} Z26下的运算。
using LinearAlgebra k=[10 5 12 ;3 14 21;8 9 11] adjoint_k=[0 0 0;0 0 0;0 0 0] for i in range(1,3) index_i=[1,2,3] deleteat!(index_i,i) for j in range(1,3) global k index_j=[1,2,3] deleteat!(index_j,j) print([index_i,index_j],"=") println(k[index_i,index_j]) a_ij=(-1)^(i+j)*round(Int,det(k[index_i,index_j])) a_ij=a_ij % 26 if a_ij <0 a_ij=26+a_ij end adjoint_k[j,i]=a_ij end end println(adjoint_k) julia> include("e:/learn/learn1.jl") [[2, 3], [2, 3]]=[14 21; 9 11] [[2, 3], [1, 3]]=[3 21; 8 11] [[2, 3], [1, 2]]=[3 14; 8 9] [[1, 3], [2, 3]]=[5 12; 9 11] [[1, 3], [1, 3]]=[10 12; 8 11] [[1, 3], [1, 2]]=[10 5; 8 9] [[1, 2], [2, 3]]=[5 12; 14 21] [[1, 2], [1, 3]]=[10 12; 3 21] [[1, 2], [1, 2]]=[10 5; 3 14] [17 1 15; 5 14 8; 19 2 21] - Z 256 Z_{256} Z256下的运算
我们本次要用到的是模256,所以上面程序改下
using LinearAlgebra k=[16 91 215; 171 253 50; 8 186 121] adjoint_k=[0 0 0;0 0 0;0 0 0] for i in range(1,3) index_i=[1,2,3] deleteat!(index_i,i) for j in range(1,3) global k index_j=[1,2,3] deleteat!(index_j,j) print([index_i,index_j],"=") println(k[index_i,index_j]) a_ij=(-1)^(i+j)*round(Int,det(k[index_i,index_j])) a_ij=a_ij % 256 if a_ij <0 a_ij=256+a_ij end adjoint_k[j,i]=a_ij end end println(adjoint_k) julia> include("e:/learn/learn1.jl") [[2, 3], [2, 3]]=[253 50; 186 121] [[2, 3], [1, 3]]=[171 50; 8 121] [[2, 3], [1, 2]]=[171 253; 8 186] [[1, 3], [2, 3]]=[91 215; 186 121] [[1, 3], [1, 3]]=[16 215; 8 121] [[1, 3], [1, 2]]=[16 91; 8 186] [[1, 2], [2, 3]]=[91 215; 253 50] [[1, 2], [1, 3]]=[16 215; 171 50] [[1, 2], [1, 2]]=[16 91; 171 253] [65 51 75; 189 216 125; 86 56 7] K − 1 K^{-1} K−1
K − 1 = ∣ K ∣ − 1 K ∗ = 201 ∗ K ∗ = ? K^{-1}=|K|^{-1}K^*=201*K^*=? K−1=∣K∣−1K∗=201∗K∗=?
K*=[65 51 75; 189 216 125; 86 56 7] using LinearAlgebra adjoint_k=[65 51 75; 189 216 125; 86 56 7] k=201*adjoint_k for i in range(1,3) for j in range(1,3) a_ij=k[i,j] % 256 if a_ij <0 a_ij=256+a_ij end adjoint_k[j,i]=a_ij end end println(adjoint_k) julia> include("e:/learn/learn1.jl") [9 11 227; 101 152 37; 134 248 127] 现在K和K的逆都已经计算完毕,下一步可以完成加密计算了,我们用C++实现
移位密码
概述
以 z 26 运算为例 , k 为密钥 加密: e k ( x ) = ( x + k ) m o d 26 解密: d k ( x ) = ( x − k ) m o d 26 以z_{26} 运算为例,k为密钥 \\加密:e_k(x)=(x+k) mod 26 \\解密:d_k(x)=(x-k) mod 26 以z26运算为例,k为密钥加密:ek(x)=(x+k)mod26解密:dk(x)=(x−k)mod26
实际中,我们使用 Z 256 Z_{256} Z256运算(群的加法运算)
代码
#include <iostream> #include <fstream> #include<cstring> using namespace std; int main(){ //加密写入 ofstream fileOut; char helloTxt[]{"&9*&((@#$)((%#^^hello,world!\n123456789"}; int txtLen{strlen(helloTxt)}; fileOut.open("hello.data",ios::binary); int k=77; for(int i=0;i<txtLen;i++){ fileOut<<char((helloTxt[i]+k) %256); } fileOut.close(); //解密读出 ifstream fileIn; char helloChar; fileIn.open("hello.data",ios::binary); while (fileIn.get(helloChar)){ cout<<char((helloChar-k) %256); } fileIn.close(); } &9*&((@#$)((%#^^hello,world! 123456789 Process returned 0 (0x0) execution time : 0.120 s Press any key to continue. 希尔密码( Z 256 Z_{256} Z256)
待加密长度被3整除
#include <iostream> #include <fstream> #include<cstring> #include "e:/eigen/Eigen/Dense" using namespace std; using namespace Eigen; int main(){ //加密写入 ofstream fileOut; char helloTxt[]{"123456789$#%(&Yoiu9"}; int txtLen{strlen(helloTxt)}; fileOut.open("hello.data",ios::binary); for(int i=0;i<txtLen;i+=3){ Matrix<int,1,3> x{helloTxt[i],helloTxt[i+1],helloTxt[i+2]}; Matrix<int,3,3> k{{16,91,215}, {171,253,50}, {8,186,121}}; Matrix<int,1,3> e_data=x*k; for (int j=0;j<3;j++){ fileOut<<char(int(e_data[j]) % 256); } } fileOut.close(); //解密读出 ifstream fileIn; char helloChar; fileIn.open("hello.data",ios::binary); char txtBuffer[4]; for(int i=0;i<txtLen;i+=3){ fileIn.read(txtBuffer,3); Matrix<int,1,3> y{txtBuffer[0],txtBuffer[1],txtBuffer[2]}; Matrix<int,3,3> k_ni{{9,11, 227},{101 ,152 ,37},{134 ,248 ,127}}; Matrix<int,1,3> e_data=y*k_ni; for (int j=0;j<3;j++){ cout<<char(int(e_data[j]) % 256); } } fileIn.close(); } 待加密长度不一定被3整除
继续完善程序,针对加密长度不一定是3的倍数。
#include <iostream> #include <fstream> #include<cstring> #include "e:/eigen/Eigen/Dense" using namespace std; using namespace Eigen; int main(){ //加密写入 ofstream fileOut; char helloTxt[]{"123456789p"}; int txtLen{strlen(helloTxt)}; fileOut.open("hello.data",ios::binary); for(int i=0;i<txtLen;i+=3){ if ((txtLen-i)==1){ Matrix<int,1,3> x{helloTxt[i],0,0}; Matrix<int,3,3> k{{16,91,215}, {171,253,50}, {8,186,121}}; Matrix<int,1,3> e_data=x*k; for (int j=0;j<3;j++){ fileOut<<char(int(e_data[j]) % 256); } } else if ((txtLen-i)==2){ Matrix<int,1,3> x{helloTxt[i],helloTxt[i+1],0}; Matrix<int,3,3> k{{16,91,215}, {171,253,50}, {8,186,121}}; Matrix<int,1,3> e_data=x*k; for (int j=0;j<3;j++){ fileOut<<char(int(e_data[j]) % 256); } } else{ Matrix<int,1,3> x{helloTxt[i],helloTxt[i+1],helloTxt[i+2]}; Matrix<int,3,3> k{{16,91,215}, {171,253,50}, {8,186,121}}; Matrix<int,1,3> e_data=x*k; for (int j=0;j<3;j++){ fileOut<<char(int(e_data[j]) % 256); } } } fileOut.close(); //解密读出 ifstream fileIn; char helloChar; fileIn.open("hello.data",ios::binary); char txtBuffer[4]; for(int i=0;i<txtLen;i+=3){ fileIn.read(txtBuffer,3); Matrix<int,1,3> y{txtBuffer[0],txtBuffer[1],txtBuffer[2]}; Matrix<int,3,3> k_ni{{9,11, 227},{101 ,152 ,37},{134 ,248 ,127}}; Matrix<int,1,3> e_data=y*k_ni; char d_data[3]; for (int j=0;j<3;j++){ d_data[j]=char(int(e_data[j]) % 256); } if ((txtLen-i)==2 ){ cout<<d_data[0]<<d_data[1]; } else if((txtLen-i)==1 ){ cout<<d_data[0]; } else{ for (int j=0;j<3;j++){ cout<<d_data[j]; } } } fileIn.close(); } 123456789p Process returned 0 (0x0) execution time : 0.376 s Press any key to continue. 加解密文件
#include <iostream> #include <fstream> #include<cstring> #include "e:/eigen/Eigen/Dense" using namespace std; using namespace Eigen; int main(){ //加密写入 ifstream picfs("test.png", ios::ate|ios::binary); // 获取文件大小 std::streampos picSize = picfs.tellg(); picfs.close(); // 关闭文件 std::cout << "文件长度: " << picSize << " 字节" << std::endl; ifstream ifs("test.png", ios::in|ios::binary); char *picData=new char[picSize+1]; for (int i=0;i<picSize;i++){ ifs.get(picData[i]); } ifs.close(); int txtLen{picSize}; ofstream fileOut; fileOut.open("pic.dat",ios::binary); for(int i=0;i<txtLen;i+=3){ if ((txtLen-i)==1){ Matrix<int,1,3> x{picData[i],0,0}; Matrix<int,3,3> k{{16,91,215}, {171,253,50}, {8,186,121}}; Matrix<int,1,3> e_data=x*k; for (int j=0;j<3;j++){ fileOut<<char(int(e_data[j]) % 256); } } else if ((txtLen-i)==2){ Matrix<int,1,3> x{picData[i],picData[i+1],0}; Matrix<int,3,3> k{{16,91,215}, {171,253,50}, {8,186,121}}; Matrix<int,1,3> e_data=x*k; for (int j=0;j<3;j++){ fileOut<<char(int(e_data[j]) % 256); } } else{ Matrix<int,1,3> x{picData[i],picData[i+1],picData[i+2]}; Matrix<int,3,3> k{{16,91,215}, {171,253,50}, {8,186,121}}; Matrix<int,1,3> e_data=x*k; for (int j=0;j<3;j++){ fileOut<<char(int(e_data[j]) % 256); } } } fileOut.close(); //解密读出 ofstream deFileOut; deFileOut.open("test_d.png",ios::binary); ifstream fileIn; char helloChar; fileIn.open("pic.dat",ios::binary); char txtBuffer[4]; for(int i=0;i<txtLen;i+=3){ fileIn.read(txtBuffer,3); Matrix<int,1,3> y{txtBuffer[0],txtBuffer[1],txtBuffer[2]}; Matrix<int,3,3> k_ni{{9,11, 227},{101 ,152 ,37},{134 ,248 ,127}}; Matrix<int,1,3> e_data=y*k_ni; char d_data[3]; for (int j=0;j<3;j++){ d_data[j]=char(int(e_data[j]) % 256); } if ((txtLen-i)==2 ){ deFileOut<<d_data[0]<<d_data[1]; } else if((txtLen-i)==1 ){ deFileOut<<d_data[0]; } else{ for (int j=0;j<3;j++){ deFileOut<<d_data[j]; } } } deFileOut.close(); fileIn.close(); delete[] picData; } 迭代密码
概述
- 设K是一个确定长度的随机二元密钥,用K来生成Nr个轮密钥(也叫子密钥) K 1 , K 2 , . . . K N r K^1,K^2,...K^{Nr} K1,K2,...KNr,轮密钥的列表( K 1 , K 2 , . . . K N r K^1,K^2,...K^{Nr} K1,K2,...KNr)就是密钥编排方案,该方案由K经过一个固定的、公开的算法生成。
轮函数 g 由轮密钥 K ′ 和当前状态 w r − 1 作为它的两个输入 , 下一状态为 w r = g ( w r − 1 , K r ) 轮函数g由轮密钥K'和当前状态w^{r-1}作为它的两个输入, \\下一状态为w^r=g(w^{r-1},K^r) 轮函数g由轮密钥K′和当前状态wr−1作为它的两个输入,下一状态为wr=g(wr−1,Kr) - 设 l 和 m 为整数,明文和密文长为 l m 的二元向量 l m 为该密码的分组长度。 S P N 包括两个变换 : 设l和m为整数,明文和密文长为lm的二元向量\\lm为该密码的分组长度。SPN包括两个变换: 设l和m为整数,明文和密文长为lm的二元向量lm为该密码的分组长度。SPN包括两个变换:
1. π S : { 0 , 1 } l → { 0 , 1 } l 2. π P : { 1 , . . . , l m } → { 1 , . . . , l m } 3. 置换 π S 叫 S 盒,用一个 l 比特向量替代另一个 l 比特向量。 置换 π P 用来置换 l m 个比特。 4. 给定一个 l m 比特的二元串 x = ( x 1 , x 2 , . . . . x l m ) 可将其看成 m 个长为 l 比特的子串的 x < 1 > ∣ ∣ . . . ∣ ∣ x < m > 5. 给出的 S P N 由 N r 轮组成,除最后一轮外, 每一轮由异或操作混入该轮的轮密钥, π S 进行 m 次代换, π p 进行一次置换。 1.\pi_S:\{0,1\}^l\rightarrow\{0,1\}^l \\2.\pi_P:\{1,...,lm\}\rightarrow\{1,...,lm\} \\3.置换\pi_S叫S盒,用一个l比特向量替代另一个l比特向量。 \\置换\pi_P用来置换lm个比特。 \\4.给定一个lm比特的二元串x=(x_1,x_2,....x_{lm}) \\可将其看成m个长为l比特的子串的x_{<1>}||...||x_{<m>} \\5.给出的SPN由Nr轮组成,除最后一轮外, \\每一轮由异或操作混入该轮的轮密钥,\pi_S进行m次代换,\pi_p进行一次置换。 1.πS:{0,1}l→{0,1}l2.πP:{1,...,lm}→{1,...,lm}3.置换πS叫S盒,用一个l比特向量替代另一个l比特向量。置换πP用来置换lm个比特。4.给定一个lm比特的二元串x=(x1,x2,....xlm)可将其看成m个长为l比特的子串的x<1>∣∣...∣∣x<m>5.给出的SPN由Nr轮组成,除最后一轮外,每一轮由异或操作混入该轮的轮密钥,πS进行m次代换,πp进行一次置换。
SPN具体算法过程
以下内容由文心一言自动生成
SPN(Substitution-Permutation Network,代换-置换网络)算法是密码学中的一种重要算法模型,广泛应用于分组密码的设计中。SPN算法通过交替进行代换(Substitution)和置换(Permutation)操作来实现数据的加密和解密。下面以一个简化的例子来说明SPN算法的基本过程。
SPN算法基本步骤
初始化:
- 输入:明文(Plaintext)、密钥(Key)和算法参数(如分组长度、轮数等)。
- 预处理:将明文划分为固定长度的分组,通常每个分组包含多个子块(sub-blocks)。同时,从密钥中导出多轮轮密钥(Round Keys)。
加密过程:
- 多轮操作:对明文分组进行多轮(Nr轮)加密操作,每轮包括代换和置换两个步骤。
- 代换(Substitution):在每个子块上应用代换操作。这通常通过查找表(Substitution Box, S-Box)实现,S-Box将输入子块映射到另一个输出子块。代换操作增加了密码算法的混淆性(confusion)。
- 置换(Permutation):对整个分组或分组中的子块进行位置的重新排列。置换操作增加了密码算法的扩散性(diffusion),使得输入中的每一位都影响输出中的多位。
- 轮密钥混合:在每轮加密之前,将轮密钥与当前分组进行混合(如使用异或操作),以引入密钥的影响。
- 多轮操作:对明文分组进行多轮(Nr轮)加密操作,每轮包括代换和置换两个步骤。
输出:
- 经过Nr轮加密后,输出密文(Ciphertext)。
举例说明
假设有一个简化的SPN算法,分组长度为16位(2个字节),每个分组被划分为两个8位的子块。算法进行两轮加密,使用简单的S-Box和P-Box(置换盒)。
明文:假设明文分组为 0x12345678(十六进制表示,等价于二进制 00010010 00110100 01010110 01111000)。
密钥和轮密钥:这里假设初始密钥为 0xABCDEF,通过某种密钥扩展算法(如密钥调度算法)生成两轮轮密钥,分别为 0xABCD 和 0xEF00(仅为示例,实际中轮密钥的生成会更复杂)。
第一轮加密:
- 轮密钥混合:将第一轮轮密钥
0xABCD与明文分组进行异或操作。- 假设操作后结果为
0xXYZW1234(此处XYZW为异或后的结果,具体值取决于密钥和明文)。
- 假设操作后结果为
- 代换:将
0xXYZW和1234分别作为两个子块,通过S-Box进行代换。- 假设代换后结果为
0xA1B2C3D4和0x5678E9F0。
- 假设代换后结果为
- 置换:对整个16位分组进行置换操作。
- 假设置换后结果为
0x56A178B2E9C3F0D4。
- 假设置换后结果为
第二轮加密(过程与第一轮类似,但使用第二轮轮密钥):
- 轮密钥混合、代换、置换。
- 最终得到密文
0x...(具体值取决于算法的具体实现)。
- 最终得到密文
注意
- 上述例子仅为说明SPN算法的基本过程,实际中的SPN算法(如AES等)会更为复杂,包括更多的轮数、更复杂的S-Box和P-Box设计、以及更复杂的密钥扩展算法。
- S-Box和P-Box的具体实现是SPN算法的关键部分,它们的设计直接影响算法的安全性和性能。
- 在实际应用中,SPN算法通常与密钥扩展算法、初始化向量(IV)等结合使用,以提供更高级别的安全性。
轮换-置换网络
以下内容由文心一言自动生成
代换-置换网络(Substitution-Permutation Network,简称SPN或SP-network)是密码学中的一种重要概念,特别是在分组密码的设计中。它由美国数学家克劳德·香农在1949年提出,旨在通过简单的代换和置换操作组合,实现安全的加密方式。以下是对代换-置换网络的详细解释:
一、定义与概述
代换-置换网络是一系列被应用于分组密码中的数学运算,它通过交错的若干“轮”(或“层”)代换操作和置换操作,将明文块和密钥块作为输入,最终产生密文块。这种加密方法因其高效性和在硬件上的易实现性而得到广泛应用。
二、核心组件
代换-置换网络主要包括两个核心组件:代换(Substitution)和置换(Permutation),它们分别被称为S盒(替换盒,S-boxes)和P盒(排列盒,P-boxes)。
代换(Substitution):代换操作是将输入数据块中的每个元素(通常是字节或比特)按照一定的规则替换为另一个元素。在SPN中,这通常通过S盒实现,S盒是一个查找表,它定义了输入到输出的映射关系。
置换(Permutation):置换操作是对数据块中的元素进行重新排列,而不改变它们的值。在SPN中,这通过P盒实现,P盒定义了元素在数据块中的新位置。
三、加密过程
代换-置换网络的加密过程通常包括多个轮次,每轮都包含代换、置换和轮密钥混合(通常为异或操作)三个步骤。具体过程如下:
初始密钥扩展:首先,使用密钥扩展算法(也称为密钥编排算法)将输入的单个密钥扩展为多个子密钥,每个子密钥用于一轮加密。
代换操作:在每一轮中,首先使用当前轮的子密钥与明文块(或上一轮的密文块)进行某种形式的混合(如异或操作),然后对结果进行代换操作,即使用S盒替换数据块中的元素。
置换操作:接着,对代换后的结果进行置换操作,即使用P盒重新排列数据块中的元素。
轮密钥混合:最后,将置换后的结果与当前轮的子密钥进行再次混合(如异或操作),生成该轮的密文块。该密文块将作为下一轮的输入(如果有多轮加密的话)。
四、应用实例
代换-置换网络因其高效性和安全性,在多种分组密码标准中得到了广泛应用。例如,高级加密标准(AES)就是基于代换-置换网络设计的。AES使用了一个或多个S盒和P盒,通过多轮迭代加密,实现了对数据的安全保护。
五、总结
代换-置换网络是密码学中的一种重要加密方法,它通过交错的代换和置换操作,以及轮密钥混合,实现了对明文块的安全加密。由于其高效性和在硬件上的易实现性,代换-置换网络在分组密码的设计中得到了广泛应用。
轮函数理论
以下内容由文心一言自动生成
在密码学中,轮函数(Round Function)是一个关键概念,特别是在分组密码和Feistel网络中尤为重要。以下是对轮函数的详细解释:
定义与作用
轮函数是密码算法中的一个重要组成部分,它负责在每一轮加密或解密过程中对数据进行处理。在Feistel网络中,轮函数的作用尤为显著,它根据“右侧”数据和子密钥生成对“左侧”数据进行加密的比特序列,然后将“左侧”数据与该比特序列进行异或(XOR)运算,从而得到“加密后的左侧”。这一过程是迭代进行的,每一轮都会使用新的子密钥或经过变换的密钥。
特点与性质
- 可迭代性:轮函数的设计允许算法进行多轮迭代,以提高加密的安全性。在Feistel网络中,加密和解密的轮数可以任意增加,而不会导致无法解密的情况。
- 可逆性:轮函数通常是可逆的,这意味着在解密过程中可以使用相同的轮函数(或其逆函数)来恢复原始数据。然而,在Feistel网络中,解密过程并不直接依赖于轮函数的逆函数,而是通过反向迭代和异或运算来实现。
- 复杂性:轮函数的设计通常具有一定的复杂性,以抵御各种密码分析攻击。这包括使用非线性函数、置换操作、混淆和扩散等技术来确保数据的机密性和完整性。
应用实例
轮函数在多种密码算法中都有应用,其中最著名的例子之一是DES(数据加密标准)算法。DES算法采用了Feistel网络结构,其中轮函数是关键组成部分。在DES中,轮函数接收两个输入参数:分组数据(原始数据的一半)和子密钥,然后生成和分组数据同样长度的数据。这个数据随后与原始数据的另一半进行异或运算,作为下一轮轮函数的输入。
除了DES之外,还有许多其他算法也采用了轮函数的概念,如AES(高级加密标准)、Blowfish、Twofish等。这些算法在轮函数的设计和实现上各有特色,但都遵循了类似的加密和解密原理。
总结
轮函数是密码学中的一个重要概念,它在分组密码和Feistel网络中发挥着关键作用。通过迭代使用轮函数,密码算法可以实现对数据的多次加密和解密操作,从而提高加密的安全性和可靠性。在设计轮函数时,需要考虑其可迭代性、可逆性和复杂性等因素,以确保算法能够抵御各种密码分析攻击。
迭代密码理论
以下内容由文心一言自动生成
迭代密码,也被称为迭代分组密码,是一种常见的密码算法。其基本原理是将明文分成固定长度的数据块,对每个数据块进行加密,最终得到密文。在迭代分组密码中,加密算法通常是一种置换加密算法,其中包含多个轮次。以下是对迭代密码的详细解释:
定义与原理
- 定义:迭代密码是一种特殊的乘积密码,其中密文C由明文P通过多轮加密得到。每一轮中,数据块会与一个密钥(可能是轮密钥或固定的主密钥)进行加密运算,并生成一个中间结果。然后,这个中间结果会作为下一轮的输入,再次与密钥进行加密运算。这一过程会重复多次,直到最后一轮结束,得到最终的密文。
- 原理:迭代密码的安全性基于其多轮加密的复杂性。通过多轮加密,即使每一轮使用的加密算法相对简单,整个迭代密码系统的安全性也能得到显著提升。这是因为攻击者需要破解每一轮的加密,才能最终恢复出明文。
特点与优势
- 安全性高:迭代密码能够抵御多种攻击方式,包括暴力破解、差分密码分析、线性密码分析等。
- 灵活性好:迭代密码可以根据需要调整轮数、密钥长度等参数,以适应不同的安全需求。
- 易于实现:迭代密码的算法相对简单,易于在硬件和软件上实现。
应用场景
迭代密码广泛应用于各种需要加密保护的场景,包括网络通信、数据存储、电子商务等。例如,在网络通信中,迭代密码可以用于保护传输数据的机密性和完整性;在数据存储中,迭代密码可以用于加密存储在硬盘、闪存等介质上的敏感数据;在电子商务中,迭代密码可以用于保护用户的个人信息和交易数据。
示例
以AES(高级加密标准)为例,AES是一种广泛使用的迭代分组密码算法。它采用固定长度的数据块(通常为128位)和可变长度的密钥(128位、192位或256位)进行加密。AES算法包含多个轮次(通常为10轮、12轮或14轮),每一轮中都会使用不同的子密钥和变换函数对数据进行加密。通过这种方式,AES能够提供极高的安全性和灵活性。
发展趋势
随着计算机技术和密码学的发展,迭代密码也在不断演进。一方面,新的加密算法和技术的出现为迭代密码提供了更多的选择和可能性;另一方面,随着计算能力的提升和攻击技术的发展,迭代密码也面临着更大的挑战。因此,未来的迭代密码算法将更加注重安全性、效率和灵活性之间的平衡,以适应不断变化的安全需求和技术环境。
AES
特点
- AES是迭代型密码。
- 轮数取决于密钥的长度,128位密钥为10轮,192位为12轮,256位为14轮
- 算法基本过程
1.给明文x,设state=x
2.AddRoundKey(state)
3.对前Nr-1轮中的每一轮
(1)用S盒对state进行一次代换SubBytes
(2)对state进行置换ShiftRows
(3)对state进行MixColumns
(4)对state进行AddRoundKey
4.最后一轮,依次进行SubBytes、ShiftRows、MixColumns后的state为密文
以下内容由文心一言自动生成
概述
AES(Advanced Encryption Standard)算法是一种广泛使用的对称加密算法,它以其高效性和安全性而闻名。以下是对AES算法的详细解析:
一、算法概述
- 类型:对称加密算法,即加密和解密使用相同的密钥。
- 分组长度:AES算法将明文分成固定长度的分组进行加密,每个分组长度为128位(16字节)。
- 密钥长度:支持三种密钥长度,分别是128位、192位和256位。不同长度的密钥会影响加密的轮数和安全性。
二、加密过程
AES加密过程包括密钥扩展、初始轮和多个重复轮(包括SubBytes、ShiftRows、MixColumns和AddRoundKey操作,但最后一轮省略MixColumns)。
1. 密钥扩展(Key Expansion)
- 输入:原始密钥。
- 过程:通过复杂的函数(密钥扩展函数)和轮常量(Rcon),结合S盒进行字节替换和异或操作,生成多个轮密钥。
- 输出:多个轮密钥,用于后续加密过程。
2. 初始轮(AddRoundKey)
- 输入:原始明文和第一个轮密钥(实际上是原始密钥)。
- 过程:将明文和轮密钥进行逐字节异或操作。
- 输出:经过异或操作后的数据,作为第一轮加密的输入。
3. 重复轮(多个轮次)
- SubBytes(字节代换):使用S盒对状态矩阵中的每个字节进行代换,增加数据的混乱性。
- ShiftRows(行移位):将状态矩阵的行进行循环移位,改变数据的排列方式。
- MixColumns(列混合):在除了最后一轮之外的每一轮中,将状态矩阵的列与一个固定的多项式进行乘法操作,增加数据的扩散性。
- AddRoundKey:将当前状态与轮密钥进行异或操作,得到加密后的状态。
对于AES-128,除了最后一轮外,其他轮次都包括SubBytes、ShiftRows、MixColumns三个步骤。最后一轮省略MixColumns步骤。
三、解密过程
AES解密过程是加密过程的逆过程,使用相同的密钥但逆序执行操作(InvSubBytes、InvShiftRows、InvMixColumns)。
- InvSubBytes:使用逆S盒进行字节替换的逆操作。
- InvShiftRows:进行行移位的逆操作。
- InvMixColumns:进行列混合的逆操作(在解密过程中,除了第一轮外都需要执行)。
- AddRoundKey:与加密过程相同,将当前状态与轮密钥进行异或操作。
四、算法特点
- 高效性:AES算法设计精巧,能够在多种平台上实现高效加密。
- 安全性:AES算法采用了高度复杂的算法结构,包括字节替换、行移位、列混淆等多重操作,使得攻击者很难找到有效的攻击路径。同时,AES算法支持不同长度的密钥,密钥长度越长,加密强度越高。
- 灵活性:AES算法支持多种加密模式(如ECB、CBC、CFB、OFB和CTR模式),可以根据不同的应用场景选择适合的加密模式。
五、应用领域
AES算法因其高效性和安全性而被广泛应用于各种领域,如网络通信、数据存储、电子支付等。它是许多安全标准和协议的重要组成部分,如TLS/SSL协议、IPsec协议等。
综上所述,AES算法是一种高效、安全且灵活的对称加密算法,其详细的加密和解密过程体现了其复杂性和安全性。
算法过程
AES(Advanced Encryption Standard)算法是一种广泛使用的对称加密算法,其过程可以详细分为密钥扩展、初始轮以及多个重复轮(包括SubBytes、ShiftRows、MixColumns,最后一轮省略MixColumns)等步骤。以下是AES算法过程的具体描述:
1. 密钥扩展(Key Expansion)
- 输入:原始密钥(对于AES-128,是128位长的密钥)。
- 过程:
- 将原始密钥分为几个部分(对于AES-128,通常分为4个32位的部分)。
- 使用一个复杂的函数(密钥扩展函数),结合轮常量(Rcon)和S盒(Substitution Box)进行字节替换和异或操作,生成多个轮密钥。
- 轮密钥的数量取决于密钥的长度和加密轮数(AES-128需要10轮,因此生成10+1=11个轮密钥,因为第一个轮密钥是原始密钥)。
- 输出:多个轮密钥,用于后续的加密过程。
2. 初始轮(AddRoundKey)
- 输入:原始明文(plaintext)和第一个轮密钥(实际上是原始密钥,因为AES的初始轮使用原始密钥作为轮密钥)。
- 过程:
- 将明文和轮密钥(在初始轮中是原始密钥)进行逐字节的异或(XOR)操作。
- 输出:经过异或操作后的数据,作为第一轮加密的输入。
3. 重复轮(多个轮次)
对于AES-128,除了最后一轮外,其他轮次都包括SubBytes、ShiftRows、MixColumns三个步骤。
- SubBytes(字节代换):
- 使用S盒对每个字节进行替换。S盒是一个预定义的替换表,用于将输入字节映射到另一个字节。
- 替换过程是可逆的,即存在逆S盒用于解密。
- ShiftRows(行移位):
- 将状态矩阵(一个4x4的字节矩阵)的行进行循环移位。
- 第一行保持不变,第二行左移一个字节,第三行左移两个字节,第四行左移三个字节。
- 解密过程中,行移位是逆操作,即右移相应数量的字节。
- MixColumns(列混合):
- 在除了最后一轮之外的每一轮中,将状态矩阵的列与一个固定的多项式进行乘法操作(在有限域上)。
- 列混合操作增加了数据的扩散性,使得单个明文字节的变化能够影响到整个密文块。
- 解密过程中,存在逆列混合操作。
4. 最终轮
- SubBytes:与前面轮次相同,使用S盒进行字节替换。
- ShiftRows:与前面轮次相同,进行行移位。
- AddRoundKey:与初始轮相似,但使用的是最后一个轮密钥。将当前状态与最后一个轮密钥进行异或操作,得到最终的密文。
5. 输出
- 输出:加密后的密文。
注意事项
- AES算法的解密过程是加密过程的逆过程,使用相同的密钥但逆序执行操作(InvSubBytes、InvShiftRows、InvMixColumns)。
- AES算法的安全性部分来自于其多轮迭代的结构,每一轮都通过不同的方式混淆和扩散数据。
- AES算法的高效性和安全性使其成为现代加密技术的基石,广泛应用于各种安全领域。
以上信息基于AES算法的标准描述和广泛接受的实现方式。需要注意的是,具体的实现细节(如密钥扩展函数的具体实现)可能因不同的实现或库而异。
S盒
下面内容来自文心一言的自动生成
AES(Advanced Encryption Standard,高级加密标准)中的S盒(Substitution Box)是AES算法的核心组件之一,它在加密和解密过程中起着至关重要的作用。以下是关于AES的S盒的详细解释:
1. S盒的定义与功能
- 定义:S盒是一个固定的字节替代表,用于替换输入的字节值。它是一个16x16的字节矩阵,包含了8位所能表示的256个数的一个置换。
- 功能:S盒的主要功能是实现非线性的字节替换,增加算法的复杂度,从而提高加密的安全性。
2. S盒的构造
- 初始化:S盒按字节值的升序逐行初始化,即每个值都代表了坐标。
- 映射规则:State中每个字节按照其高4位作为行值,低4位作为列值,以这些数值为索引从S盒的对应位置取出元素作为输出。例如,十六进制数{95}所对应的S盒行值是9,列值是5,S盒中在此位置的值是{2A},因此{95}被映射为{2A}。
- 变换过程:S盒的构造涉及到GF(2^8)的乘法逆和矩阵的可逆运算。具体来说,把S盒中的每个字节的8个构成位记为(b7,b6,b5,b4,b3,b2,b1,b0),并对每个字节的每个位进行特定的变换,以生成最终的S盒。
3. S盒的特点
- 非线性:S盒是非线性的,这意味着相同的输入不会总是产生相同的输出,这有助于抵抗统计分析和线性攻击。
- 可逆性:S盒是可逆的,即存在逆S盒可以将S盒的输出映射回原始输入,这是解密过程所必需的。
- 固定性:AES中的S盒是固定的,不依赖于特定的密钥或明文。
4. S盒在AES中的作用
- 混淆:S盒通过替换输入字节的值,增加了数据的混淆性,使得攻击者难以从密文中推断出明文的信息。
- 扩散:虽然S盒本身不直接提供扩散性(即一个字节的变化会影响多个字节的输出),但它与其他AES变换(如行移位和列混淆)一起工作,共同实现数据的扩散。
5. 与DES S盒的比较
- 大小与输入输出:AES的S盒是16x16的字节矩阵,输入和输出的位数相同,均为8位(即1字节)。而DES的S盒大小是4x16的位矩阵,输入6位,输出4位。
- 数量:AES只有一个S盒,而DES有8个不同的S盒。
- 设计理念:AES的S盒设计注重可逆性和非线性,而DES的S盒设计主要是为了确保非线性关系,并不要求可逆。
综上所述,AES的S盒是AES算法中不可或缺的一部分,它通过非线性的字节替换增加了加密的复杂性和安全性。
GF域
下面内容来自文心一言的自动生成
域
在数学中,域(Field)是一个重要的代数结构,具有特定的性质和运算规则。以下是对数学中域的详细解释:
一、定义
在数学中,域是对加、减、乘、除(除数不为0)都封闭的代数结构。具体来说,如果F是一个集合,并且在其上定义了加法和乘法两种运算,且满足以下条件,则称F为一个域:
- 加法封闭性:对于F中的任意两个元素a和b,它们的和a+b仍然是F中的元素。
- 乘法封闭性:对于F中的任意两个元素a和b,它们的积ab仍然是F中的元素。
- 加法单位元:F中存在一个元素0(称为加法单位元或零元),使得对于F中的任意元素a,都有a+0=a。
- 加法逆元:对于F中的任意非零元素a,都存在一个元素-a(称为a的加法逆元或负元),使得a+(-a)=0。
- 乘法单位元:F中存在一个元素1(称为乘法单位元或幺元),使得对于F中的任意元素a(a≠0),都有a×1=a。
- 乘法逆元:对于F中的任意非零元素a,都存在一个元素a(-1)(称为a的乘法逆元或倒数),使得a×a(-1)=1。
- 交换律:加法和乘法都满足交换律,即对于F中的任意两个元素a和b,都有a+b=b+a和a×b=b×a。
- 结合律:加法和乘法都满足结合律,即对于F中的任意三个元素a、b和c,都有(a+b)+c=a+(b+c)和(a×b)×c=a×(b×c)。
- 分配律:乘法对加法满足分配律,即对于F中的任意三个元素a、b和c,都有a×(b+c)=a×b+a×c。
二、常见域
- 有理数域Q:由所有有理数组成的集合,包括整数、分数等,对加、减、乘、除(除数不为0)都封闭。
- 实数域R:由所有实数组成的集合,包括有理数和无理数(如π、e等),对加、减、乘、除(除数不为0)都封闭。
- 复数域C:由所有复数组成的集合,可以表示为a+bi的形式(其中a,b为实数,i为虚数单位),对加、减、乘、除(除数不为0)都封闭。
三、性质与应用
- 性质:域具有许多重要的性质,如封闭性、可逆性、交换性、结合性和分配性等。这些性质使得域成为研究代数结构的基础。
- 应用:域论在数学、物理学、计算机科学、密码学等多个领域都有广泛的应用。例如,在数论中,域论可以用来解决关于数的性质和关系的问题;在密码学中,域论被用于构建安全高效的加密算法;在计算机科学中,域论被用于设计算法和数据结构等。
四、扩展与深化
- 域扩张:在已有的域的基础上,可以通过添加新的元素来构造更大的域,称为域的扩张。例如,有理数域可以通过扩张得到实数域和复数域。
- 有限域:除了上述的无限域外,还存在有限域(也称为Galois域),其元素数量是有限的。有限域在编码理论、密码学等领域中有重要的应用。
综上所述,数学中的域是一个具有特定性质和运算规则的代数结构,它在多个领域都有广泛的应用。
GF概述
GF域,即Galois Field,也称为有限域,是一个其元素数量有限的域。以下是关于GF域的详细解释:
一、定义与表示
- 定义:有限域是一个其元素数量有限的域。域是一个代数结构,包含一组元素以及加法和乘法两种运算,且满足一定的运算规则(如结合律、交换律、分配律等)。
- 表示:有限域的阶(元素数量)是素数p的幂,即 p n p^n pn,其中n是正整数。阶为p的有限域一般表示为GF§,阶为 p n p^n pn的表示为 G F ( p n ) GF(p^n) GF(pn)。“GF”代表Galois域,以第一位研究有限域的数学家Evariste Galois命名。
二、重要性质
- 元素数量: G F ( p n ) 包含 p n 个元素 GF(p^n)包含p^n个元素 GF(pn)包含pn个元素。
- 运算规则:
- 加法: 在 G F ( p n ) 中,加法是模 p n 的加法,但通常由于 n > 1 时直接模 p n 并不直观,因此会通过多项式或其他方式来表示 G F ( p n ) 中的元素和加法 在GF(p^n)中,加法是模p^n的加法,但通常由于n>1时直接模p^n并不直观,因此会通过多项式或其他方式来表示GF(p^n)中的元素和加法 在GF(pn)中,加法是模pn的加法,但通常由于n>1时直接模pn并不直观,因此会通过多项式或其他方式来表示GF(pn)中的元素和加法。
- 乘法: 乘法同样需要满足域的性质,且在 G F ( p n ) 中,乘法逆元的存在性保证了除法的可定义性 乘法同样需要满足域的性质,且在GF(p^n)中,乘法逆元的存在性保证了除法的可定义性 乘法同样需要满足域的性质,且在GF(pn)中,乘法逆元的存在性保证了除法的可定义性。
- 乘法逆元: 在 G F ( p n ) 中,除了 0 以外的每个元素都有乘法逆元 在GF(p^n)中,除了0以外的每个元素都有乘法逆元 在GF(pn)中,除了0以外的每个元素都有乘法逆元。
三、构造与扩展
- 基域与扩展域: G F ( p ) 称为 G F ( p m ) 的基域, G F ( p m ) 称为 G F ( p ) 的扩展域。扩展域的构造通常从本原多项式开始,通过本原多项式的根来构造 G F ( p m ) 中的元素 GF(p)称为GF(p^m)的基域,GF(p^m)称为GF(p)的扩展域。扩展域的构造通常从本原多项式开始,通过本原多项式的根来构造GF(p^m)中的元素 GF(p)称为GF(pm)的基域,GF(pm)称为GF(p)的扩展域。扩展域的构造通常从本原多项式开始,通过本原多项式的根来构造GF(pm)中的元素。
- 本原多项式: 在 G F ( p ) 上,一个 m 阶多项式如果既不能被 G F ( p ) 上的任何非零多项式整除,又能整除 X ( p m ) − X ,则称该多项式为 G F ( p ) 上的 m 阶本原多项式。本原多项式对于构造 G F ( p m ) 至关重要 在GF(p)上,一个m阶多项式如果既不能被GF(p)上的任何非零多项式整除,又能整除X^(p^m)-X,则称该多项式为GF(p)上的m阶本原多项式。本原多项式对于构造GF(p^m)至关重要 在GF(p)上,一个m阶多项式如果既不能被GF(p)上的任何非零多项式整除,又能整除X(pm)−X,则称该多项式为GF(p)上的m阶本原多项式。本原多项式对于构造GF(pm)至关重要。
四、应用
GF域在多个领域都有广泛的应用,特别是在纠错码和密码学领域。例如,BCH码和RS码等纠错码就是基于GF域构造的。此外,GF域在密码算法中也扮演着重要角色,如用于椭圆曲线密码学中的点乘运算等。
五、示例
- GF(2):最简单的有限域,其元素为{0,1},加法等价于异或(XOR)运算,乘法等价于逻辑与(AND)运算。
- GF(7):阶为7的域,使用模7运算。其元素为{0,1,2,3,4,5,6},并定义了相应的加法和乘法运算规则。
六、结论
GF域作为有限域的一种表示方式,在数学、计算机科学、密码学等多个领域都有广泛的应用。通过对其定义、性质、构造和应用的深入了解,可以更好地理解这一重要概念。
详细解释
GF域,全称为Galois Field,也称为有限域(Finite Field),是数学中一种特殊的代数结构,对于密码学、编码理论等领域有着重要的应用。以下是对GF域的详细解释:
一、定义
GF域是一个包含有限个元素的集合,这些元素之间定义了加法和乘法两种运算,且满足以下性质:
- 封闭性:对于GF域中的任意两个元素,它们的和与积仍然是GF域中的元素。
- 结合律:加法和乘法都满足结合律。
- 交换律:加法和乘法都满足交换律。
- 分配律:乘法对加法满足分配律。
- 单位元:存在加法单位元(通常记为0)和乘法单位元(通常记为1)。
- 逆元: 对于 G F 域中的任意非零元素 a ,都存在一个加法逆元 − a 和一个乘法逆元 a − 1 ,使得 a + ( − a ) = 0 且 a ∗ a − 1 = 1 对于GF域中的任意非零元素a,都存在一个加法逆元-a和一个乘法逆元a^{-1},使得a+(-a)=0且a*a^{-1}=1 对于GF域中的任意非零元素a,都存在一个加法逆元−a和一个乘法逆元a−1,使得a+(−a)=0且a∗a−1=1。
二、特点
- 元素个数有限:GF域的元素个数是有限的,通常用GF(q)表示一个含有q个元素的有限域。
- 运算特殊性:GF域中的加法和乘法运算可能与我们日常使用的运算不同。例如,在GF(2^n)中,加法通常定义为异或运算(XOR),乘法则是基于模多项式运算的。
- 素域与扩展域:GF§称为素域,其中p是一个素数。GF(p^n)是GF§的扩展域,其中n是一个正整数。
三、运算规则
- 加法: 在 G F ( 2 n ) 中,加法通常定义为异或运算。例如,在 G F ( 2 3 ) 中,多项式 f ( x ) = x 2 + x + 1 与 g ( x ) = x 2 + 1 相加得到的结果为 h ( x ) = x + 1 ,因为 x 2 + x + 1 X O R x 2 + 1 = x + 1 (注意这里的 X O R 是逐位进行的 ) 在GF(2^n)中,加法通常定义为异或运算。例如,在GF(2^3)中,多项式f(x)=x^2+x+1与g(x)=x^2+1相加得到的结果为h(x)=x+1,因为x^2+x+1 XOR x^2+1 = x+1(注意这里的XOR是逐位进行的) 在GF(2n)中,加法通常定义为异或运算。例如,在GF(23)中,多项式f(x)=x2+x+1与g(x)=x2+1相加得到的结果为h(x)=x+1,因为x2+x+1XORx2+1=x+1(注意这里的XOR是逐位进行的)。
- 乘法: 乘法运算则较为复杂,通常涉及模多项式运算。在 G F ( 2 n ) 中,选择一个 n 次不可约多项式作为模多项式,所有运算都在该多项式下进行。例如,在 G F ( 2 8 ) 中,常用的模多项式为 x 8 + x 4 + x 3 + x + 1 乘法运算则较为复杂,通常涉及模多项式运算。在GF(2^n)中,选择一个n次不可约多项式作为模多项式,所有运算都在该多项式下进行。例如,在GF(2^8)中,常用的模多项式为x^8+x^4+x^3+x+1 乘法运算则较为复杂,通常涉及模多项式运算。在GF(2n)中,选择一个n次不可约多项式作为模多项式,所有运算都在该多项式下进行。例如,在GF(28)中,常用的模多项式为x8+x4+x3+x+1。
四、应用
GF域在多个领域都有重要的应用,包括但不限于:
- 密码学:在加密算法中,GF域被用于限制数字的范围,提高算法的安全性和效率。例如,AES加密算法中的列混淆步骤就使用了GF(2^8)域。
- 编码理论:GF域是构建纠错码(如BCH码、RS码)的重要基础。通过GF域上的多项式运算,可以实现数据的冗余编码,提高数据传输的可靠性。
- 数字信号处理:在数字信号处理中,GF域可以用于设计滤波器、实现快速傅里叶变换等。
五、实例
以GF(2^3)为例,其元素可以表示为0, 1, x, x+1, x^2, x^2+1, x^2+x, x2+x+1(其中x是一个抽象元素,满足x3=x+1,这是由模多项式x3+x+1决定的)。在这个域中,我们可以进行加法和乘法运算,如(x+1)+(x2+x)=x2+1(异或运算),(x+1)*(x2+1)=x2+x+x+1=x2+1(模多项式运算)。
综上所述,GF域是一种具有特殊性质和运算规则的有限代数结构,在多个领域都有广泛的应用。
伽罗瓦域(Galois Field)
下面内容来自文心一言的自动生成
又称为有限域(Finite Field)或GF域,是数学中一种重要的代数结构,它在密码学、编码理论、计算机科学等多个领域有着广泛的应用。以下是对伽罗瓦域的详细解释:
零、2是素数吗
2是素数。素数是指只能被1和它本身整除的大于1的自然数。在这个定义下,2只能被1和2整除,没有其他正除数,因此它满足素数的定义。所以,2是素数。
一、定义
伽罗瓦域是一个包含有限个元素的集合,这些元素之间定义了加法和乘法两种运算,且满足域的所有性质:封闭性、结合律、交换律、分配律、存在单位元和逆元等。伽罗瓦域的元素数量是某一素数p的幂,即pn(p是素数,n是正整数),因此常用GF(pn)来表示p^n元的伽罗瓦域。
二、性质
- 有限性:伽罗瓦域的元素数量是有限的,这是它与其他无限域(如实数域、复数域)的主要区别。
- 封闭性:伽罗瓦域中的加法和乘法运算都是封闭的,即任意两个元素的和与积仍然是伽罗瓦域中的元素。
- 运算规则:伽罗瓦域中的加法和乘法运算满足域的所有运算规则,包括结合律、交换律、分配律等。
- 单位元和逆元:伽罗瓦域中存在加法单位元(通常记为0)和乘法单位元(通常记为1),且对于域中的任意非零元素a,都存在一个加法逆元-a和一个乘法逆元a^-1。
- 特征数:伽罗瓦域的特征数必为某一素数p,即域中所有非零元素的加法阶数都是p的倍数。
三、构造与表示
- 素域: G F ( p ) 是伽罗瓦域的一个特例,称为素域,其中 p 是一个素数。素域是所有伽罗瓦域的基础 GF(p)是伽罗瓦域的一个特例,称为素域,其中p是一个素数。素域是所有伽罗瓦域的基础 GF(p)是伽罗瓦域的一个特例,称为素域,其中p是一个素数。素域是所有伽罗瓦域的基础。
- 扩展域: G F ( p n ) 是 G F ( p ) 的扩展域,其中 n 是一个正整数。扩展域的元素可以通过素域中的元素和多项式来表示 GF(p^n)是GF(p)的扩展域,其中n是一个正整数。扩展域的元素可以通过素域中的元素和多项式来表示 GF(pn)是GF(p)的扩展域,其中n是一个正整数。扩展域的元素可以通过素域中的元素和多项式来表示。
- 多项式表示: 在 G F ( 2 n ) 等特定情况下,域中的元素常用二进制多项式来表示。这些多项式是在某个 n 次不可约多项式(称为模多项式)下定义的,所有运算都在该多项式下进行 在GF(2^n)等特定情况下,域中的元素常用二进制多项式来表示。这些多项式是在某个n次不可约多项式(称为模多项式)下定义的,所有运算都在该多项式下进行 在GF(2n)等特定情况下,域中的元素常用二进制多项式来表示。这些多项式是在某个n次不可约多项式(称为模多项式)下定义的,所有运算都在该多项式下进行。
四、运算规则
- 加法: 在 G F ( 2 n ) 等特定情况下,加法通常定义为异或运算( X O R )。异或运算满足交换律和结合律,且对于任意元素 a ,都有 a + 0 = a 和 a + a = 0 (即 a 的加法逆元是 a 本身) 在GF(2^n)等特定情况下,加法通常定义为异或运算(XOR)。异或运算满足交换律和结合律,且对于任意元素a,都有a+0=a和a+a=0(即a的加法逆元是a本身) 在GF(2n)等特定情况下,加法通常定义为异或运算(XOR)。异或运算满足交换律和结合律,且对于任意元素a,都有a+0=a和a+a=0(即a的加法逆元是a本身)。
- 乘法: 乘法运算则较为复杂,通常涉及模多项式运算。在 G F ( 2 n ) 中,选择一个 n 次不可约多项式作为模多项式,所有乘法运算都在该多项式下进行。乘法运算满足结合律、交换律和分配律,且对于任意非零元素 a ,都存在一个乘法逆元 a − 1 使得 a ∗ a − 1 = 1 乘法运算则较为复杂,通常涉及模多项式运算。在GF(2^n)中,选择一个n次不可约多项式作为模多项式,所有乘法运算都在该多项式下进行。乘法运算满足结合律、交换律和分配律,且对于任意非零元素a,都存在一个乘法逆元a^-1使得a*a^-1=1 乘法运算则较为复杂,通常涉及模多项式运算。在GF(2n)中,选择一个n次不可约多项式作为模多项式,所有乘法运算都在该多项式下进行。乘法运算满足结合律、交换律和分配律,且对于任意非零元素a,都存在一个乘法逆元a−1使得a∗a−1=1。
五、应用领域
伽罗瓦域在多个领域都有重要的应用:
- 密码学:在加密算法中,伽罗瓦域被用于限制数字的范围和提高算法的安全性。例如,AES加密算法中的列混淆步骤就使用了 G F ( 2 8 ) GF(2^8) GF(28)域。
- 编码理论:伽罗瓦域是构建纠错码(如BCH码、RS码)的重要基础。通过伽罗瓦域上的多项式运算,可以实现数据的冗余编码和高效纠错。
- 数字信号处理:在数字信号处理中,伽罗瓦域可以用于设计滤波器、实现快速傅里叶变换等。
- 计算机科学:在计算机科学中,伽罗瓦域被用于设计算法和数据结构等。例如,在有限域上的乘法运算可以用于实现某些类型的哈希函数和随机数生成器。
综上所述,伽罗瓦域是一种具有特殊性质和运算规则的有限代数结构,在数学、密码学、编码理论、计算机科学等多个领域都有广泛的应用。
GF(28)域,即有限域GF(28),是一个包含256个元素的有限域,其中每个元素可以表示为0到255之间的整数,也可以表示为8位二进制数(或等价的二进制多项式)。这个域在密码学、编码理论、计算机科学等领域有着广泛的应用。以下是对GF(2^8)域的详细解释:
GF(2^8)域
下面内容来自文心一言的自动生成
一、定义与性质
- 定义: G F ( 2 8 ) 是一个由 2 8 = 256 个元素构成的有限域,其中的元素可以表示为 0 到 255 的整数或 8 位二进制数 GF(2^8)是一个由2^8=256个元素构成的有限域,其中的元素可以表示为0到255的整数或8位二进制数 GF(28)是一个由28=256个元素构成的有限域,其中的元素可以表示为0到255的整数或8位二进制数。
- 性质:
- 封闭性: G F ( 2 8 ) 域中的加法和乘法运算都是封闭的,即任意两个元素的和与积仍然是 G F ( 2 8 ) 域中的元素 GF(2^8)域中的加法和乘法运算都是封闭的,即任意两个元素的和与积仍然是GF(2^8)域中的元素 GF(28)域中的加法和乘法运算都是封闭的,即任意两个元素的和与积仍然是GF(28)域中的元素。
- 结合律与交换律:加法和乘法运算都满足结合律和交换律。
- 分配律:乘法对加法满足分配律。
- 单位元与逆元: 存在加法单位元( 0 )和乘法单位元( 1 ),且对于域中的任意非零元素 a ,都存在一个加法逆元 − a (在 G F ( 2 8 ) 中 − a 等于 a 本身,因为加法是异或运算)和一个乘法逆元 a − 1 存在加法单位元(0)和乘法单位元(1),且对于域中的任意非零元素a,都存在一个加法逆元-a(在GF(2^8)中\\-a等于a本身,因为加法是异或运算)和一个乘法逆元a^{-1} 存在加法单位元(0)和乘法单位元(1),且对于域中的任意非零元素a,都存在一个加法逆元−a(在GF(28)中−a等于a本身,因为加法是异或运算)和一个乘法逆元a−1。
二、元素表示
在 G F ( 2 8 ) 域中,元素可以有两种主要表示方式 在GF(2^8)域中,元素可以有两种主要表示方式 在GF(28)域中,元素可以有两种主要表示方式:
- 整数表示:元素可以表示为0到255之间的整数。
- 二进制表示:元素也可以表示为8位二进制数,例如00000000(表示0)、00000001(表示1)、11111111(表示255)等。这些二进制数也可以看作是在某个n次不可约多项式(模多项式)下定义的二进制多项式。
三、运算规则
加法: 在 G F ( 2 8 ) 域中,加法通常定义为异或运算( X O R )。异或运算满足交换律和结合律,且对于任意元素 a ,都有 a + 0 = a 和 a + a = 0 (即 a 的加法逆元是 a 本身) 在GF(2^8)域中,加法通常定义为异或运算(XOR)。异或运算满足交换律和结合律,且对于任意元素a,都有a+0=a和a+a=0(即a的加法逆元是a本身) 在GF(28)域中,加法通常定义为异或运算(XOR)。异或运算满足交换律和结合律,且对于任意元素a,都有a+0=a和a+a=0(即a的加法逆元是a本身)。
乘法: 乘法运算则较为复杂,通常涉及模多项式运算。在 G F ( 2 8 ) 中,选择一个 8 次不可约多项式作为模多项式(如 x 8 + x 4 + x 3 + x + 1 ) 乘法运算则较为复杂,通常涉及模多项式运算。在GF(2^8)中,选择一个8次不可约多项式作为模多项式(如x^8+x^4+x^3+x+1) 乘法运算则较为复杂,通常涉及模多项式运算。在GF(28)中,选择一个8次不可约多项式作为模多项式(如x8+x4+x3+x+1),所有乘法运算都在该多项式下进行。乘法运算可以通过移位和异或操作来实现,具体规则如下:
- 当乘数为2的幂次时(如2、4、8等),可以通过左移操作来实现乘法。但需要注意的是,左移时可能会超出8位二进制数的范围,因此需要在左移后将超出部分与模多项式进行异或操作,以保证结果仍在 G F ( 2 8 ) GF(2^8) GF(28)域内。
- 对于一般的乘法运算,可以采用多项式乘法的方法,并将结果对模多项式进行取模操作。但在实际应用中,为了提高运算效率,通常会采用查表法或预计算等方法来优化乘法运算。
四、应用领域
G F ( 2 8 ) GF(2^8) GF(28)域在多个领域都有重要的应用:
- 密码学: 在加密算法中, G F ( 2 8 ) 域被用于限制数字的范围和提高算法的安全性。例如, A E S 加密算法中的列混淆步骤就使用了 G F ( 2 8 ) 域上的乘法运算 在加密算法中,GF(2^8)域被用于限制数字的范围和提高算法的安全性。例如,AES加密算法中的列混淆步骤就使用了GF(2^8)域上的乘法运算 在加密算法中,GF(28)域被用于限制数字的范围和提高算法的安全性。例如,AES加密算法中的列混淆步骤就使用了GF(28)域上的乘法运算。
- 编码理论: G F ( 2 8 ) 域是构建纠错码(如 B C H 码、 R S 码)的重要基础。通过 G F ( 2 8 ) 域上的多项式运算,可以实现数据的冗余编码和高效纠错 GF(2^8)域是构建纠错码(如BCH码、RS码)的重要基础。通过GF(2^8)域上的多项式运算,可以实现数据的冗余编码和高效纠错 GF(28)域是构建纠错码(如BCH码、RS码)的重要基础。通过GF(28)域上的多项式运算,可以实现数据的冗余编码和高效纠错。
- 数字信号处理: 在数字信号处理中, G F ( 2 8 ) 域可以用于设计滤波器、实现快速傅里叶变换等 在数字信号处理中,GF(2^8)域可以用于设计滤波器、实现快速傅里叶变换等 在数字信号处理中,GF(28)域可以用于设计滤波器、实现快速傅里叶变换等。
- 计算机科学: 在计算机科学中, G F ( 2 8 ) 域被用于设计算法和数据结构等。例如,在有限域上的乘法运算可以用于实现某些类型的哈希函数和随机数生成器 在计算机科学中,GF(2^8)域被用于设计算法和数据结构等。例如,在有限域上的乘法运算可以用于实现某些类型的哈希函数和随机数生成器 在计算机科学中,GF(28)域被用于设计算法和数据结构等。例如,在有限域上的乘法运算可以用于实现某些类型的哈希函数和随机数生成器。
综上所述, G F ( 2 8 ) GF(2^8) GF(28)域是一种具有特殊性质和运算规则的有限代数结构,在数学、密码学、编码理论、计算机科学等多个领域都有广泛的应用。
参考文献
1、矩阵,百度百科
2、代数余子式,百度百科
3、特征向量,百度百科
4、《密码学原理与实践(第三版)》
5、矩阵变换,百度百科
6、伴随矩阵,百度百科
7、文心一言
