哈希表

点赞👍👍收藏🌟🌟关注💖💖
你的支持是对我最大的鼓励,我们一起努力吧!😃😃
1.哈希表简介
哈希表是什么?
存储数据的容器
有啥用?
“快速” 查找某个元素。 时间复杂度O(1)
什么时候用哈希表?
频繁的查找某一个数的时候。
频繁查找某一个数的时候,我们还要想到一个二分查找也可以快速查找某一个元素,但是二分因为有些局限,具有二段性才可以用二分,它也比较快,时间复杂度O(logn)。而且能用二分我们尽量用二分,因为哈希表虽然非常快,但是它空间复杂度是O(n)。
怎么用哈希表?
- 容器(哈希表)
- 用数组模拟简易哈希表
什么时候会想到用数组模拟简易哈希表,比如说:
- 关注字符串中的 “字符”
其中key就是index,value就是nums[index],字符的ascll值当作index,nums[index]就是我们需要的值。非常快。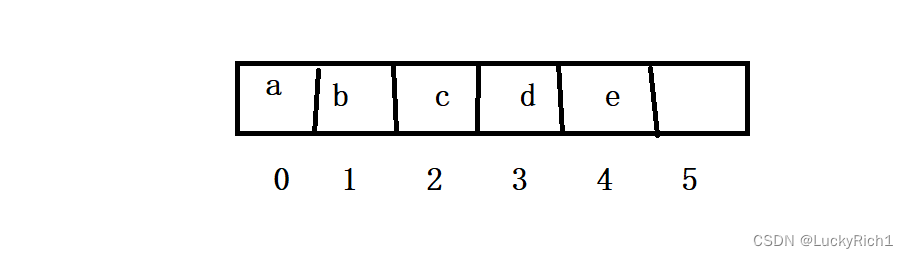
2. 数据范围很小的时候
int 1~10^7, 最好不要有负数, - 10^3 ~ 10^3
2.两数之和
题目链接:1. 两数之和
题目分析:

有且仅有一组答案,可以按任意顺序返回。数组中同一个元素在答案里不能重复出现。比如示例2 不能选两个3。
算法原理:
解法一:暴力求解
两层for循环把所有情况都找到,挑选符合条件的。
以前我们是固定一个数,然后往后找。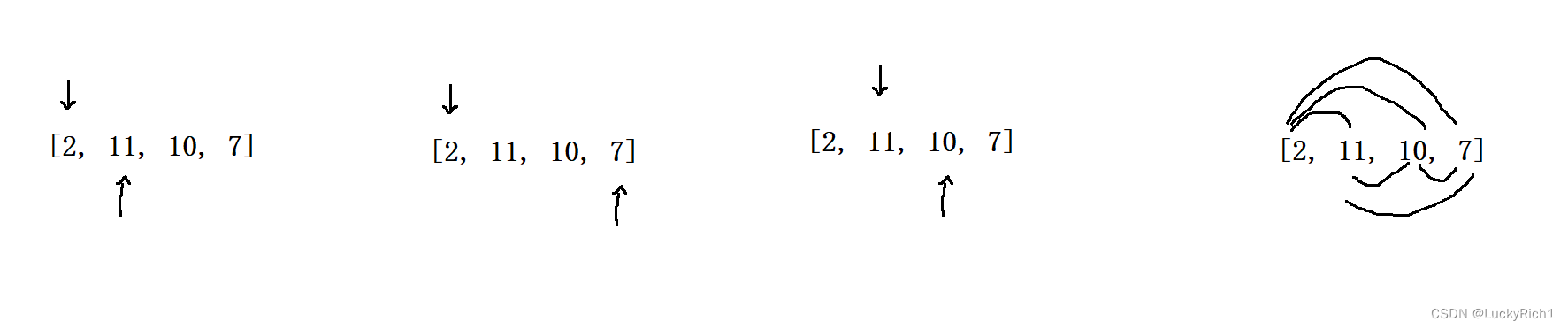
但是我们还有一种暴力方法,固定一个数,往前找
- 先固定其中一个数
- 依次与该数之前的数相加
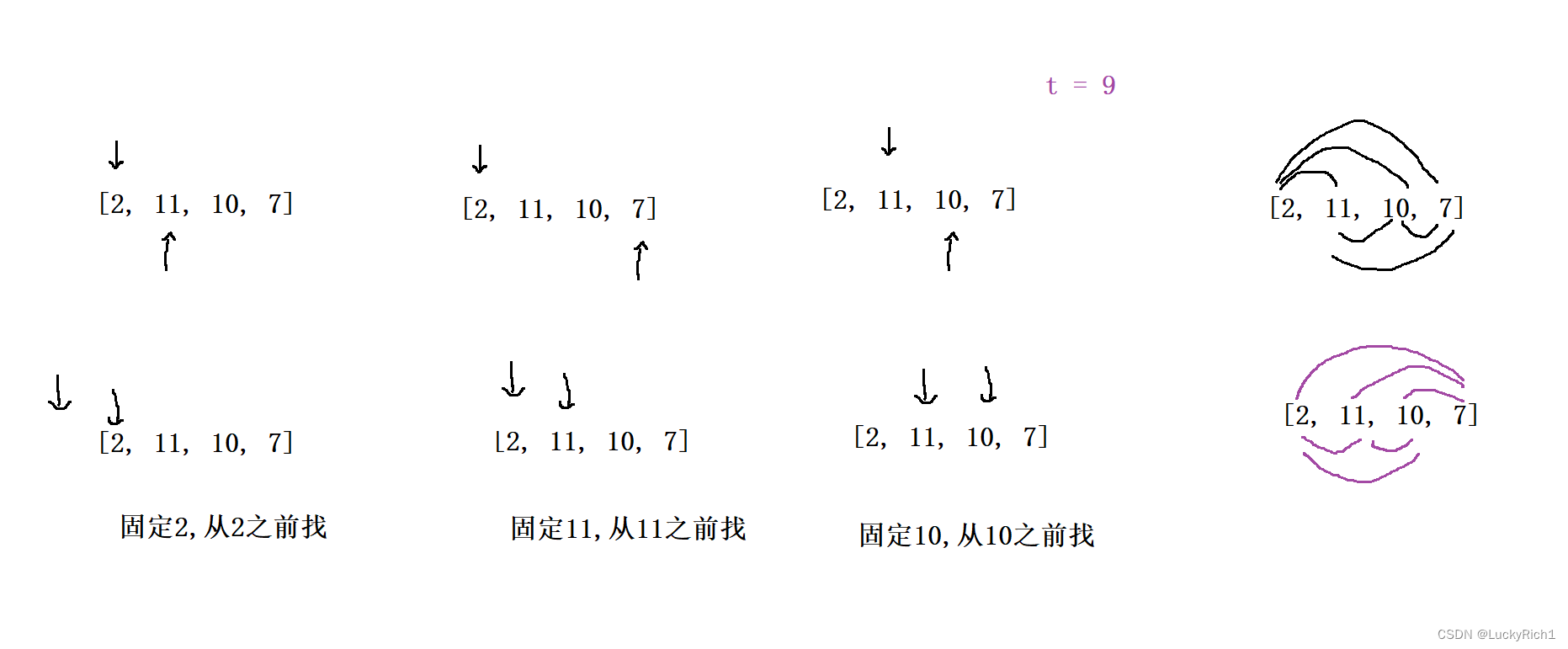
同样也能把所有情况都找完,并且少了判断边界情况。
解法二:利用哈希表做优化
我们先看为什么暴力枚举过程这么慢。慢就慢在当固定一个数的时候,比如说11,我们想在它的前面找到一个 target - nums[i] 的数 如 9 - 11 = - 2,我们暴力策略就是从11之前依次遍历找这个-2。那此时我如果当固定一个数的时候就把它之前的是插入到hash表中,然后在hash表中就可以用O(1)的时间复杂度来找这个-2。之前暴力解法O(N^2),利用哈希表做优化之后时间复杂度降到O(N)。不过我们空间复杂度是O(N)的。
具体如何操作可以和刚才的固定一个数往前找完美结合起来。当固定一个数的时候,就去hash表中找 target - nums[i] 的数在不在hash表。有就找到了返回对应两个数的下标即可,所有hash<nums[i] , i> 前面存值后面存对应的下标。如果没找到就把这个数加入到hash表中。
接下来扩展一下,为什么之前固定数,往后走不太好用呢?
首先要将所有的数,先加入到hash表中,然后才能固定一个数,在去hash找 target - nums[i] 的数在不在hash表。注意我们这道题有个求于数组中同一个数不能出现两次,如果target = 6,但是数组中有一个3, 你固定3然后在去hash表中找,找到的还是这个3,这是不对的。因为必须要加个if判断一下,当两个数相等时是不对的。而固定一个数往前找,是不会出现这种情况的。我们是先去找,。没找到在把这个数加入到hash表中。
class Solution { public: vector<int> twoSum(vector<int>& nums, int target) { // 1.暴力求解 // for(int i = 0; i < nums.size(); ++i) // for(int j = i - 1; j >= 0; --j) // if(nums[i] + nums[j] == target) // return {i,j}; // return {-1,-1}; // 2.利用哈希表优化 int n = nums.size(); unordered_map<int,int> mp(n); for(int i = 0; i < n; ++i) { int n = target - nums[i]; if(mp.find(n) != mp.end()) return {i,mp[n]}; else mp[nums[i]] = i; } return {-1,-1}; } }; 3.面试题 01.02. 判定是否互为字符重排
题目描述:

算法原理:
可以把 “abc” 全排列都找到,每找到一个就比较一下。全排列怎么搞,在递归专题哪里有。但是这样时间复杂度太高了。
解法一:利用哈希表
可以用两个hash表记录两个字符串中每个字符出现的次数,最后在比较一下两个hash表是否相等就行了。 我们可以用数组模拟hash表。
优化一下:只使用一个hash表。
将s1字符串中字符出现次数放到hash表,然后取出s2字符串中每个字符,对hash表字符对应位置进行减减操作。如果出现<0,说明就不是字符重排。还有当s1和s2字符串长度不相等也不是字符重排。
class Solution { public: bool CheckPermutation(string s1, string s2) { if(s1.size() != s2.size()) return false; int hash[26] = {0}; for(auto& ch : s1) hash[ch - 'a']++; for(auto& ch : s2) if(--hash[ch - 'a'] == -1) return false; return true; } }; 4.存在重复元素
题目链接:217. 存在重复元素
题目描述:
算法原理:
解法:哈希表
这道题和最开始那道题的解题思路是一样的。前面那道题固定一个数往前找找有没有出现 target - nums[i] 的数,遍历找太麻烦了,因此来一个hash表快速查找前面有没有出现target - nums[i] 的数。 这道题固定一个数往前找找有没有出现和我一样的数,也是利用哈希表快速查找。
class Solution { public: bool containsDuplicate(vector<int>& nums) { unordered_set<int> hash; for(auto& x : nums) if(hash.count(x)) return true; else hash.insert(x); return false; } }; 5.存在重复元素 II
题目链接:219. 存在重复元素 II
题目分析:
上一道题仅是找到重复元素即可,但是这道题不仅要是重复元素,而且重复元素的下标必须满足 abs(i - j) <= k
算法原理:
解法:哈希
还是固定一个数,往前找,看看有没有出现重复元素,可以用hash快速查找,不过这道题有点不一样的就是,我们还需要知道元素对应的下标,因此可以使用unordered_map<int,int>,记录nums[i] 对应的下标。这里有一个细节问题,两个相同元素下标之差要小于等于k,unordered_map不允许插入相同的元素,value会覆盖。但是这正好满足我们abs(i - j) <= k,因为我们就是想要找距离小的。

class Solution { public: bool containsNearbyDuplicate(vector<int>& nums, int k) { unordered_map<int,int> hash; for(int i = 0; i < nums.size(); ++i) if(hash.count(nums[i]) && abs(hash[nums[i]] - i) <= k) return true; else hash[nums[i]] = i; return false; } }; 6.字母异位词分组
题目链接:49. 字母异位词分组
题目分析:
字母异位词就是,将原有字符串的字符重新排序得到的新的字符串。这道题要求将属于同一个字母异位词放在一块。

算法原理:
解法:哈希表
这道题我们要解决的有两个问题:
- 如何判断两个字符串是字母异位词
- 如何分组
如何判断两个字符串是字母异位词,我们可以用之前的思路,弄一个hash表统计每个字符出现的次数。不过代码写着有点麻烦。这里我们可以将字符串按照ascll码 排序!如果是相同的字母异位词拍完序后是一样的。
如何分组,分组是将相同的字母异位词添加到属于自己的数组中。因此这里我们可以来一个unordered_map<string,vector>,string 排序后的字符串,vector 是属于相同字母异位词的数组。

class Solution { public: vector<vector<string>> groupAnagrams(vector<string>& strs) { vector<vector<string>> ret; unordered_map<string, vector<string>> hash; // 1.把所有字母异位词分组 for(auto& s : strs) { string str = s; sort(str.begin(),str.end()); hash[str].push_back(s); } // 2.结果提取出来 // for(auto& str : hash) // { // ret.push_back(str.second); // } //提取pair对象, first放x里, second放y里 for(auto& [x,y] : hash) { ret.push_back(y); } return ret; } }; 