【算法/学习】单调队列&&单调栈

✨                                                       海压竹枝低复举，风吹山角晦还明      🌏 

📃个人主页：island1314

🔥个人专栏：算法学习

🚀 欢迎关注：👍点赞 👂🏽留言 😍收藏  💞 💞 💞

---

单调队列&&单调栈目录

一、单调队列

基本概念

​编辑

滑动窗口

方法1：（数组实现）

方法2：（双端队列）

区间最值

方法1：（数组实现）

方法2：（双端队列）

二、单调栈

基本概念

三、总结

---

一、单调队列

   用来维护一段区间内的最大值或最小值，例如滑动窗口、区间最值等问题。

基本概念

单调队列是一种存储数据的队列，其中元素的顺序是单调递增或单调递减的。在算法竞赛中，我们一般使用两个单调队列，一个维护单调递增序列，另一个维护单调递减序列。单调队列是一个双端队列。

代码如下：

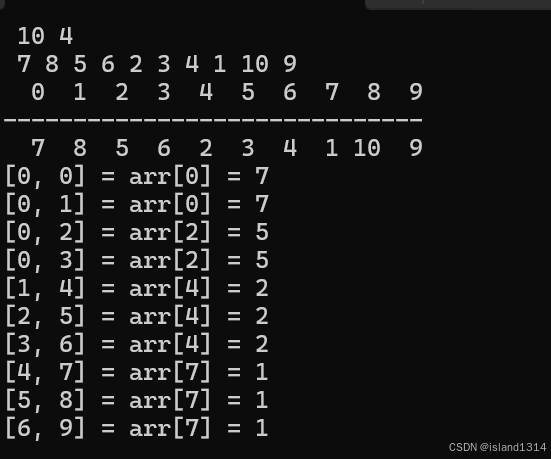
#include <iostream> #include <deque> #include <vector> #include <algorithm> using namespace std;  void output(vector<int>& arr) { 	int n = arr.size(), len = 0; 	for (int i = 0; i < n; i++) len += printf("%3d", i); 	cout << "\n"; 	 	for (int i = 0; i < len; i++)printf("-"); 	cout << "\n"; 	 	for (int i = 0; i < n; i++) len += printf("%3d", arr[i]); 	cout << "\n"; }  int main(){ 	int n, k; 	cin >> n >> k; 	vector<int> arr; 	deque<int> q; 	for (int i = 0, a; i < n; i++) { 		cin >> a; 		arr.push_back(a); 	} 	output(arr); 	for (int i = 0; i < n; i++) { 		while (!q.empty() && arr[q.back()] > arr[i])q.pop_back(); 		q.push_back(i); //压入下标 		if (i - q.front() == k) q.pop_front(); //弹出队头 		printf("[%d, %d] = arr[%d] = %d \n", 			max(i - k + 1, 0), i, 			q.front(),arr[q.front()]); 	} }

滑动窗口

154. 滑动窗口 - AcWing题库

滑动窗口是一类问题，需要在一个长度为n的序列中，找到所有长度为k的连续子序列中的最大值或最小值。使用单调队列可以在O(n)的时间复杂度内解决该问题。

具体做法如下：

（1）将前k个元素插入单调队列中，并记录队列的最大值或最小值。
（2）从第k+1个元素开始，每次将一个新的元素插入单调队列中。
（3）插入时，先将队列中所有小于等于该元素的队尾元素出队，保证队列中的元素单调递减。
（4）将该元素插入队尾，并记录队列的最大值或最小值。
（5）将长度为k的子序列的最大值或最小值输出即可。

方法1：（数组实现）

#include <iostream> using namespace std;  const int N = 1e6 + 10; int q[N], a[N]; //数组q用来存下标 int main() { 	int n, k; 	cin >> n >> k; 	for (int i = 0; i < n; i++) cin >> a[i];  	//找滑动窗口最小值 	int hh = 0, tt = -1; 	for (int i = 0; i < n; i++) { 		if (i - q[hh] == k) hh++; //队头弹出元素 		while (hh <= tt && a[q[tt]] > a[i]) tt--; //队尾弹出元素 		q[++tt] = i; //压入下标 		if (i - k + 1 >= 0)printf("%d ", a[q[hh]]); 	} 	printf("\n"); 	//找滑动窗口最大值 	hh = 0, tt = -1; 	for (int i = 0; i < n; i++) { 		if (i - q[hh] == k) hh++; //队头弹出元素 		while (hh <= tt && a[q[tt]] < a[i]) tt--; //队尾弹出元素 		q[++tt] = i; //压入下标 		if (i - k + 1 >= 0)printf("%d ", a[q[hh]]); 	} 	return 0; } 

方法2：（双端队列）

#include <iostream> #include <deque> #include <vector> using namespace std;  int main() { 	int n, k; 	cin >> n >> k; 	vector<int> arr(n); 	deque<int> q; 	for (int i = 0; i < n; i++)cin >> arr[i]; 	for (int i = 0; i < n; i++) { 		if (i - q.front() == k) q.pop_front(); 		while (!q.empty() && arr[q.back()] > arr[i])q.pop_back(); 		q.push_back(i); 		if (i - k + 1 >= 0) cout << arr[q.front()] << " "; 	} 	cout << endl;  	q.clear(); 	for (int i = 0; i < n; i++) { 		if (i - q.front() == k) q.pop_front(); 		while (!q.empty() && arr[q.back()] < arr[i])q.pop_back(); 		q.push_back(i); 		if (i - k + 1 >=0) cout << arr[q.front()] << " "; 	} 	return 0; } 

区间最值

135. 最大子序和 - AcWing题库

需要在一个长度为n的序列中，找到所有长度为k的子序列中的最大值或最小值。使用单调队列可以在O(n)的时间复杂度内解决该问题。

其实现方法与上面类似，但是需要注意：

• 区间最值问题是在不限制子序列连续性的情况下，找到子序列中的最大值或最小值。
• 而滑动窗口问题则是在限制子序列必须连续的情况下，找到所有长度为k的子序列中的最大值或最小值。

方法1：（数组实现）

#include <iostream> #include <algorithm> #include <cstring> using namespace std;  typedef long long LL;  const int N = 1e6 + 10; int q[N]; LL s[N]; int main() { 	int n, m; 	cin >> n >> m; 	//处理为前缀和序列 	for (int i = 1; i <= n; i++) { 		cin >> s[i]; 		s[i] += s[i - 1]; 	} 	LL res = -1e10; 	int hh = 0, tt = 0; 	for (int i = 1; i <= n; i++) { 		if (i - q[hh] > m) hh++; 		res = max(res, s[i] - s[q[hh]]); 		while (hh <= tt && s[q[tt]] >= s[i]) tt--; 		 		q[++tt] = i; 	} 	cout << res << "\n"; 	return 0; } 

方法2：（双端队列）

#include <iostream> #include <algorithm> #include <cstring> #include <deque> #include <vector> #include <algorithm> using namespace std; typedef long long LL;  int main() { 	int n, m; 	cin >> n >> m; 	//处理前缀和 	vector<LL> s(n + 1); 	s.push_back(0); 	deque<LL> q; 	for (int i = 1; i <= n; i++) { 		cin >> s[i]; 		s[i] += s[i - 1]; 	} 	q.push_back(0); 	LL res = -1e6; 	for (int i = 1; i <= n; i++) { 		if (i - q.front() > m) q.pop_front(); 		res = max(res, s[i] - s[q.front()]); 		while (!q.empty() && s[q.back()] >= s[i]) q.pop_back(); 		q.push_back(i); 	} 	cout << res << "\n"; 	return 0; }  

二、单调栈

基本概念

单调栈实际上就是栈，只是利用了一些巧妙的逻辑，使得每次新元素入栈后，栈内的元素都保持有序（单调递增或单调递减），即从队首不弹出元素的单调队列就是单调栈。

作用：用于找最近小于关系（单调递增）和最近大于关系（单调递减）

代码如下：

#include <iostream> #include <stack> #include <vector> #include <algorithm> using namespace std;  void output(vector<int>& arr) { 	int n = arr.size(), len = 0; 	for (int i = 0; i < n; i++) len += printf("%3d", i); 	cout << "\n"; 	 	for (int i = 0; i < len; i++)printf("-"); 	cout << "\n"; 	 	for (int i = 0; i < n; i++) len += printf("%3d", arr[i]); 	cout << "\n"; }  int main(){ 	int n; 	cin >> n; 	vector<int> arr; 	arr.push_back(-1); //假如极小值为-1 	stack<int> s; 	for (int i = 0, a; i < n; i++) { 		cin >> a; 		arr.push_back(a); 	} 	arr.push_back(-1); //假如极小值为-1 	vector<int> l(arr.size() + 1), r(arr.size() + 1); 	output(arr);  	//右侧 	for (int i = 0;  i < arr.size(); i++) { 		while (!s.empty() && arr[s.top()] > arr[i]) { 			r[s.top()] = i; 			s.pop(); 		} 		s.push(i); 	}  	//左侧 (倒着扫描) 	while (!s.empty()) s.pop(); 	for (int i = arr.size() - 1; i >= 0; i--) { 		while (!s.empty() && arr[s.top()] > arr[i]) { 			l[s.top()] = i; 			s.pop(); 		} 		s.push(i); 	}  	for (int i = 1; i <= n; i++) { 		printf("arr[%d] = %d, right : arr[%d] = %d, left : arr[%d] = %d\n", 			i, arr[i], 			r[i], arr[r[i]], 			l[i], arr[l[i]]); 	} 	return 0; }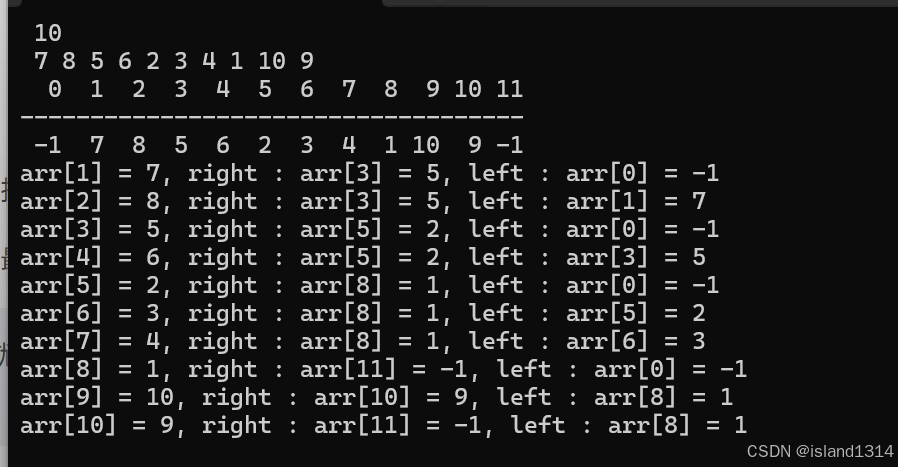 

数组实现单调栈：

830. 单调栈

#include <iostream> using namespace std; const int N = 10010;  int stk[N], tt ; int main() { 	int n; 	cin >> n; 	while(n--) 	{ 	    int x; 	    cin>>x; 	    while(tt&&stk[tt]>=x) tt--; 	    if(tt==0) printf("-1 "); 	    else printf("%d ",stk[tt]); 	    stk[++tt]=x; 	} 	return 0; }

三、总结

单调队列：擅长维护区间【最大/最小】值，最小值对应单调递增队列

单调栈：擅长维护最近【大于/小于】关系，

从左侧先入栈就是维护左侧最近关系

从右侧先入栈，就是维护右侧最近关系。