题目主体需要关注的地方attention!!!
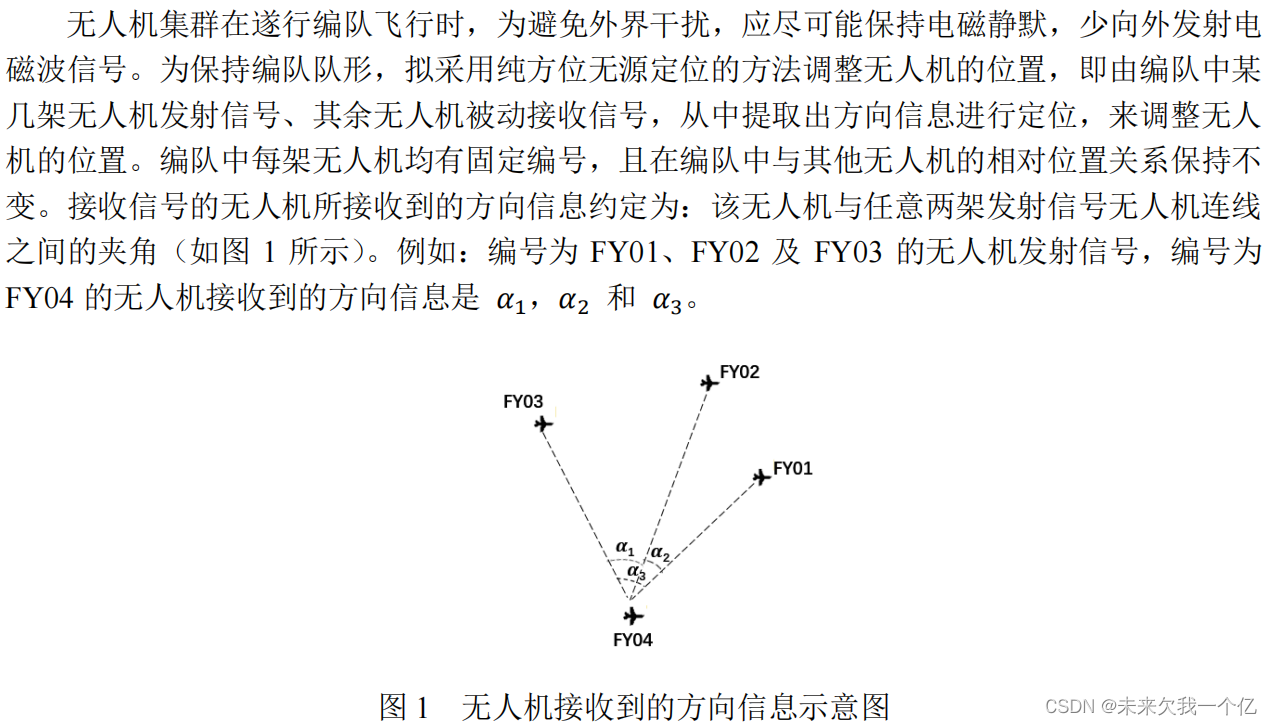
1.无人机集群在遂行编队飞行时,为避免外界干扰,应尽可能保持电磁静默,少向外发射电磁波信号。
2.接收信号的无人机所接收到的方向信息约定为:该无人机与任意两架发射信号无人机连线之间的夹角
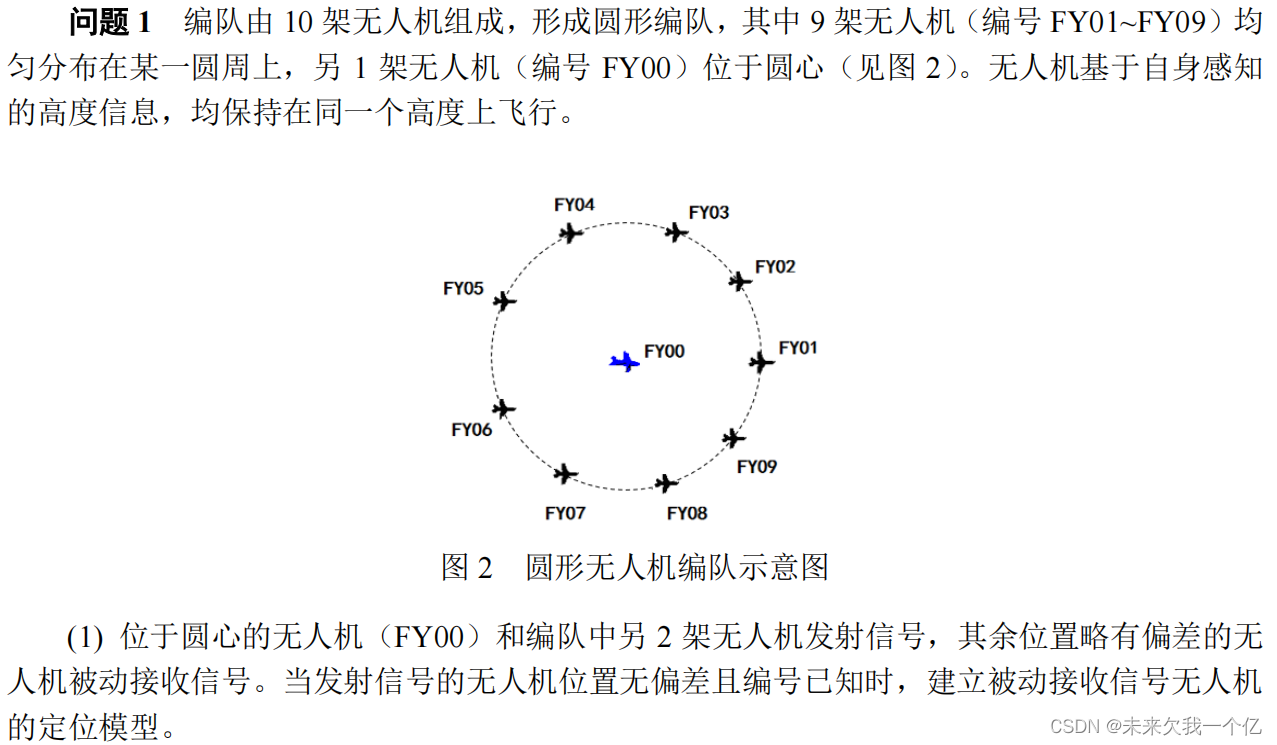
问题1.1 模型的建立与求解
根据三架无人机相对位置信息进行讨论
结合正弦定理,确定定位模型,采用遍历算法,固定一架发射信号无人机,遍历另外两架无人机的相对位置关系,求解每种情况下所有位置上被动接收无人机的实际坐标,输出图解结果。
怎么分类?
建立极坐标
以圆心无人机 为极坐标原点,两架发射信号的无人机极坐标分别记作
为极坐标原点,两架发射信号的无人机极坐标分别记作 ,
, (下图中的黑色弧线和红色弧线),固定
(下图中的黑色弧线和红色弧线),固定 。位置略有偏差的无人机记为
。位置略有偏差的无人机记为 ,可以将位置关系分为三类:
,可以将位置关系分为三类:
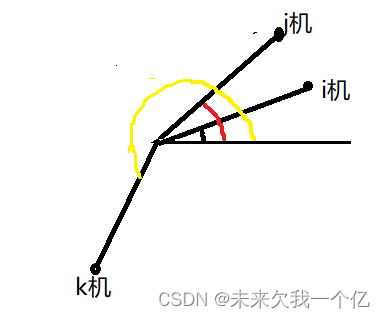
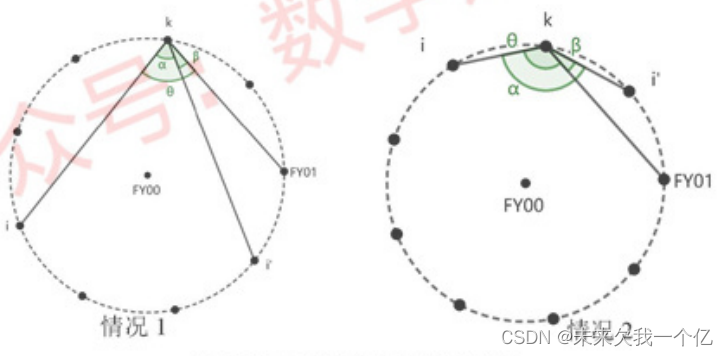
情况1.
分为三小类:
![]()

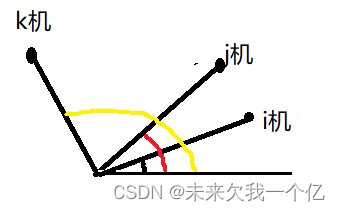
极坐标的求解过程:
记圆心为o, 表示∠oki,
表示∠oki, 表示∠okj,
表示∠okj, 表示接收的角度信号∠oki值存在的偏差,
表示接收的角度信号∠oki值存在的偏差, 表示接收的角度∠okj值存在的偏差。
表示接收的角度∠okj值存在的偏差。

由正弦定理可得

得到
 或
或
两个等式是等价的,根据 ,可以得到:
,可以得到:

![]()

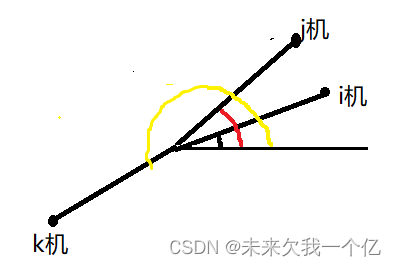
同理可得:
 或
或

![]()

同理可得

情况2.
同样分三小类
![]()

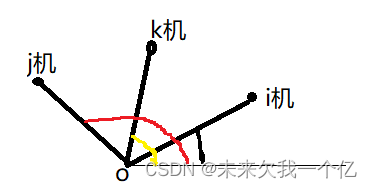
第一小类的模型:

![]()


第二小类的模型:

![]()

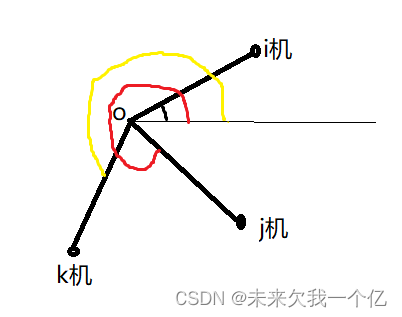
第三小类的模型:

情况 3.
此类情况与情况1具有几何对称性,通过旋转会发生重叠,属于同一种情况,在这里仅讨论情况1
可进行真实的仿真模拟,进一步说明结果。
问题1.2 模型的建立与求解

由1.1的方法一可以知道,对于被动接受信号的无人机的有效定位需要两架圆周上已知编号的无人机i,j发射的角度信息,以及自身的坐标信息和被动接受消息的无人机的相对位置的无偏角度。
问题二给出了FY00和FY01的具体位置,接收信号无人机k已经知道自身编号的情况下,可初步判断为另需一架无人机发射信号,即可对自身实现有效定位。
假设被动接收信号的无人机知道自己的具体编号,即k=2,3,...,8,9即自身编号与FY01相对位置已知,基于此,再引入一架未知编号的发射信号的无人机记为FY0i
第一步,首先确定FY0k与FY0i的相对位置关系
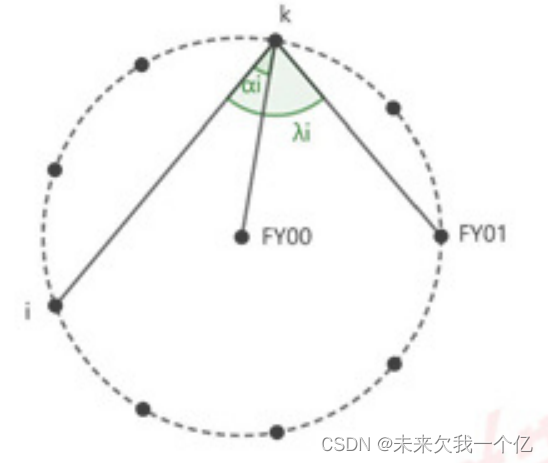
用n来表示无人机i,无人机k之间间隔的无人机数量。通过n即可初步判断无人机i,k的相对位置关系如下:

由发射过来的 ,我们知道了接受信号的无人机与发射信号的无人机(但并不知道自己编号)之间有几架无人机,但我们不确定是在接受信号的无人机左侧还是右侧,因此进行下面这一步:
,我们知道了接受信号的无人机与发射信号的无人机(但并不知道自己编号)之间有几架无人机,但我们不确定是在接受信号的无人机左侧还是右侧,因此进行下面这一步:
第二步,锁定FY0i的相对位置坐标
当k=2,3,4,5时

当k=6,7,8,9时

当n与k之间的关系取等号时,说明无人机i与无人机FY01关于无人机j对称,无人机i的相对位置坐标随即确定。
假定无人机i始终偏离FY01,无人机i'始终靠近无人机FY01,则有角度大小关系如下
当k=2,3,4,5时

当k=6,7,8,9时

即通过判断
 (位于左侧)
(位于左侧)
或
 (位于右侧)
(位于右侧)
来进行进一步的确定,至此,第二步的建模也完成了。
问题1.3 模型的建立与求解
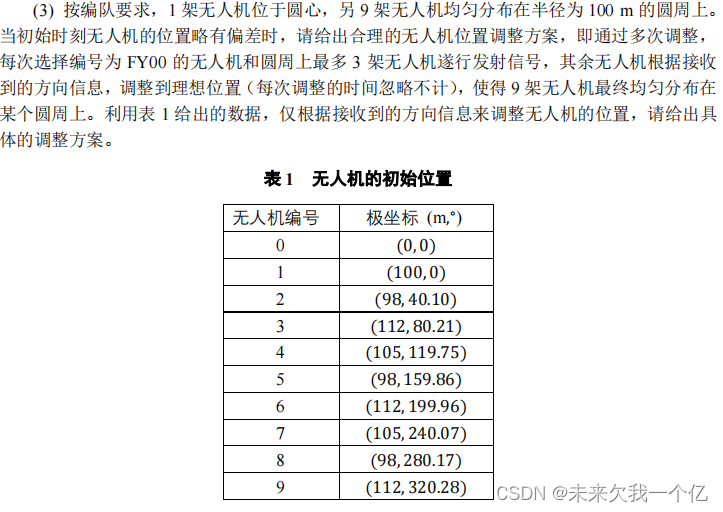
题中前面说分布在半径为100m ,是说的原本状态是大概分布在以半径为100 m的圆上,后面调整后是分布在某一圆周上,所以还是要看清题!!!
根据表格我们将本题调整到半径为98的圆周上。
步骤一利用问题一(1)的定位模型,调整同一圆周上的三架无人机的相对位置接近理想位置关系:
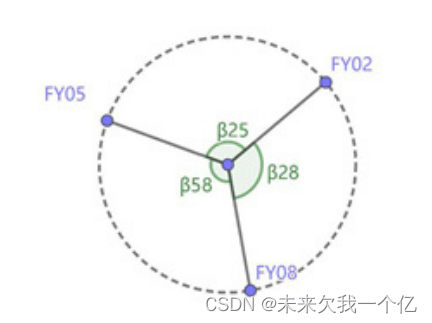
根据2、5、8位置的特殊性,本题中 ,可知
,可知
我们可以将FY02,FY08作为理想位置,FY05作为理想坐标。
就可以利用1.1中的第四个模型,得到




最终得到

调整后可通过式 反复迭代,使方案结果逼近无偏值。
反复迭代,使方案结果逼近无偏值。
步骤二以步骤一中三架无人机为参照系,利用问题一(1)的定位模型,调节余下无人机的角度坐标,使之接近理想相对位置,输出角度调节量 :
2,5,8之间均间隔两架无人机。可利用问题1.1中的模型再次求解。由于方法一致,在这里不作赘述。同样可得到调整角度。
步骤三同步骤二参照基准,建立几何关系模型,调节余下无人机的长度坐标。每一步骤都对应各自独立的调整模型,模型求解利用迭代算法进行。
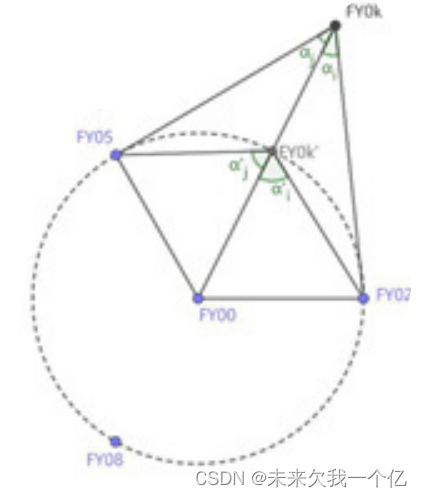



可通过仿真进一步说明。
问题2 模型的建立与求解
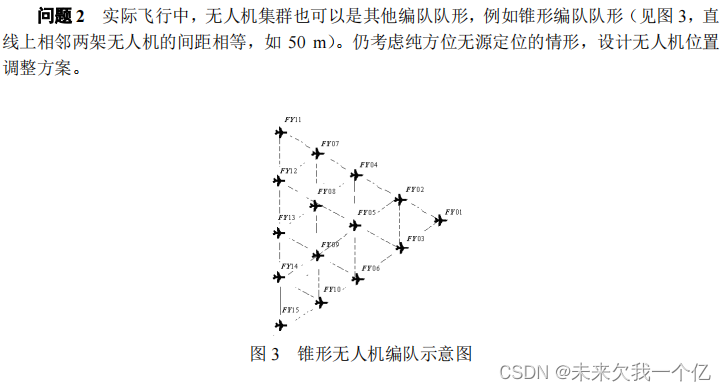
将锥形编队分解成多个同心圆的圆形编队,利用问题一(3)中给出的调节方案调整各圆周上无人机,针对特殊点通过共线无人机制定相应的调整方案。
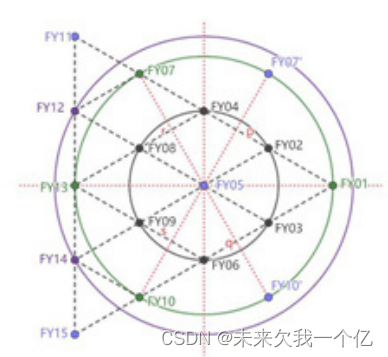
可以分为四组分别进行求解
1.FY02,FY03,FY04,FY06,FY08,FY09
2.FY01,FY07,FY10,FY13
3.FY12,FY14
4.FY11,FY15
前三组可利用问题1.3的调整方案FY11,FY15两架无人机位置调整利用接收到的随机两组共线无人机发射的信号角度信息来确定。
对于第四组角度坐标 可利用角度的平均确定。
可利用角度的平均确定。
长度坐标 根据正弦定理,根据角度坐标来确定。
根据正弦定理,根据角度坐标来确定。
