前言
在上一篇文章,我们学习了插入排序,选择排序以及交换排序中的冒泡排序,接下来我们继续学习交换排序、归并排序以及非比较排序。
1. 快速排序
快速排序是交换排序的一种,它的基本思想:任取待排序序列中的某元素作为基准值,按照该基准值将集合分割为两个子序列,左边的小于基准值,右边的大于基准值,如何左右子序列重复该过程,知道所有元素都排列到对应位置,每次排序后基准值所在的位置就是排好序后其所在的位置。
快速排序有四个版本,其中三个通过递归实现,一个通过非递归实现。
快速排序递归版本的框架:

分析:当left>right时肯定要停止,因为区间[left,right]间没有数据,当相等时也停止,因为只有一个数据,不用进行划分。
在继续划分的前提下,找到基准值,划分为两个区间,[left,key-1],[key+1,right]继续划分。
1.1 hoare版本的快速排序
思路:
1.创建左右指针用来确定基准值。
2. 从右到左找比基准值小的数据,从左到右找比基准值大的数据,将左右指针进行交换。

代码分析:
我们将最左边的数据设为基准值,在left<right 的前提下进行从右找小,从左找大的操作,当找到后进行交换的操作,交换的前提也是left<right,交换完之后将left++,right--。当遍历完数组后,将基准值和right进行交换,此时的right就是基准值。
left都<=right。
1.2 挖坑版
思路:设置左右指针,将最左边的位置设为坑位,将其数据作为基准值临时保存,从右到左找比基准值小的数据,填入坑,此时找到的位置为坑位,再从左到右找大于基准值的数据,找到了填入坑位,形成新坑。直到左指针大于右指针。最后将坑填为基准值。
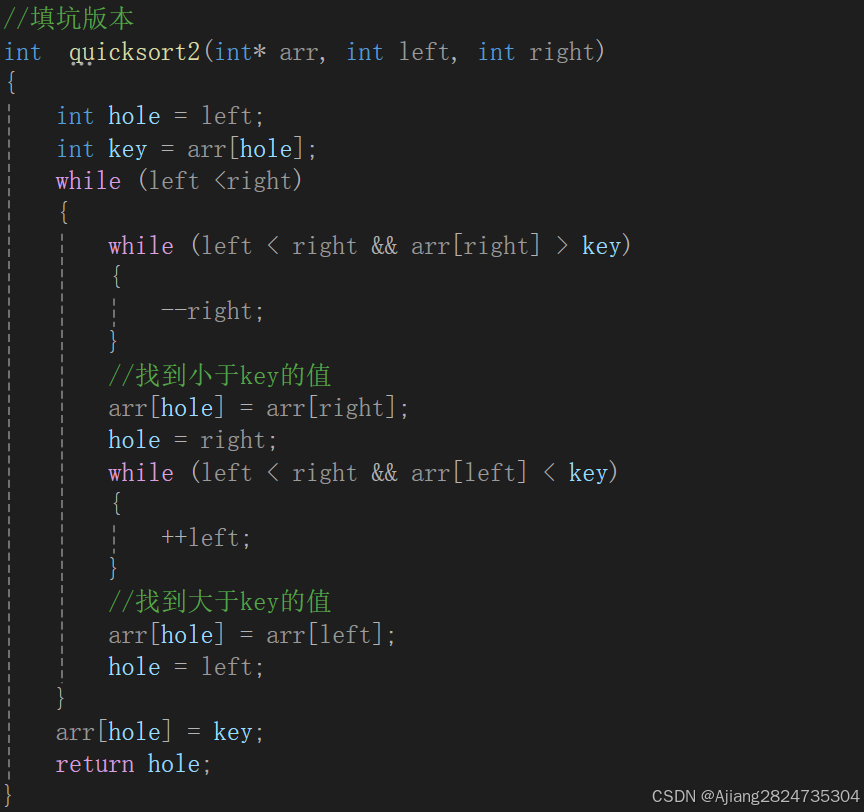
left都小于right。
1.3 lomuto版本
思路:将最左边数据设置为基准值,设置两个指针,一个cur用于遍历数组,找到小于基准值的就让prev指针++,然后将小与基准值的数据与prev位置的进行交换。最后将prev指针与基准值进行交换。
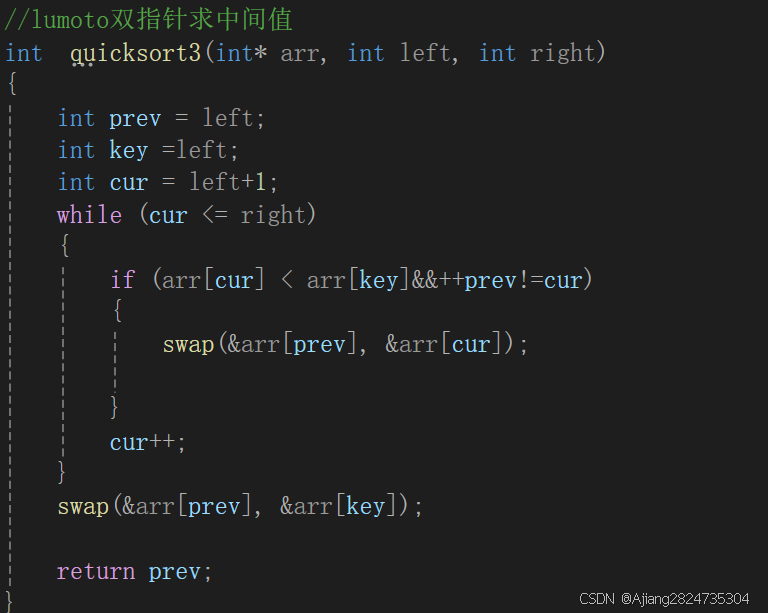
快速排序时间复杂度:O(nlogn)。
空间复杂度:O(logn)
1.4 非递归版本
非递归版本实现需要借助数据结构:栈
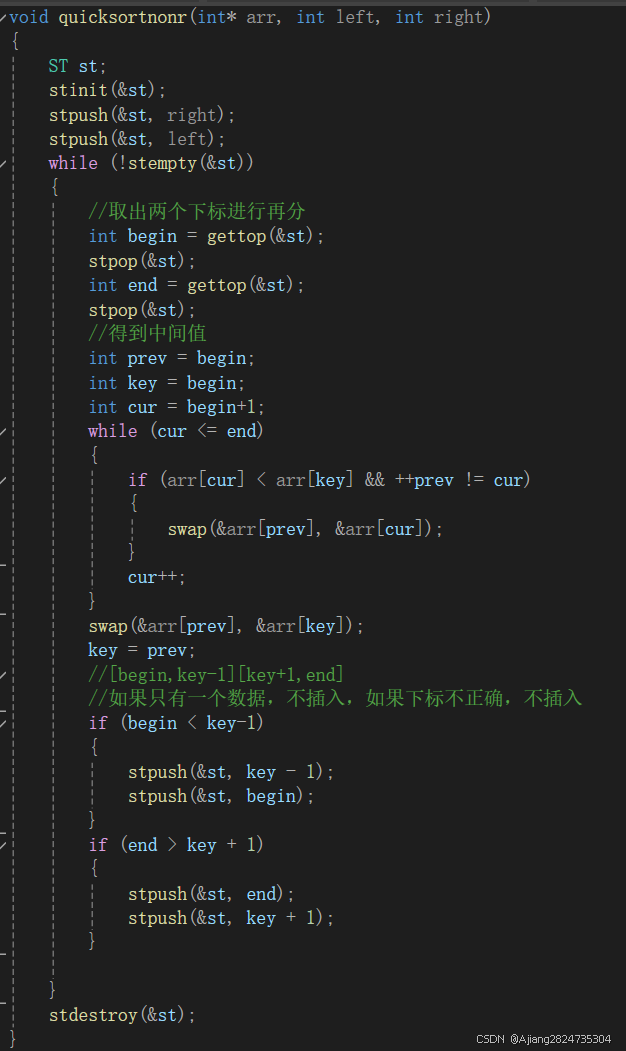
思路:向栈中插入最左边和最右边的,取出两个数据的下标,通过之前实现的方法找这个区间的基准值,找到基准值后,如果此时基准值右边的end>key+1或left<key-1,则这个区间里面还有数据,则将[left,key-1],[key+1,end]进行入栈操作,再依次进行取两个元素出栈,直到栈为空。
2. 归并排序
归并排序中的归并指的是递归和合并,即通过递归将数据集合分为一个一个的单独数据,然后通过合并数据依次将数据进行有序化。
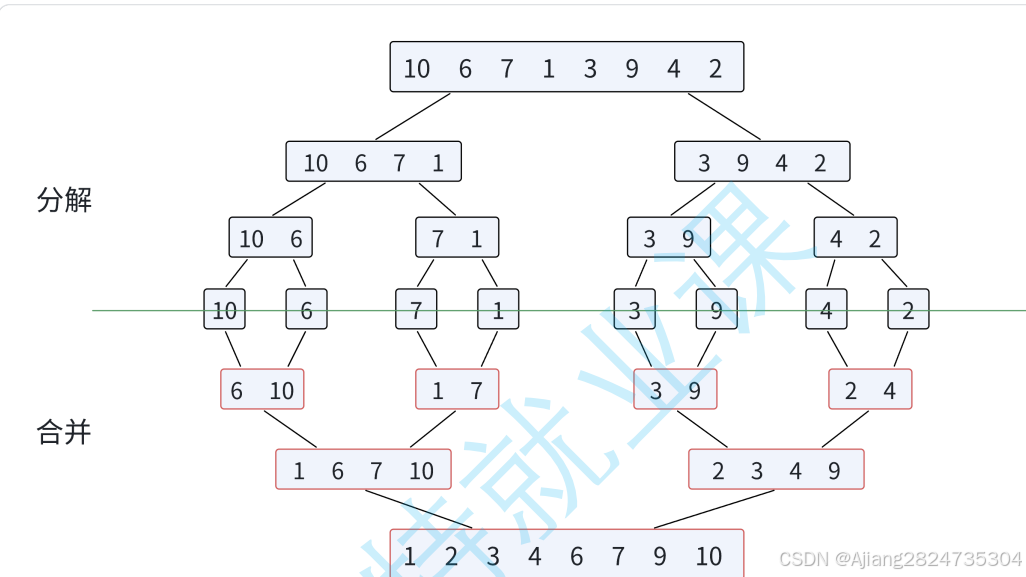
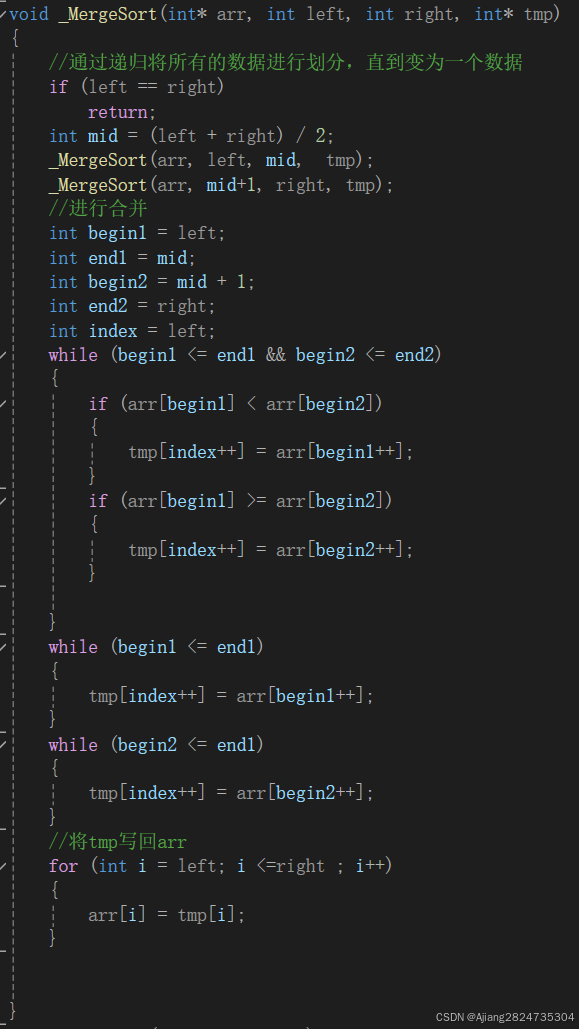
分为一个一个数据可以通过上面的递归进行。但不同的是,每个数据都要进行划分,所以区间为[left,key][key+1,right]。
合并的思路:创建一个临时的数组tmp,该数组大小为n,填入数组的时候通过判断大小,小的填入,当一个数组遍历完之后,剩下的依次填入tmp,当最终填完后将tmp覆盖到原数组里面。
3.非比较排序——计数排序
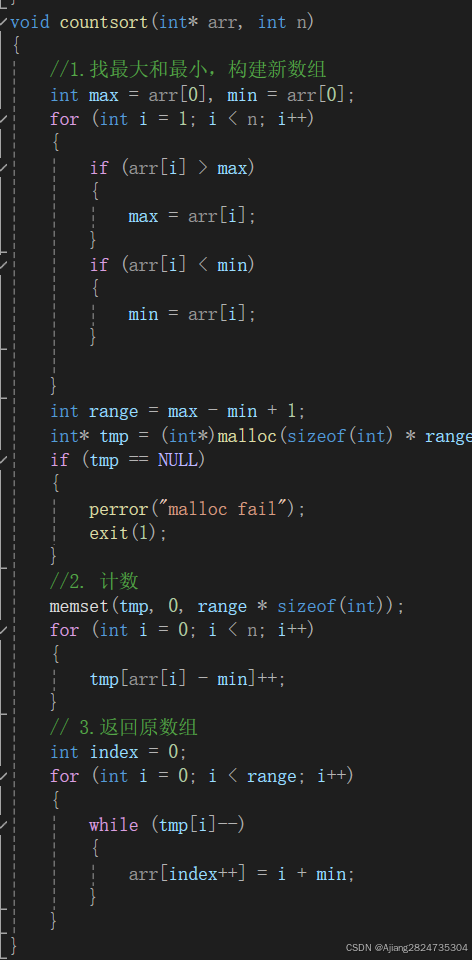
思路:遍历数组,将每个数据出现的次数记录,并找到最大值与最小值,开辟最大值-最小值+1个空间的临时数组并将其值全部变为0,临时数组的下标就是数据的值,而下标对应的数据就是出现次数。排序时遍历临时数组,将下标输入原数组。
为了更好的应用于负数以及跨度较大的数据,我们可以将临时数组的下标对应的值稍作修改,例如:遇到[100,102,101,101,105]这样的数据,我们可以将临时数组下标为0的位置对应为100,下标为1的位置对应为101,以此类推。
特点:计数排序在数据范围集中时效率很高,但应用范围及场景很有限。
时间复杂度:O(N+range)。
空间复杂度:O(range)。
稳定性:稳定。
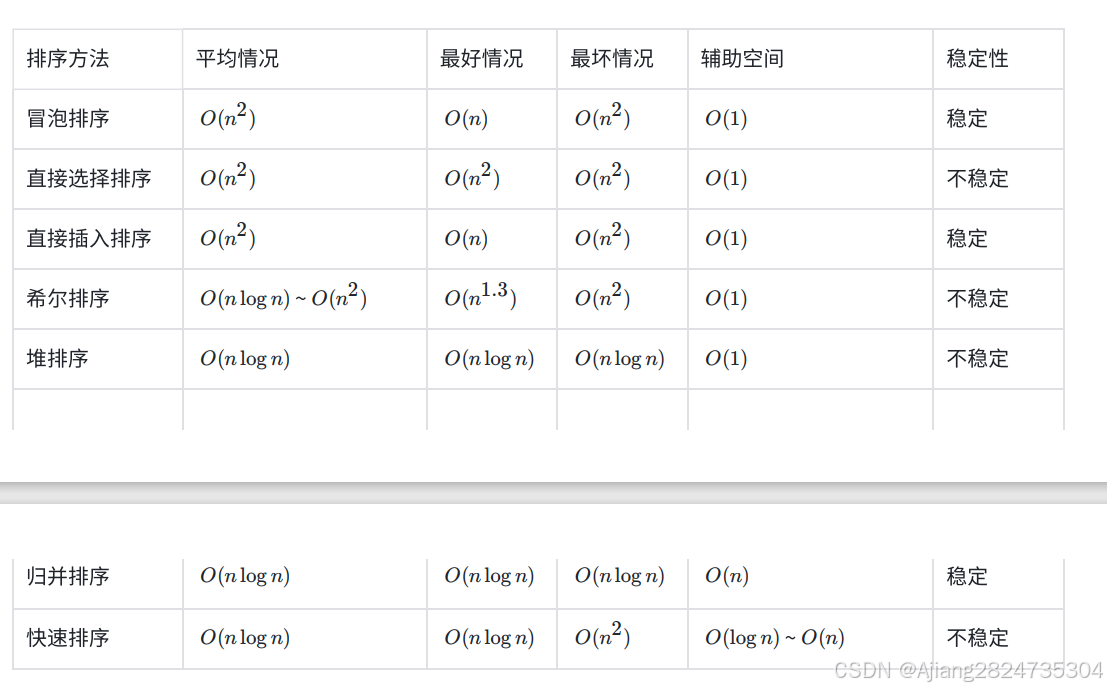
4. 排序算法的复杂度及稳定性
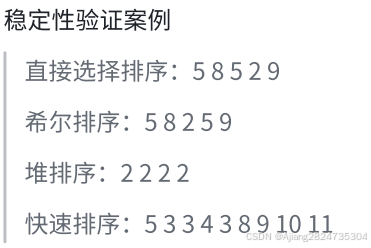
稳定性:待排序序列中多个相同关键字在经过排序后的相对次序不变,则称为稳定,否则不稳定。