目录

整数在内存中的存储
要介绍整数在内存中的存储就要先介绍整数的二进制表示形式。
整数的3种二进制表示形式
原码:直接将数值按照正负数的形式翻译成二进制得到的就是原码。 例如 5的二进制原码就是00000101;-5的二进制原码就是10000101。
反码:将原码符号位不变其余依次按位取反。 例如 5的二进制反码就是01111010;-5的二进制反码就是11111010。
补码:反码加1得到补码。 例如 5的二进制反码就是01111011;-5的二进制反码就是11111011
声明:在3中表示形式中第一位都是符号位,0表示正,1表示负。 对于整数来说,在内存中存储的就是补码。
浮点数在内存中的存储
根据国际标准IEEE(电气和电子工程协会)754,一个浮点数V可以表示为
例如:5.5写成二进制为101.1,相当于1.011*2^2。即S = 0, M = 1.011, E = 2。
-5.5写成二进制为-101.1,相当于(-1)^ 11.0112^2。即S = 1, M = 1.011, E = 2。
IEEE 754规定32位浮点数最高一位存储符号位S,接着8位储存指数E,剩下23位存储有效数字M。
IEEE 754规定64位浮点数最高一位存储符号位S,接着11位储存指数E,剩下52位存储有效数字M。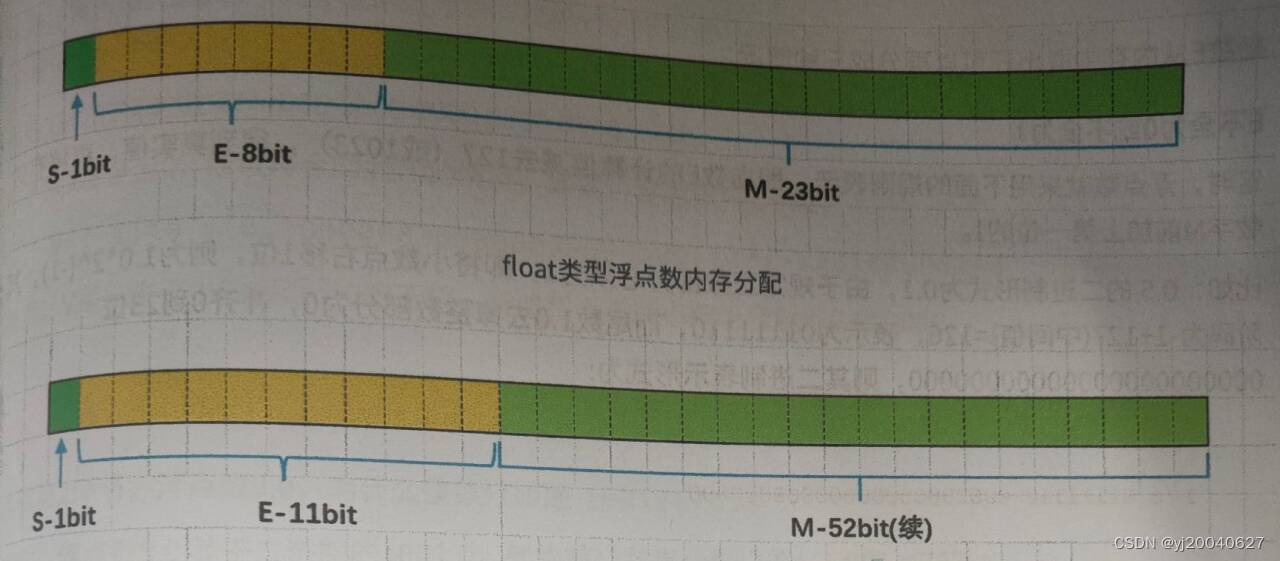
浮点数存储过程
S的存储没有什么好说的直接存储就行。
M的存储
像平时我们的10进制中的科学计数法类比过来就好理解了。M的范围是1~2,所以M永远是1.XXXX, 1永远有,所以存储进内存时1会舍去只保留小数点后的数,读取时再加回来。
E的存储
根据上面E的存储字节是8和11,所以范围是0~255 和 0 ~ 2047,但是如果是这样的话E只能是正数,但是科学计数法中E是可以为负数的。
因此IEEE 754规定了一个中间值来完成这个操作。分别是127和1023。
在将E存储进内存前会先加上中间数。E的取出因此也会不同。
E的取出3种情况
E的取出3种情况如下:
E全为1:这时如果M为0就表示无穷大。0 1111111100010000000000000000000。
E全为1: 1减去127或者1减去1023这之后作为指数求值都极小,所以表示0。
其余情况就正常减去中间值就行。
浮点数存储的不精确性
通过以上介绍我们可以知道并不是任何一个浮点数都是可以完全准确的表示出来的。
可以尝试一下将3.14转换一下,如果你准确将其存入私信我V你50。
