AI学习指南数学工具篇-核函数之高斯径向基核（Gaussian Radial Basis Function Kernel）

AI学习指南数学工具篇-核函数之高斯径向基核（Gaussian Radial Basis Function Kernel）

在机器学习和人工智能领域中，核方法是一种重要的技术，它通过核函数将原始的非线性问题转化为线性问题，从而使得一些传统的线性模型也能够处理复杂的非线性数据。在核方法中，高斯径向基核函数（Gaussian Radial Basis Function Kernel）是一种常用的核函数之一，它具有很好的非线性拟合能力，在处理分类、回归等问题时表现出色。

本篇博文将介绍高斯径向基核函数及其在核方法中的应用，包括对高斯径向基核函数的解释，其在支持向量机（SVM）中的使用等内容，并给出详细的示例来帮助读者更好地理解和运用高斯径向基核函数。

1. 高斯径向基核函数的介绍

高斯径向基核函数是一种常用的核函数，它的表达式为：$$k(x,x")=exp(-\frac{||x-x"|{|}^2}{2{\sigma }^2})$$其中，$x$和$x"$分别表示样本空间中的两个样本，$||x-x"||$表示两个样本之间的欧几里得距离，$\sigma$是高斯核函数的一个超参数，控制了核函数的宽度。

高斯径向基核函数的作用是将原始样本空间映射到一个无限维的特征空间中，并且具有很好的非线性拟合能力。在实际应用中，我们通常通过核技巧来计算在特征空间中的内积，从而避免显式地计算特征空间的转换。

2. 高斯径向基核函数在支持向量机中的应用

支持向量机（Support Vector Machine，SVM）是一种常用的机器学习算法，它通过最大化间隔来实现对样本的分类。在SVM中，我们可以使用高斯径向基核函数来处理线性不可分的问题，从而将原始的非线性分类问题转化为线性分类问题。

假设我们的原始数据集包含$n$个样本$\{(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),\cdots ,(x^{(n)},y^{(n)})\}$，其中$x^{(i)}$表示第$i$个样本的特征向量，$y^{(i)}$表示第$i$个样本的标签。我们的目标是学习一个最优的超平面来对样本进行分类。

对于非线性分类问题，我们可以使用高斯径向基核函数将原始特征空间映射到一个更高维的特征空间，并在新的特征空间中进行线性分类。具体来说，我们可以将原始特征$x^{(i)}$映射为$\varphi (x^{(i)})$，其中$\varphi (\cdot )$表示高斯径向基核函数的映射，然后在新的特征空间中学习一个最优的超平面来进行分类。

在SVM的优化问题中，我们需要计算样本在特征空间中的内积，而在使用高斯径向基核函数时，我们可以通过核技巧避免显式地计算特征空间的转换。具体来说，SVM的优化问题可以表示为：$$\underset{w,b,\xi }{\mathrm{argmin}}\frac{1}{2}||w|{|}^2+C\sum _{i=1}^n{\xi }_i$$$$\text{subject to }{y}^{(i)}(w\cdot \varphi (x^{(i)})+b)\ge 1-{\xi }_i,{\xi }_i\ge 0$$其中，$w$、$b$和$\xi$分别表示超平面的法向量、偏置项和松弛变量，$C$是一个正则化参数，控制了间隔的大小。

在使用高斯径向基核函数时，我们的优化问题中的内积项可以表示为：$$\varphi (x^{(i)})\cdot \varphi (x^{(j)})=exp(-\frac{||x^{(i)}-x^{(j)}|{|}^2}{2{\sigma }^2})$$这样，我们就可以通过核技巧来计算在特征空间中的内积，而不需要显式地计算特征空间的转换。从而大大简化了优化问题的求解过程。

3. 高斯径向基核函数的示例

为了更好地理解高斯径向基核函数及其在核方法中的应用，我们给出一个简单的示例来说明高斯径向基核函数的作用。

假设我们的原始样本空间是一维空间，我们的目标是学习一个最优的超平面将样本进行分类。然而，原始样本空间中的样本并不是线性可分的，我们可以使用高斯径向基核函数将原始样本映射到一个更高维的特征空间中，并在新的特征空间中进行线性分类。

import numpy as np import matplotlib.pyplot as plt  # 生成原始样本数据 X = np.linspace(-5, 5, 100).reshape(-1, 1) y = np.sin(X).reshape(-1) y[y > 0] = 1 y[y <= 0] = -1  # 使用高斯径向基核函数将样本映射到更高维的特征空间 def gaussian_rbf_kernel(x, x_prime, sigma=1.0):     return np.exp(-np.linalg.norm(x - x_prime)**2 / (2 * sigma**2))  X_new = np.array([gaussian_rbf_kernel(x, 0) for x in X]).reshape(-1, 1)  # 在新的特征空间中学习一个最优的超平面来进行分类 plt.scatter(X, X_new, c=y, cmap=plt.cm.Paired, s=20) plt.xlabel("Original Feature Space") plt.ylabel("Transformed Feature Space with Gaussian RBF Kernel") plt.show()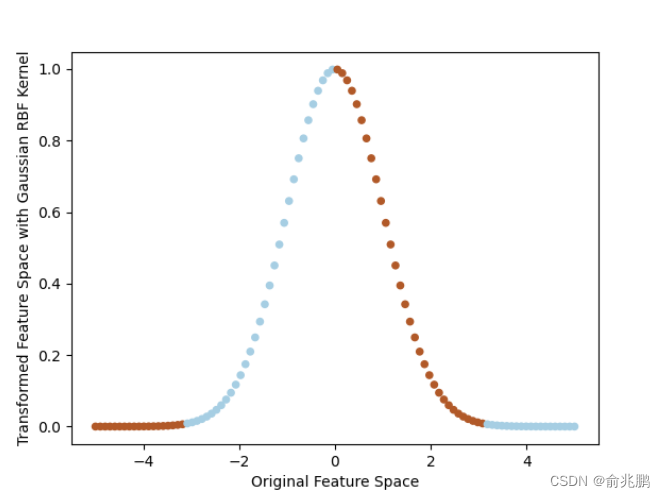 

上面的示例中，我们生成了原始的一维样本数据，并使用高斯径向基核函数将样本映射到更高维的特征空间中。然后我们通过散点图的方式展示了原始特征空间与新的特征空间的关系，从而直观地展示了高斯径向基核函数的作用。

4. 总结

高斯径向基核函数是一种常用的核函数，它具有很好的非线性拟合能力，在核方法中得到了广泛的应用。本篇博文对高斯径向基核函数进行了详细的介绍，并给出了在支持向量机中的应用和一个简单的示例，希望能够帮助读者更好地理解和运用高斯径向基核函数。

在实际应用中，我们可以根据具体的问题和数据特点来选择合适的核函数，从而实现对复杂非线性问题的处理。同时，对于高斯径向基核函数和其他核函数的理解和运用，也是学习和应用核方法的关键之处。希望本篇博文能够对读者有所帮助，为大家在人工智能和机器学习领域的学习和研究提供一些参考和借鉴。