轮转数组
题目描述:
给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3 输出:[5,6,7,1,2,3,4]解释: 向右轮转 1 步:[7,1,2,3,4,5,6]向右轮转 2 步:[6,7,1,2,3,4,5]向右轮转 3 步:[5,6,7,1,2,3,4]
示例 2:
输入:nums = [-1,-100,3,99], k = 2 输出:[3,99,-1,-100] 解释: 向右轮转 1 步: [99,-1,-100,3] 向右轮转 2 步: [3,99,-1,-100]
提示:
1 <= nums.length <= 105-231 <= nums[i] <= 231 - 10 <= k <= 105
进阶:
- 尽可能想出更多的解决方案,至少有 三种 不同的方法可以解决这个问题。
- 你可以使用空间复杂度为
O(1)的 原地 算法解决这个问题吗?
方法一思路分析:
使用一个额外的数组 res 来暂存旋转后的结果,然后再将这个结果复制回原数组 nums。
具体步骤:
初始化:首先,获取数组
nums的长度n,并创建一个同样大小的数组res用于暂存旋转后的结果。旋转:通过一个循环,遍历原数组
nums中的每个元素。对于每个元素nums[i],计算它旋转k步后应该在res数组中的位置。这个位置通过(i + k) % n来计算,以确保索引在有效范围内内循环。复制回原数组:使用
System.arraycopy方法将旋转后的结果从res数组复制回原数组nums。
代码实现:
class Solution { public void rotate(int[] nums, int k) { int n = nums.length; int[] res = new int [n]; for(int i = 0; i<n; i++){ res[(i + k) % n] = nums[i]; } System.arraycopy(res, 0, nums, 0, n); } } 方法二思路分析:
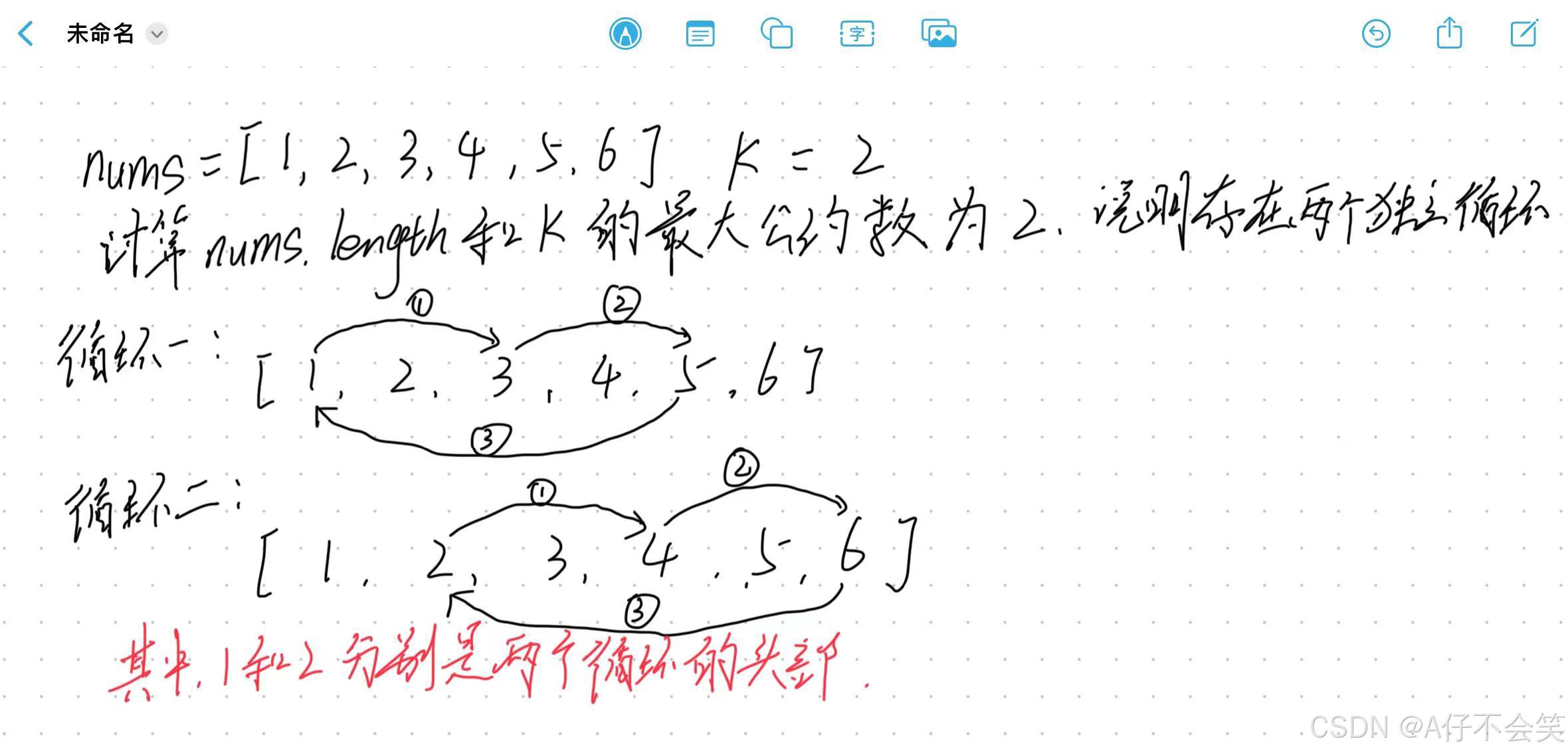
使用环状替换法,在旋转数组时,某些元素会形成一个或多个循环,这些循环的长度是 k 和数组长度 n 的最大公约数(GCD)。
具体步骤如下:
首先,我们计算
k和n的最大公约数(GCD),记为count。这个count表示了数组中独立循环的个数,每个循环中的元素个数也是count。然后,我们遍历从
0到count-1的每个start索引,以start为起点的每个元素都会参与到一个长度为count的循环中。对于每个
start,我们使用一个循环来找到并替换这个循环中的所有元素。我们使用变量current来跟踪当前正在处理的元素索引,prev来保存前一个元素的值,以便将其放入next索引的位置。在循环中,我们计算
next索引,它是current + k对n取模的结果。然后,我们将prev(即前一个元素的值)赋给nums[next],并更新prev为nums[next](即我们刚刚覆盖的那个值),同时更新current为next,以便进行下一次迭代。循环继续,直到我们回到起始索引
start,这时我们就完成了一个循环的替换。最后,我们继续对下一个
start索引进行相同的操作,直到遍历完所有的count个独立循环。
例如:
代码实现:
class Solution { public void rotate(int[] nums, int k) { int n = nums.length; k = k % n; // 将k对n取模,因为如果k是n的倍数,则旋转后的数组与原数组相同 int count = gcd(k, n); // 计算k和n的最大公约数,这决定了独立循环的个数 // 遍历每个独立循环的起始点 for (int start = 0; start < count; ++start) { int current = start; // 当前正在处理的元素索引 int prev = nums[start]; // 保存当前索引位置的元素值,用于后续交换 // 遍历当前循环中的所有元素,进行旋转 do { int next = (current + k) % n; // 计算下一个元素的索引 int temp = nums[next]; // 保存下一个元素的值 nums[next] = prev; // 将前一个元素的值放到当前索引位置 prev = temp; // 更新prev为下一个元素的值,以便在下次迭代中使用 current = next; // 更新current为下一个元素的索引 // 当回到起始点时,说明当前循环中的所有元素都已经被正确旋转 } while (start != current); } } public int gcd(int x, int y) { // 使用欧几里得算法递归计算最大公约数 return y > 0 ? gcd(y, x % y) : x; } }方法三思路分析:
使用整体翻转
反转整个数组:首先,将整个数组进行反转。这样,原本在数组末尾的元素会被移动到数组的开始位置,但顺序是反的。
反转前k个元素:然后,反转数组的前
k % n个元素(其中n是数组的长度,因为k可能大于数组长度,所以需要取模)。这样,前k个元素就被移动到了它们旋转后的正确位置上,但顺序仍然是反的。反转剩余的元素:最后,反转数组中剩下的元素(即除了前
k % n个元素之外的元素)。这样,剩下的元素也会被移动到它们旋转后的正确位置上,并且整个数组的顺序也恢复了正常。
代码实现:
class Solution { public void rotate(int[] nums, int k) { k %= nums.length; reverse(nums,0,nums.length - 1); reverse(nums,0,k-1); reverse(nums,k,nums.length - 1); } //反转函数 public void reverse(int[] nums, int start, int end){ while (start < end) { int temp = nums[start]; nums[start] = nums[end]; nums[end] = temp; start += 1; end -= 1; } } }