🔒文章目录:
1.❤️❤️前言~🥳🎉🎉🎉
Hello, Hello~ 亲爱的朋友们👋👋,这里是E绵绵呀✍️✍️。
如果你喜欢这篇文章,请别吝啬你的点赞❤️❤️和收藏📖📖。如果你对我的内容感兴趣,记得关注我👀👀以便不错过每一篇精彩。
当然,如果在阅读中发现任何问题或疑问,我非常欢迎你在评论区留言指正🗨️🗨️。让我们共同努力,一起进步!
加油,一起CHIN UP!💪💪
🔗个人主页:E绵绵的博客
📚所属专栏:1. JAVA知识点专栏
深入探索JAVA的核心概念与技术细节
2.JAVA题目练习
实战演练,巩固JAVA编程技能
3.c语言知识点专栏
揭示c语言的底层逻辑与高级特性
4.c语言题目练习
挑战自我,提升c语言编程能力
📘 持续更新中,敬请期待❤️❤️
这篇文章将给大家介绍七大排序,并且还会介绍三大非基于比较的排序(计数排序+基数排序+桶排序),干货满满,还请大家认真看下去。
借鉴的相关文章: 超详细八大排序+基数排序
这篇文章写的很好!作者很用心的在做了,大家可以关注下该作者!多多支持下!
2.排序的概念
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
以下是我们常见的七大排序
下面我们逐一讲解。
3.七大排序
3.1 直接插入排序(插入排序)
直接插入排序是一种简单的插入排序法,基本思想是:把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。
以下是动图演示:
这很好理解,就是将数组中的每一个数字拿出来往前扫描,若大于则插在其后,一直反复操作,直到拿完所有的数为止。
代码如下:
public class Sort1 { public static void main(String[] args) { int[] array={4,9,5,7,3,4,20,-4,82,35,100}; shell(array); System.out.println(Arrays.toString(array)); } public static void shell(int[] array){ for (int i = 0; i <array.length-1 ; i++) { int temp=array[i+1]; int j=i; for (; j >=0 ; j--) { if(array[j]>temp) break; else array[j+1]=array[j]; } array[j+1]=temp; } } }
对于直接插入排序,在最坏情况下,也就是数组为降序时,此时要进行升序操作,时间复杂度将达到O(N^2),而在最好的情况下,插入排序的时间复杂度仅为O(N),因此数学家希尔想了一个办法,若通过某种办法使得待排序列接近有序,此时再来进行一次直接插入排序,是不是更有效了呢?于是就有了下面的希尔排序
3.2 希尔排序(插入排序)
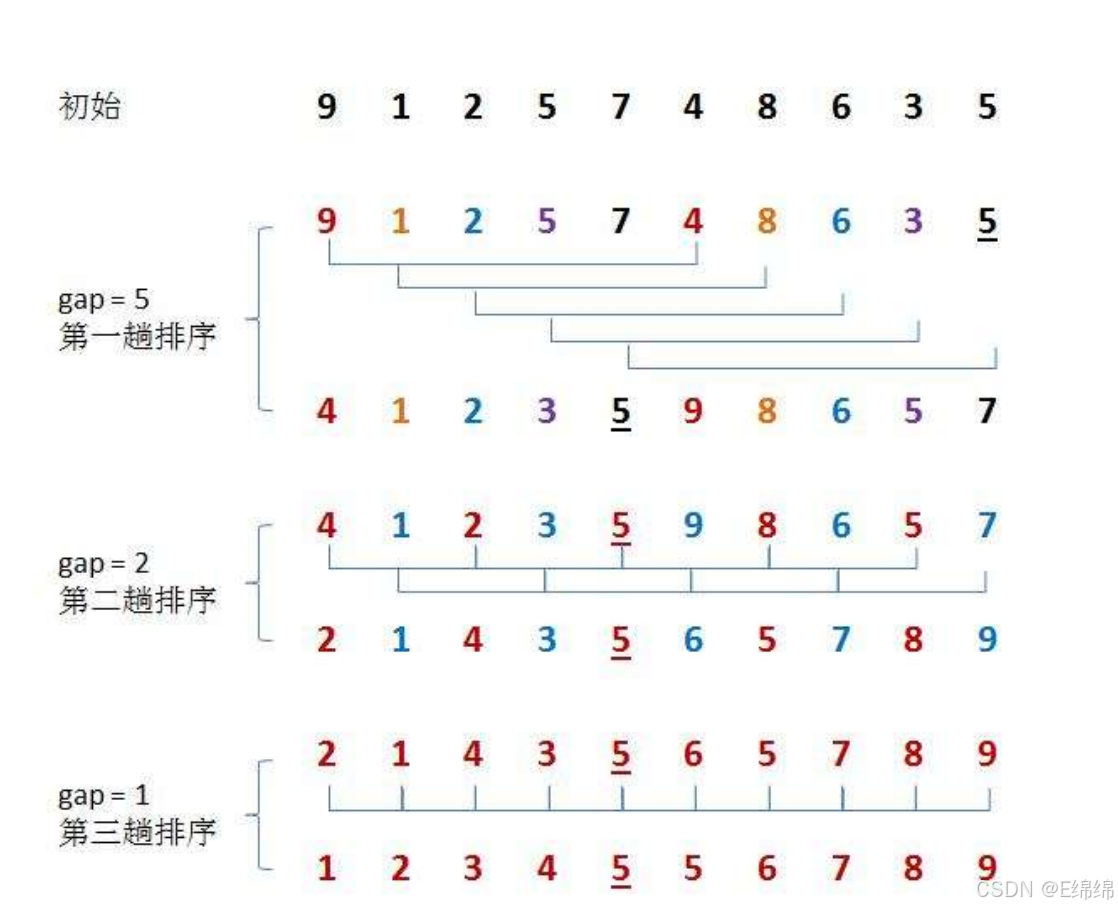
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个小于N的整数gap作为一个增量,把待排序序列中所有数据为gap的数放在一组,并对每一组进行直接插入排序,然后缩小增量,重复上述过程,直至gap==1,此时我们得到一个接近有序的序列,因此对整体数据进行一次插入排序时,时间复杂度将大大缩减。
增量gap呈现从大到小的变化,使得序列一步步接近有序。
希尔排序的特性总结:
1. 希尔排序是对直接插入排序的优化。
2. 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。
3. 希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些树中给出的希尔排序的时间复杂度都不固定:
希尔排序具体操作图如下:
具体代码如下:
// 从大往小 希尔排序 public class Sort2 { public static void main(String[] args) { int[] array={4,9,-200,7,3,53,20,-4,82,35,100}; sort(array); System.out.println(Arrays.toString(array)); } public static void sort(int[] array){ for (int i = array.length; i>1 ; ) { i/=2; shell(array,i); } } public static void shell(int[] array,int tam){ for (int i = 0; i <array.length-tam ; i++) { int temp=array[i+tam]; int j=i; for (; j >=0 ; j-=tam) { if(array[j]>temp) break; else array[j+tam]=array[j]; } array[j+tam]=temp; } } }
3.3 直接选择排序(选择排序)
直接选择排序思路很简单,从待排序列中选出最小值,放在序列的起始位置,直到全部扫描完。 上图是其动图,如下是其代码。
//直接选择排序 public class Sort3 { public static void main(String[] args) { int[] arr=new int[10]; Random random=new Random(); for (int i = 0; i <10 ; i++) { arr[i]=random.nextInt(100); } System.out.println(Arrays.toString(arr)); shell(arr); System.out.println(Arrays.toString(arr)); } //从大往小 public static void shell(int[] arr){ for (int j = 0; j <arr.length ; j++) { int a = j; for (int i = j+1; i <arr.length ; i++) { if (arr[i]>arr[j]) j=i; } int temp=arr[a]; arr[a]=arr[j]; arr[j]=temp; j=a; } }}
3.4 堆排序(选择排序)
对于堆排序,我们也讲过,在讲堆的文章中提过了堆排序。
如果你想要对堆有具体的了解,请看以下文章:
作者个人认为:
对于大家普遍认为的堆排序,都是自己模拟一个堆,而后再模拟实现向上转型,从而排序好,我个人认为过于麻烦。我们可以直接使用PriorityQueue去创建堆而后使用其中自带的方法去完成排序,就没有这么麻烦,并且达到一样的效果。
所以代码应该是:
//堆排序,从大变小 public class Sort4 { public static void main(String[] args) { int[] arr=new int[10]; Random random=new Random(); for (int i = 0; i <10 ; i++) { arr[i]=random.nextInt(100); } System.out.println(Arrays.toString(arr)); shell(arr); System.out.println(Arrays.toString(arr)); } public static void shell(int[] arr){ PriorityQueue<Integer> priorityQueue=new PriorityQueue<>(new Int()); for (int i= 0; i <arr.length ; ++i) { priorityQueue.offer(arr[i]); } for (int i = 0; i <arr.length ; i++) { arr[i]=priorityQueue.poll(); } } } class Int implements Comparator<Integer> { @Override public int compare(Integer o1, Integer o2) { return o2-o1; } }
如上代码如果看不懂的话可以看下作者发布过的对于堆的讲解的两篇文章。
如果你实在想要自己模拟实现一个堆并且自己模拟实现向上转型的话,
建议看看这篇文章: 超详细八大排序+基数排序
3.5 冒泡排序(交换排序)
“冒泡排序(Bubble Sort),是一种计算机科学领域的较简单的排序算法。 它重复地走访过要排序的元素列,依次比较两个相邻的元素,如果顺序(如从大到小、首字母从Z到A)错误就把他们交换过来。走访元素的工作是重复地进行,直到没有相邻元素需要交换,也就是说该元素列已经排序完成。 这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端(升序或降序排列),就如同碳酸饮料中二氧化碳的气泡最终会上浮到顶端一样,故名“冒泡排序”。
冒泡排序是我们的老熟人了,就不多讲了,直接上代码
//冒泡排序 从大到小 public class Sort5 { public static void main(String[] args) { int[] arr=new int[10]; Random random=new Random(); for (int i = 0; i <10 ; i++) { arr[i]=random.nextInt(100); } System.out.println(Arrays.toString(arr)); shell(arr); System.out.println(Arrays.toString(arr)); } public static void shell(int[] arr){ for (int i = 0; i <arr.length-1 ; i++) { for (int j = 0; j <arr.length-i-1 ; j++) { if (arr[j]<arr[j+1]) swap(arr,j,j+1); } } } public static void swap(int[] arr,int a,int b) { int temp=arr[a]; arr[a]=arr[b]; arr[b]=temp; } }
3.6 快速排序(交换排序)
单趟排序Hoare版本
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
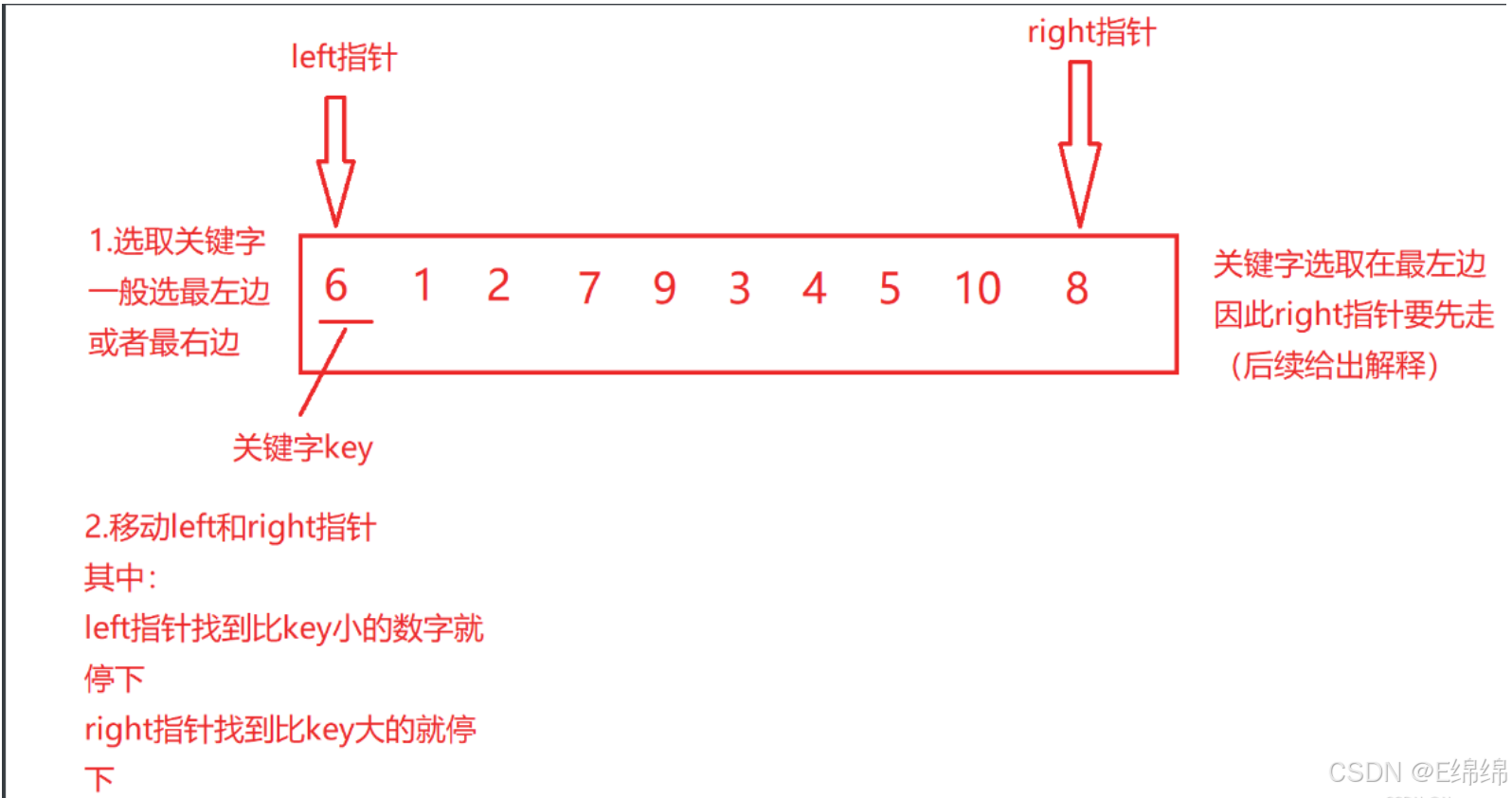
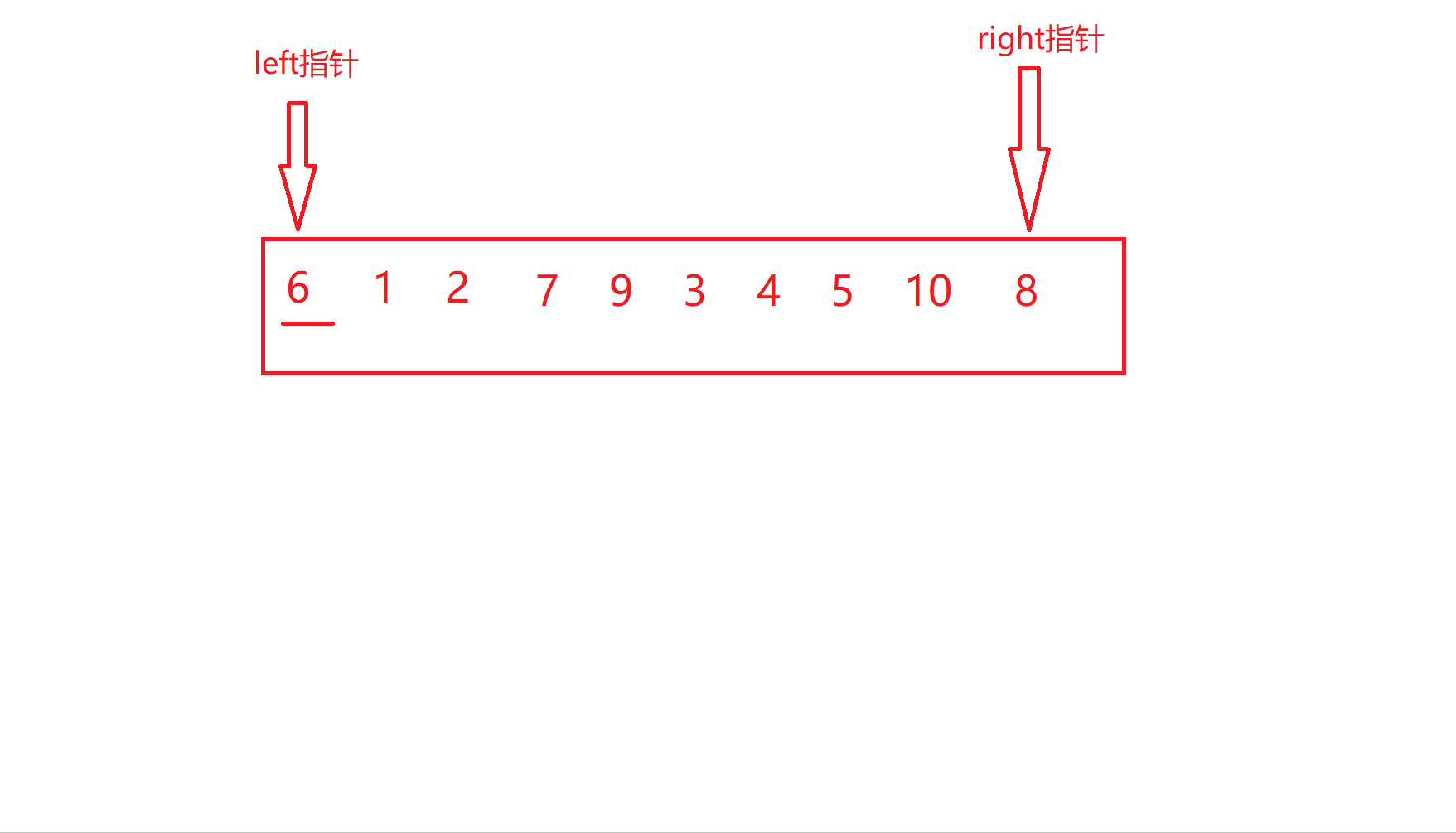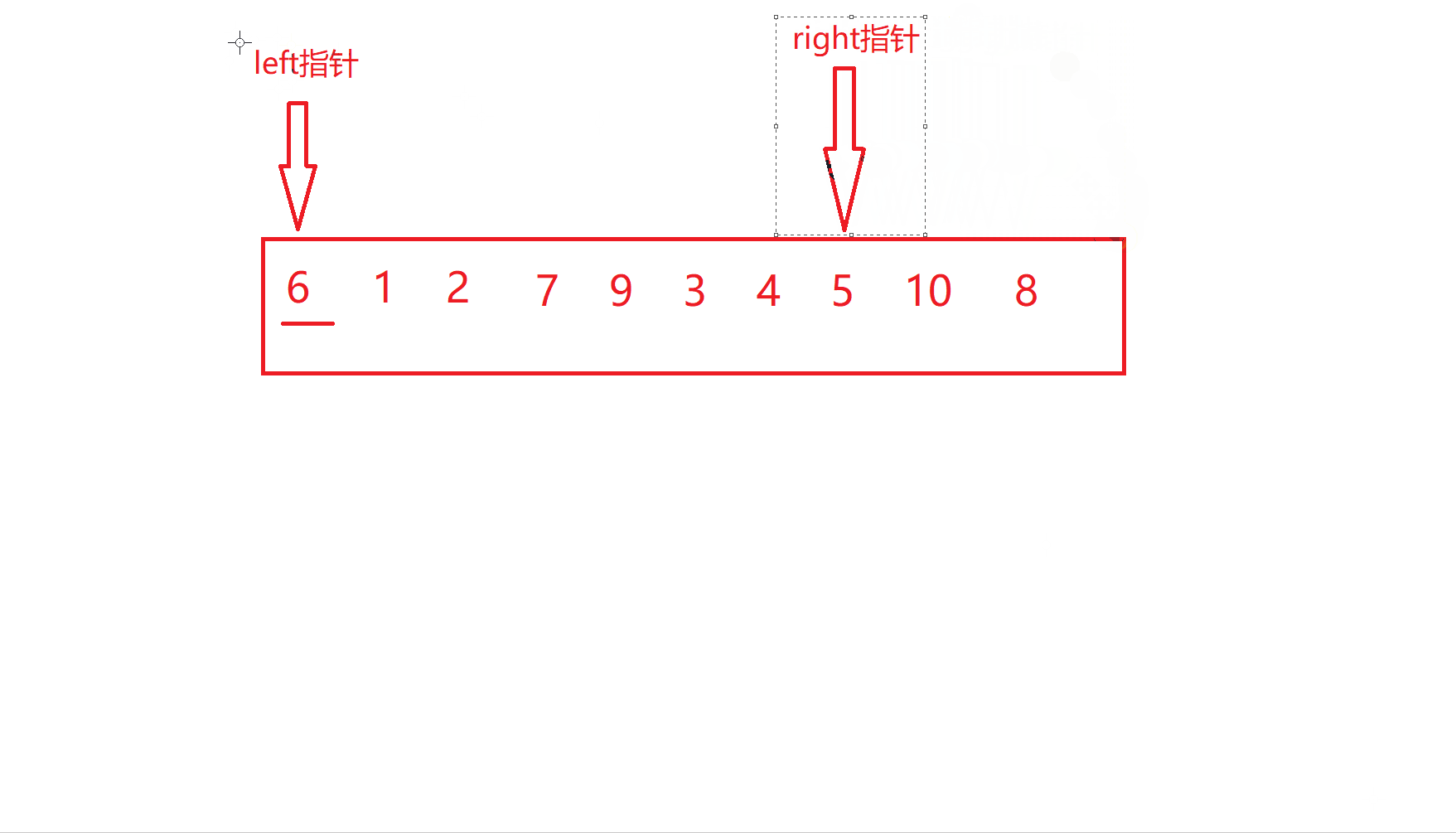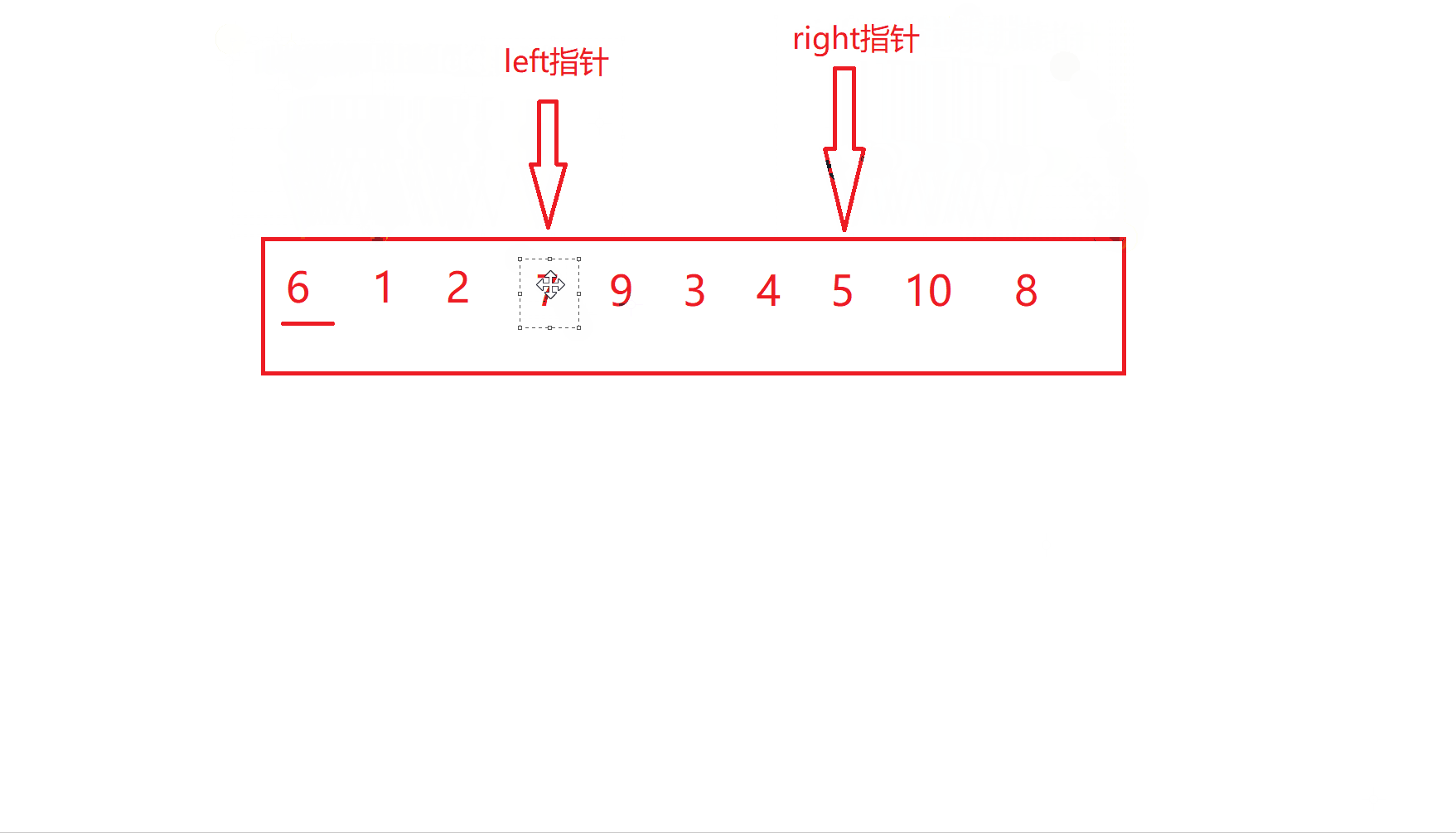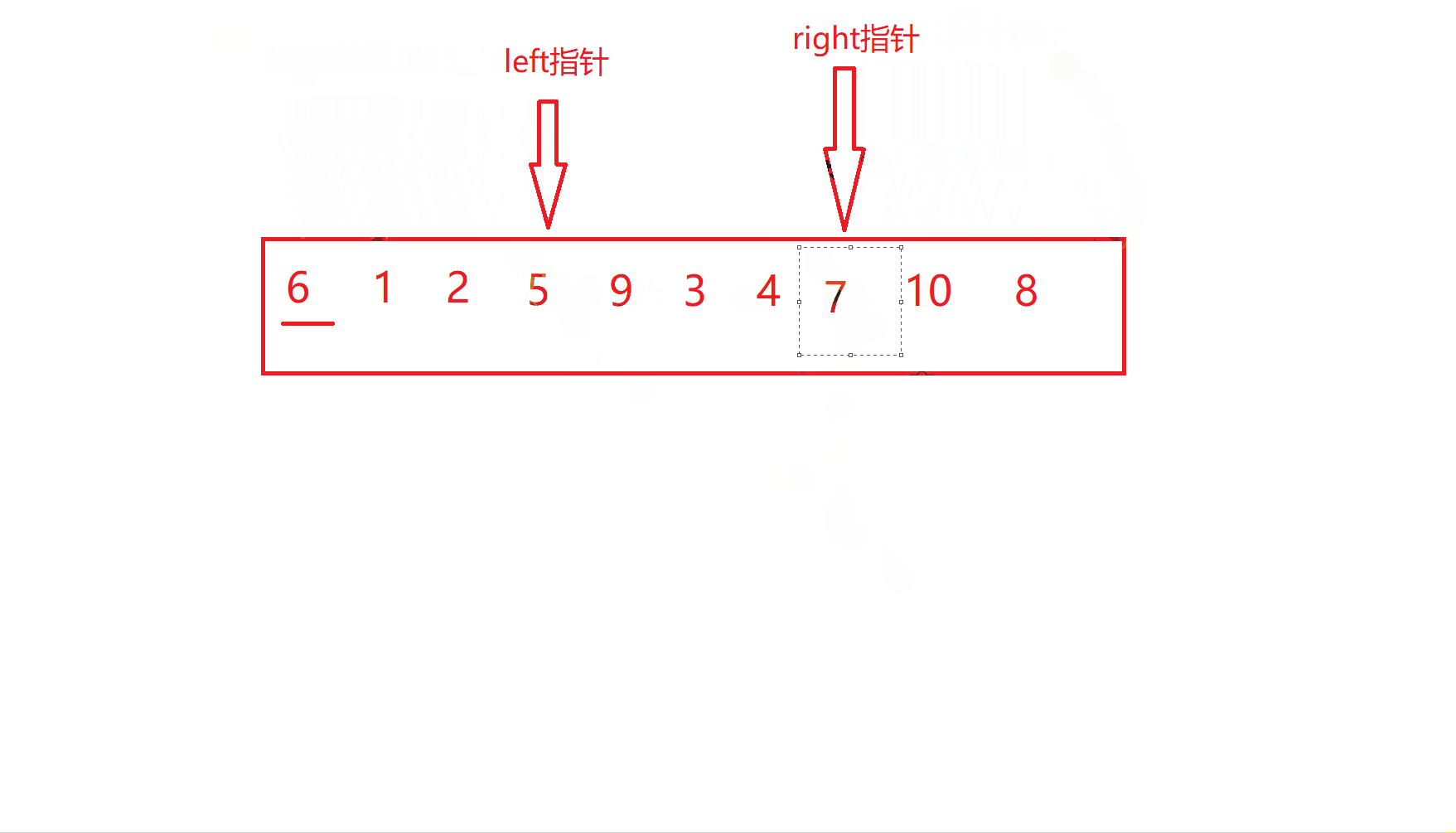
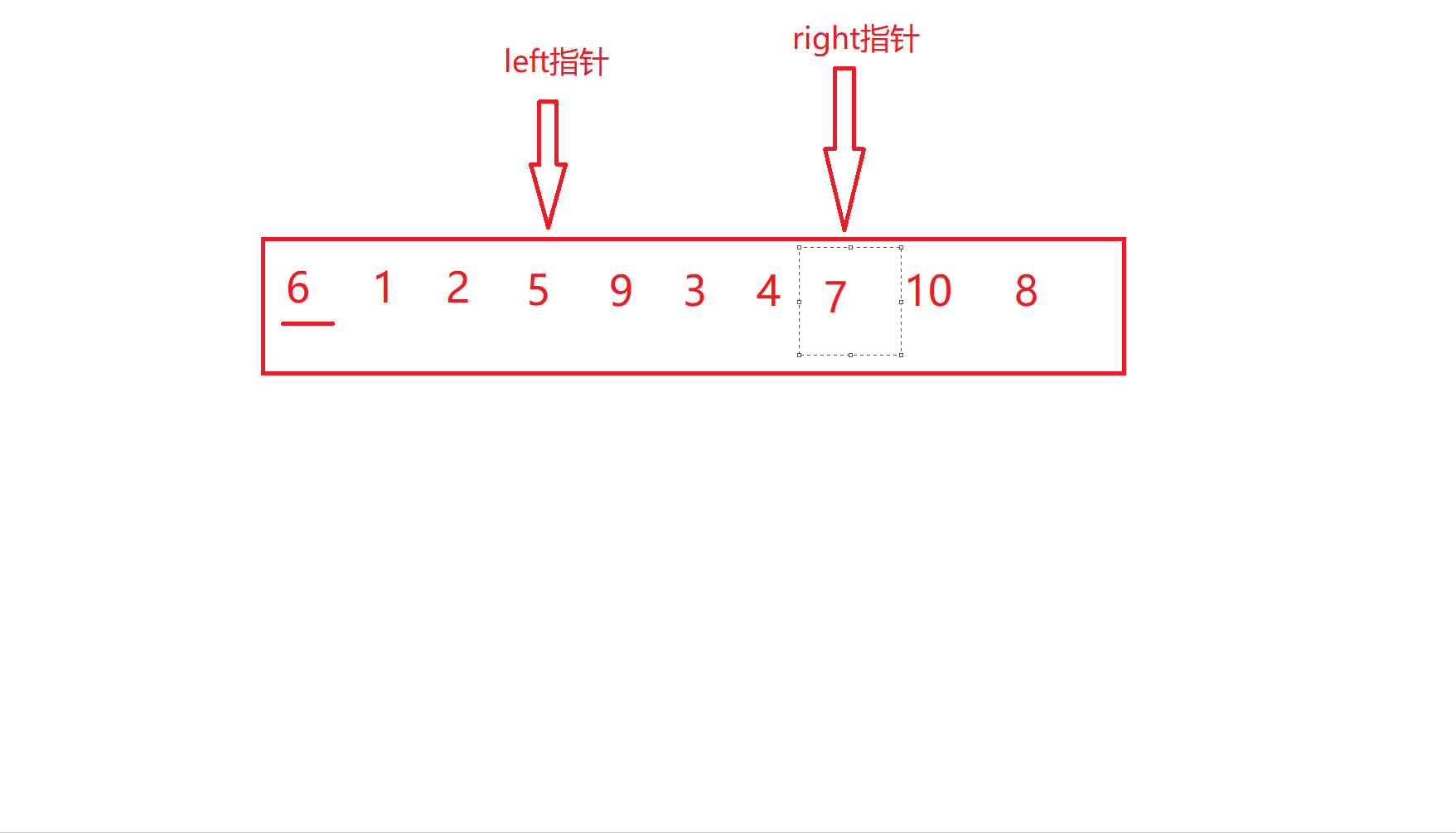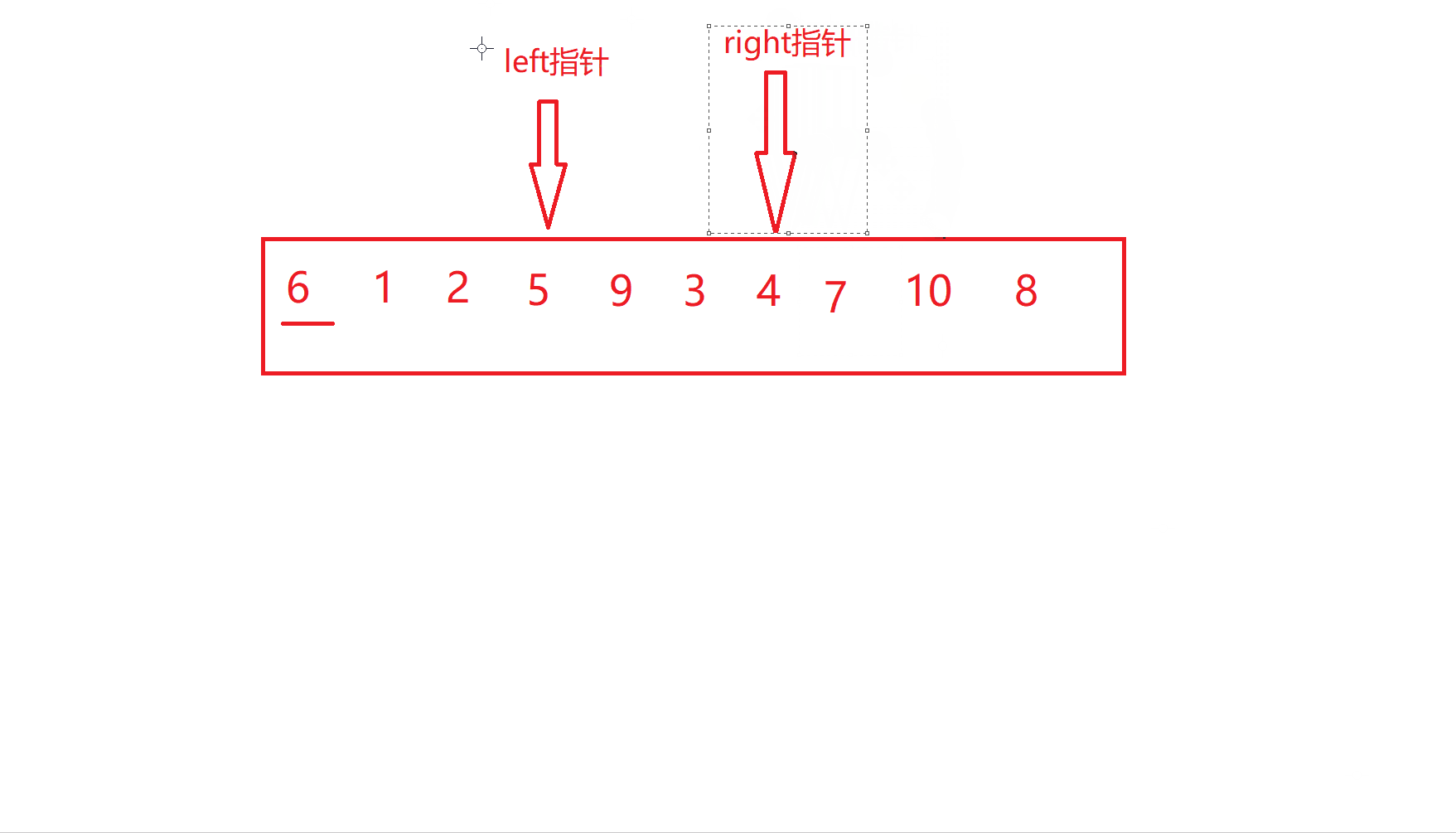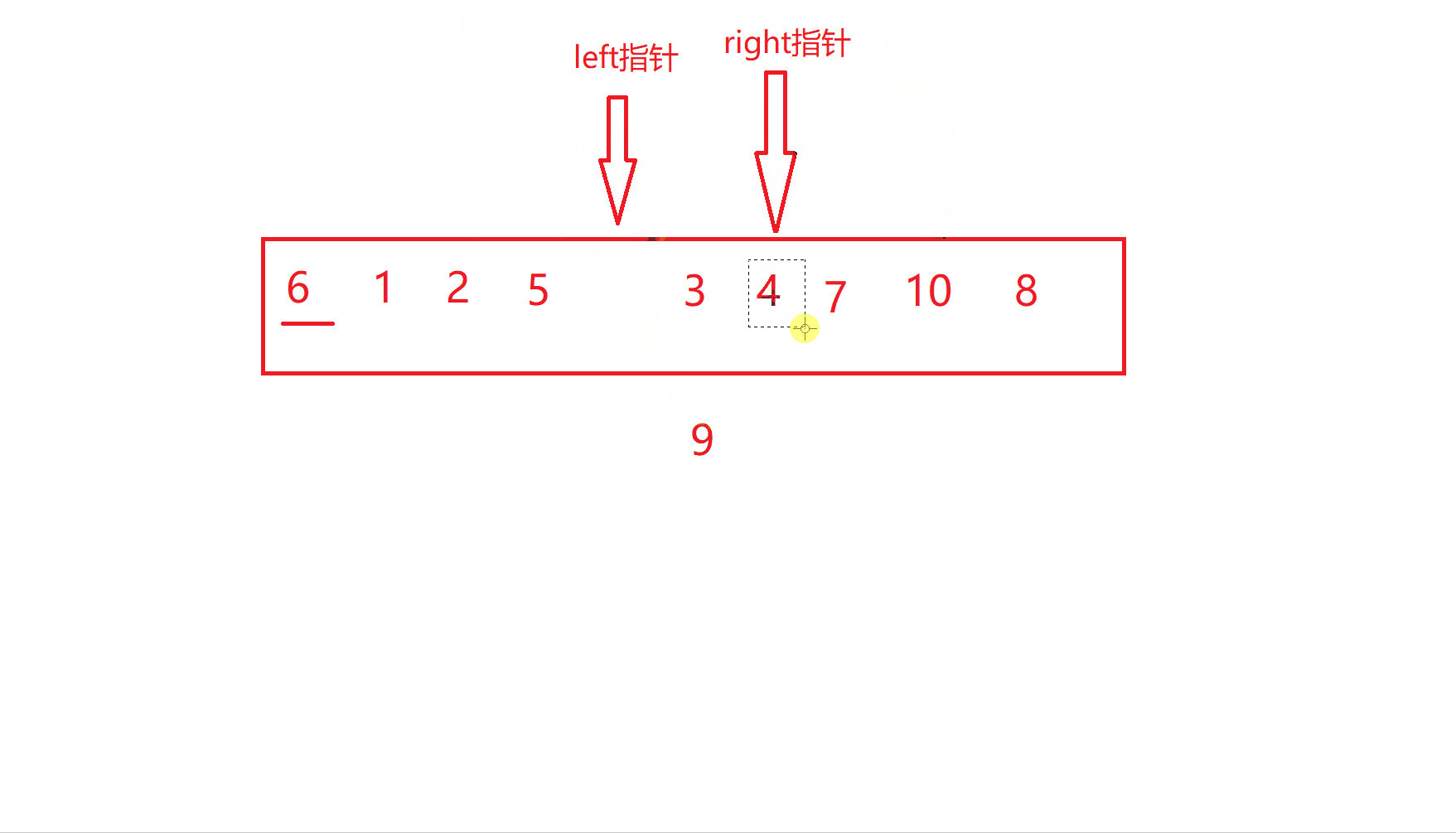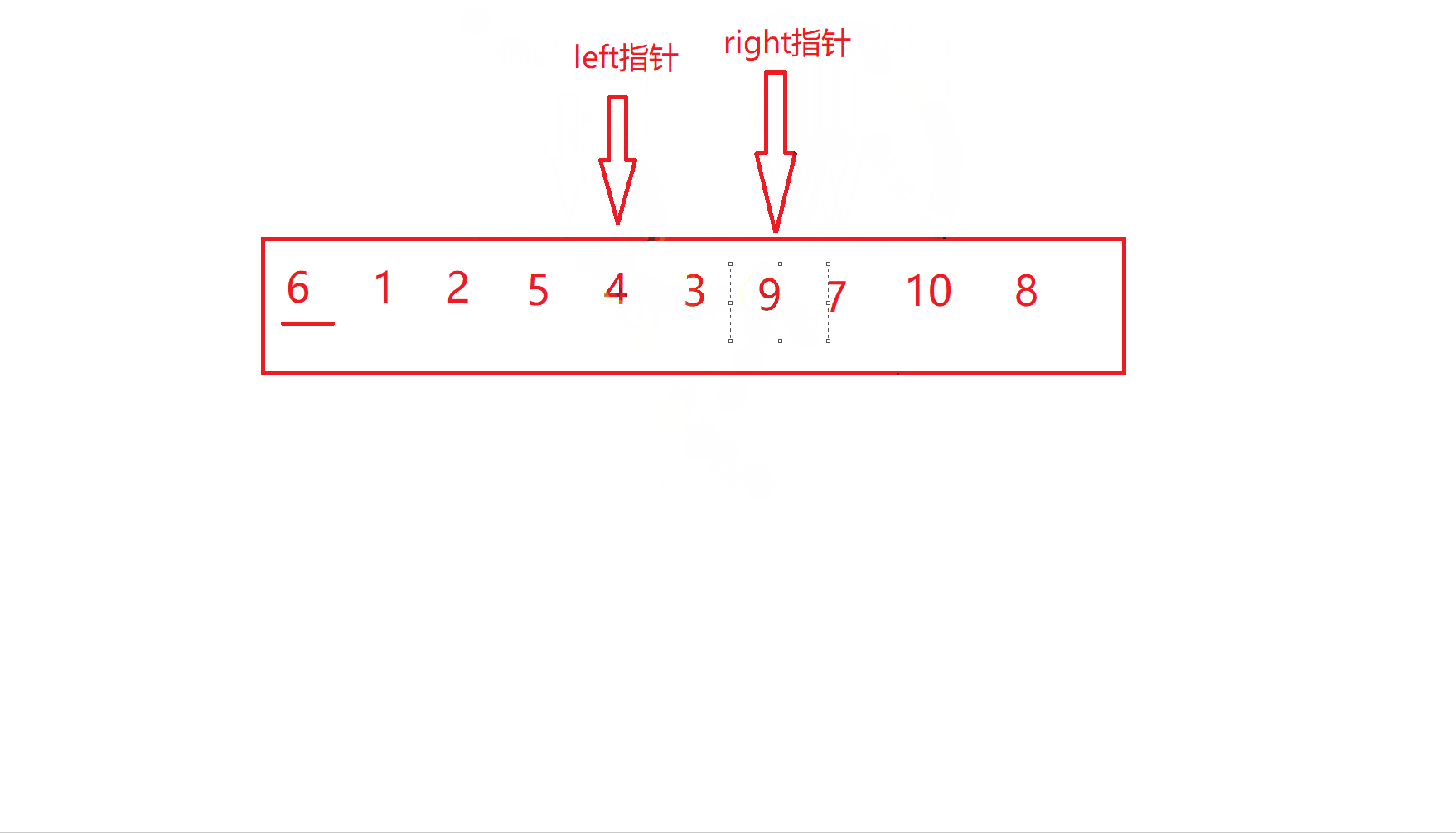
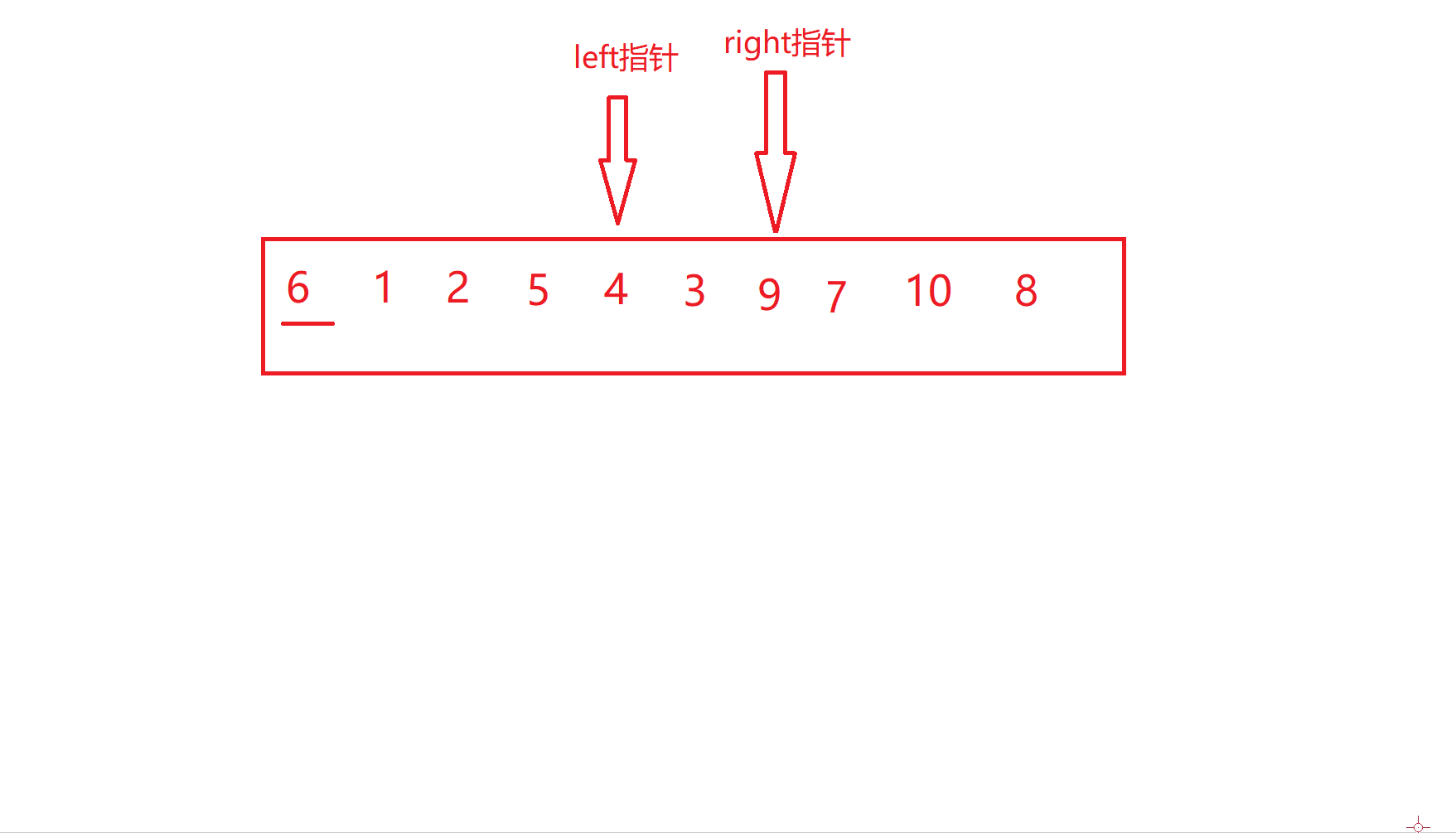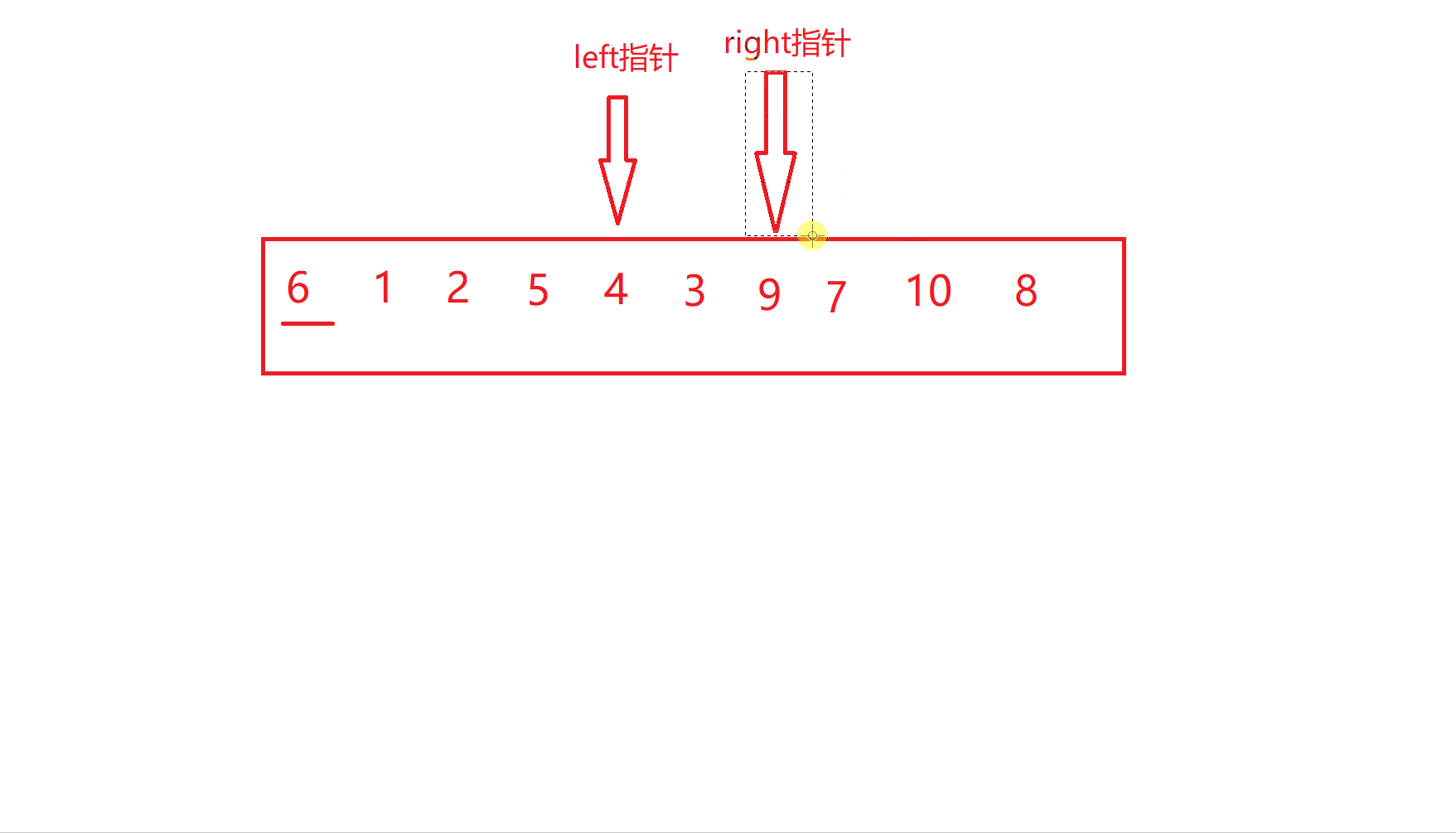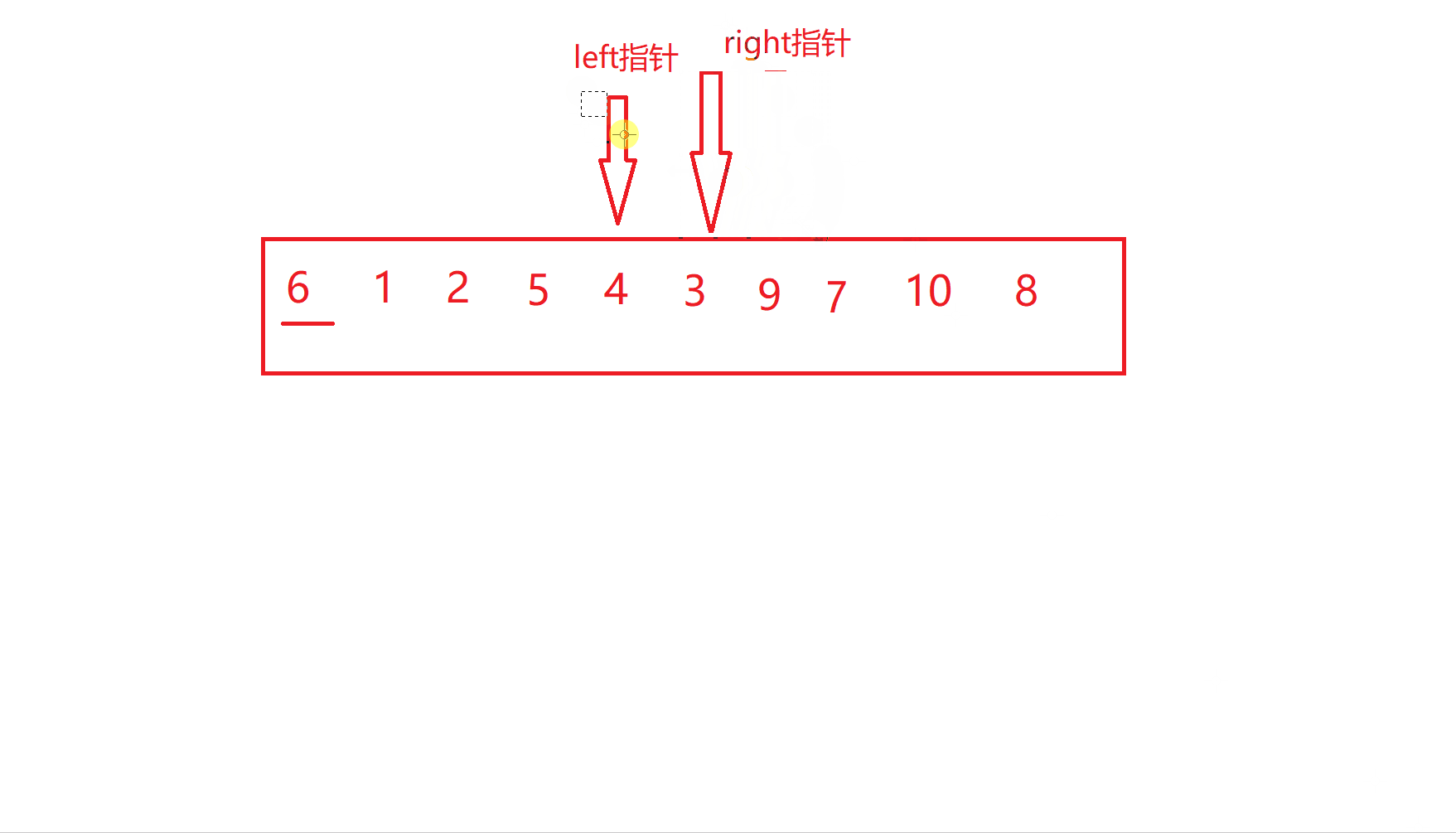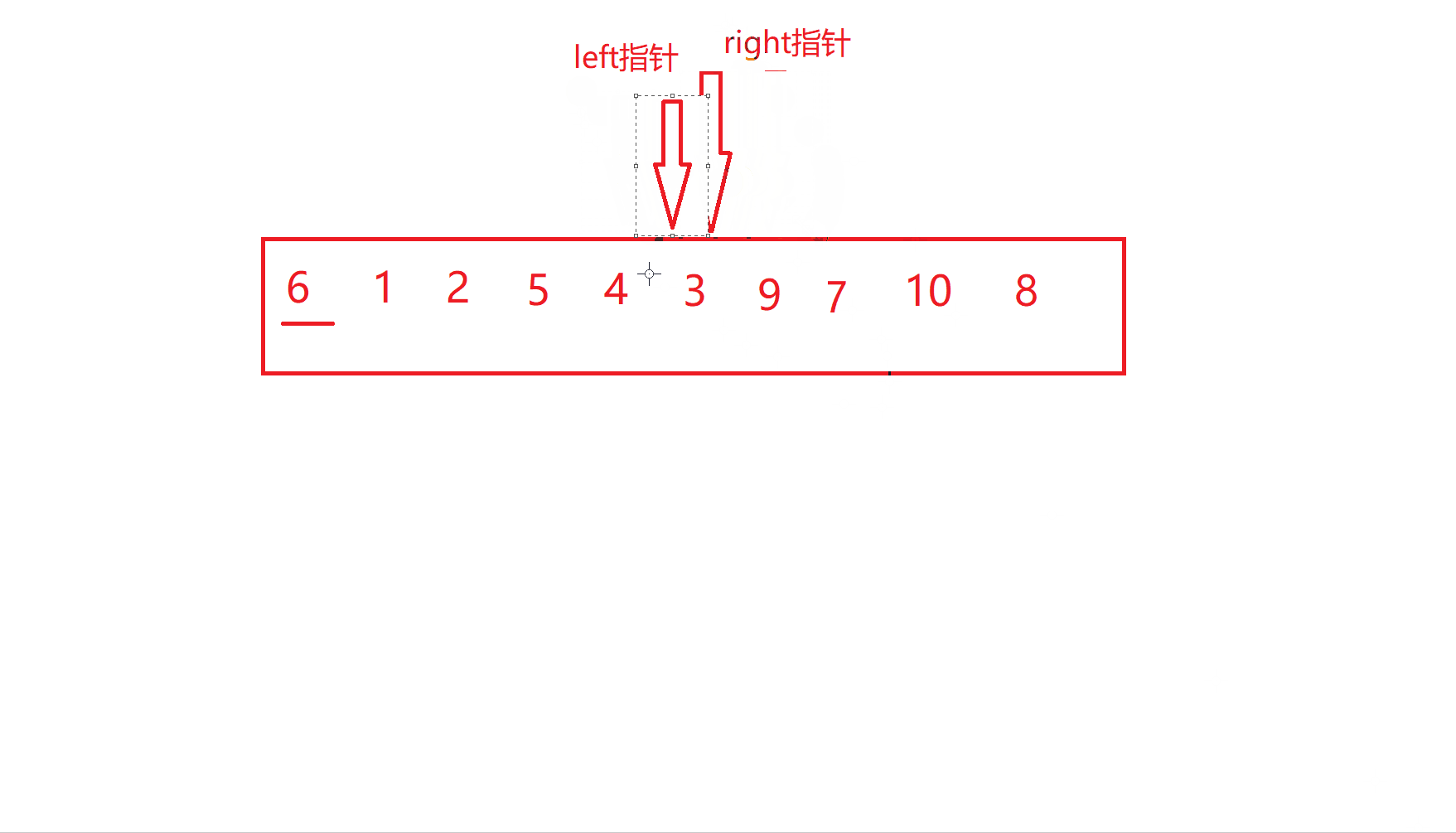
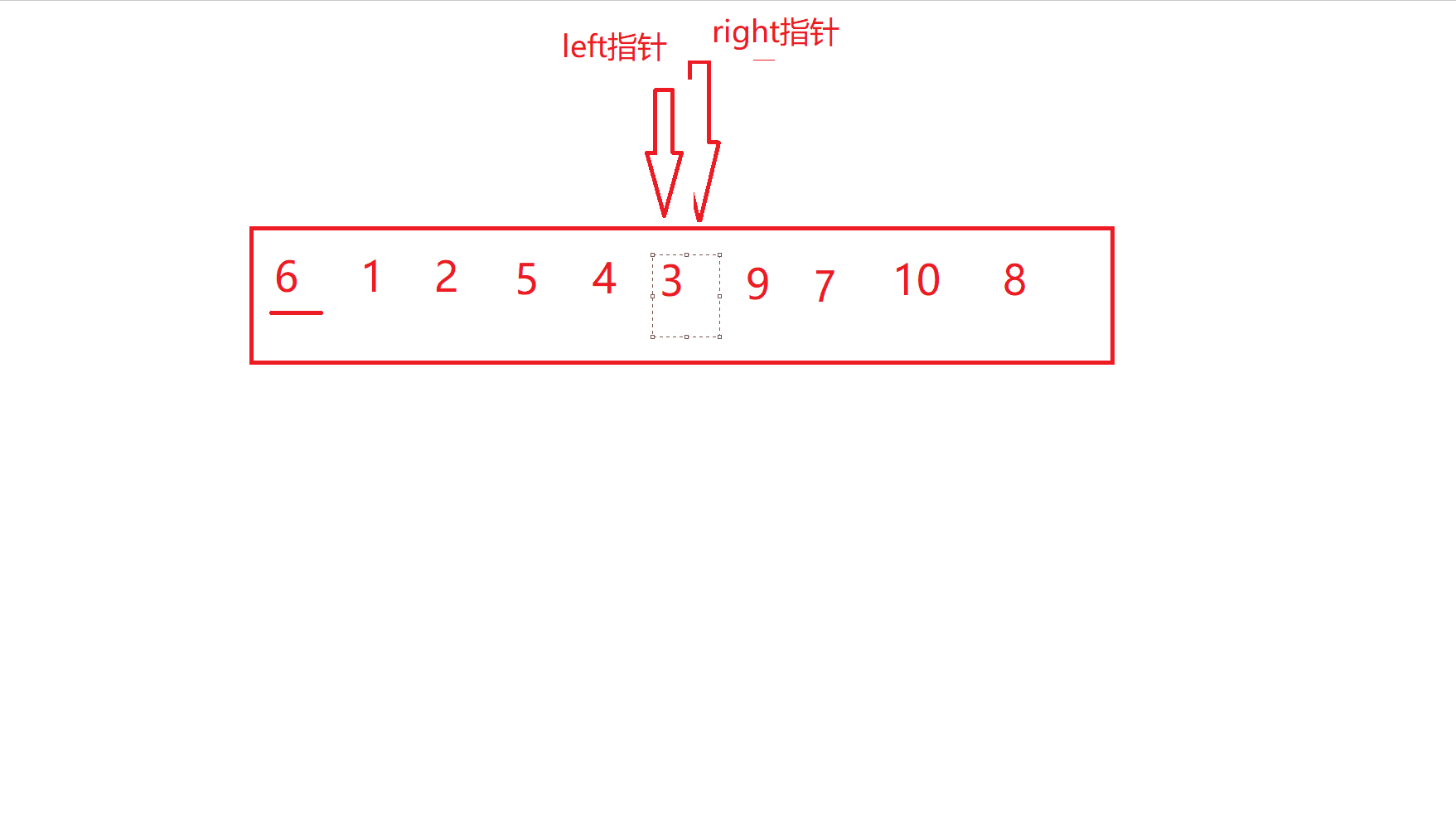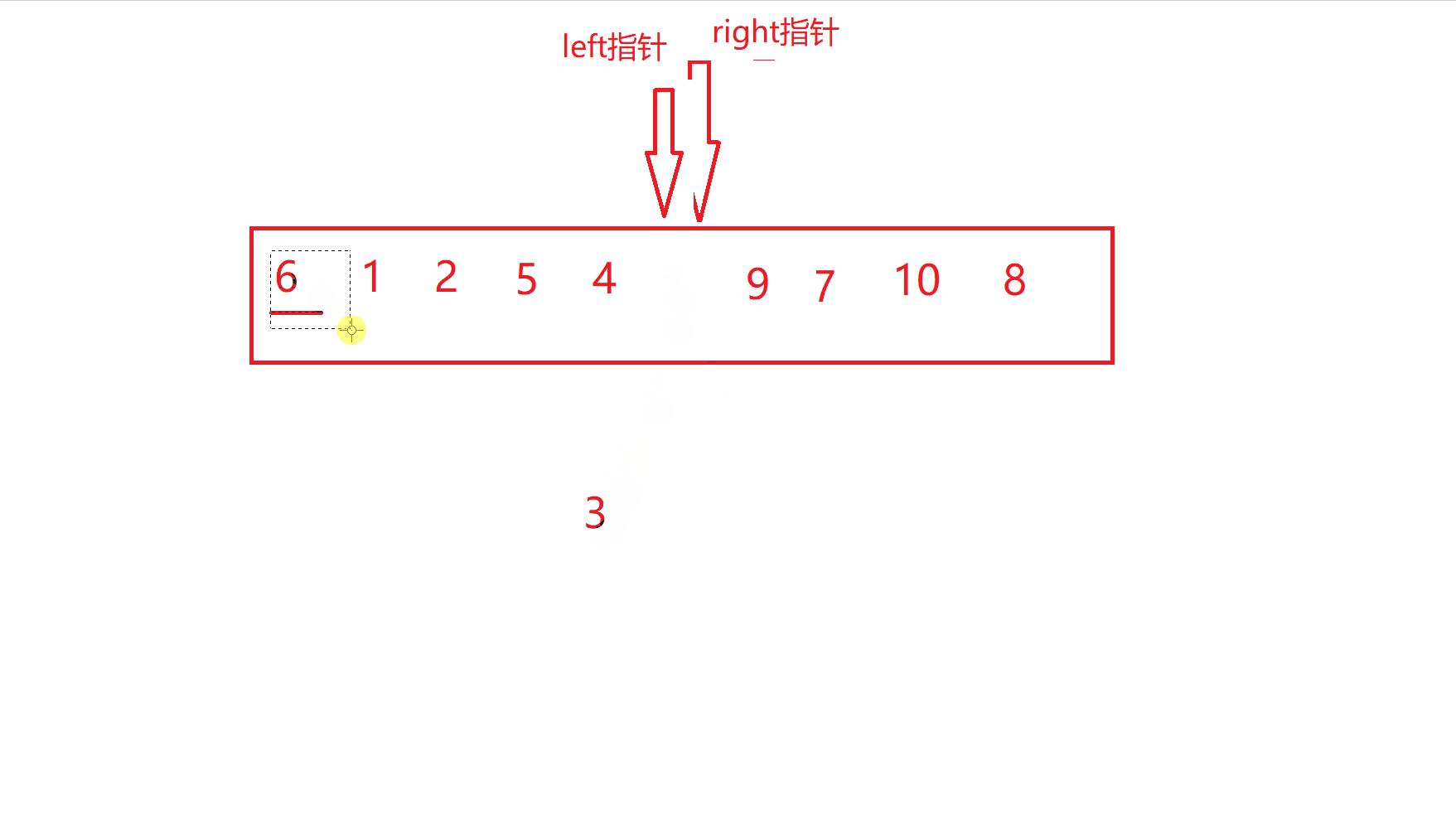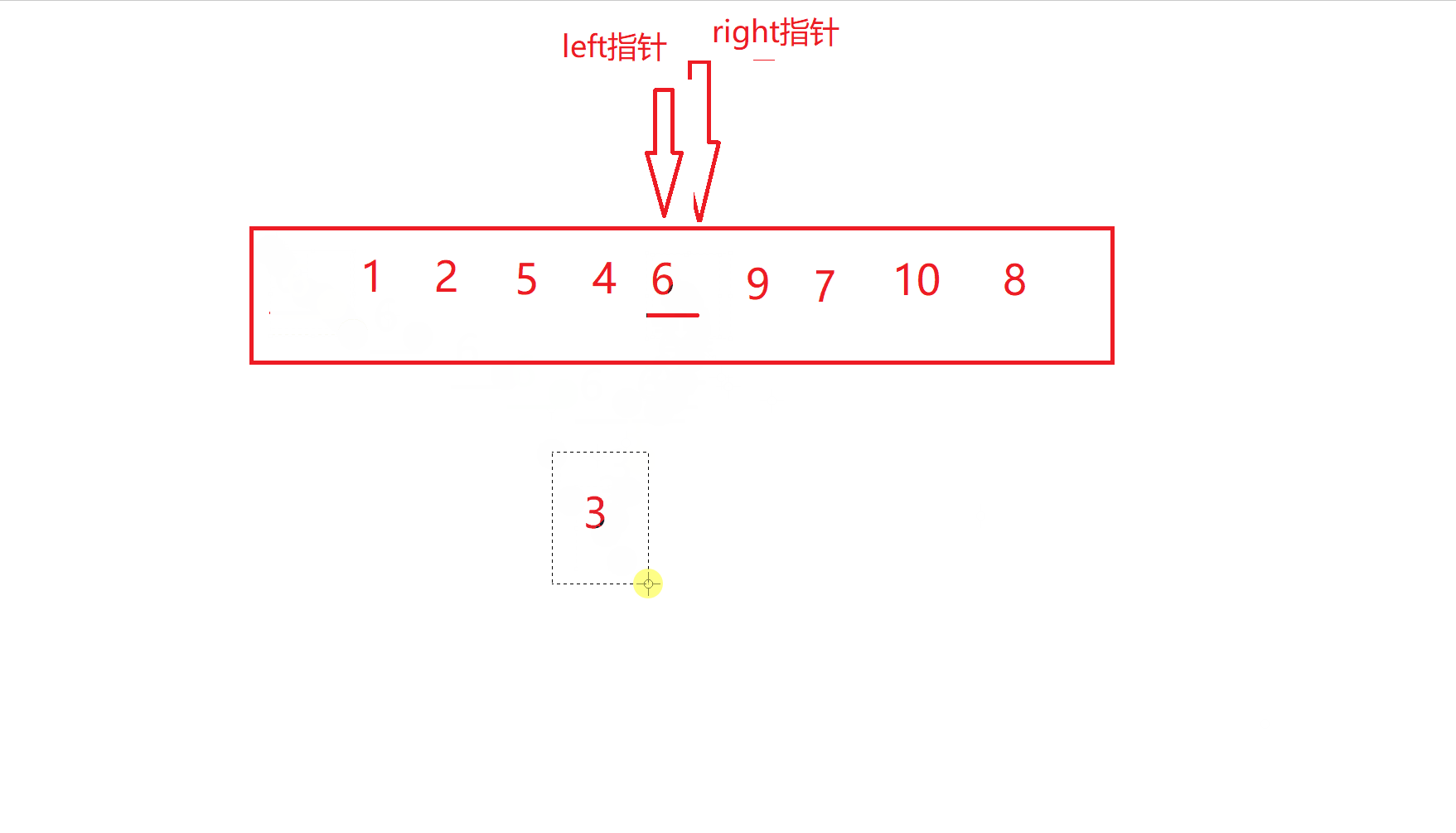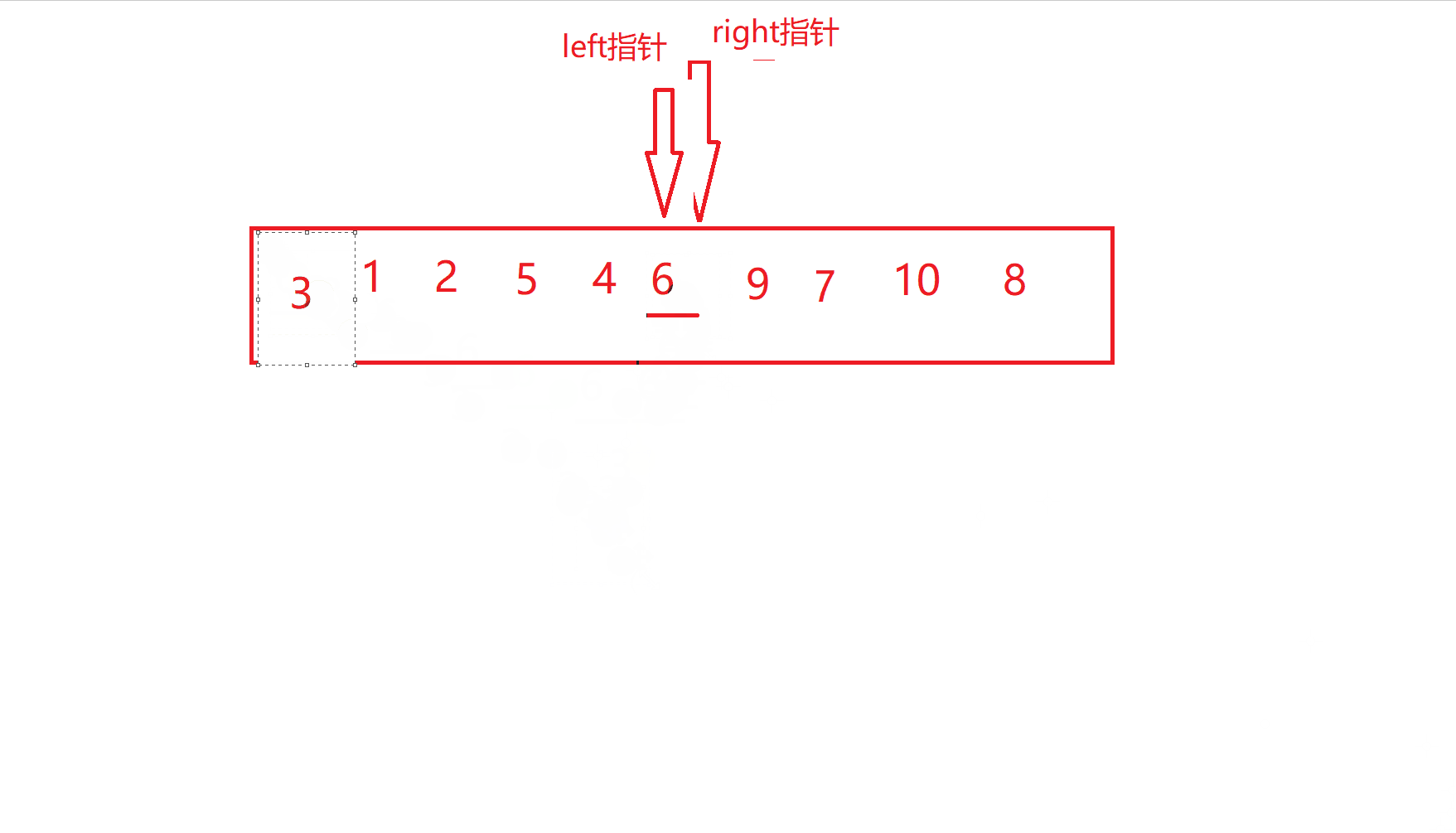
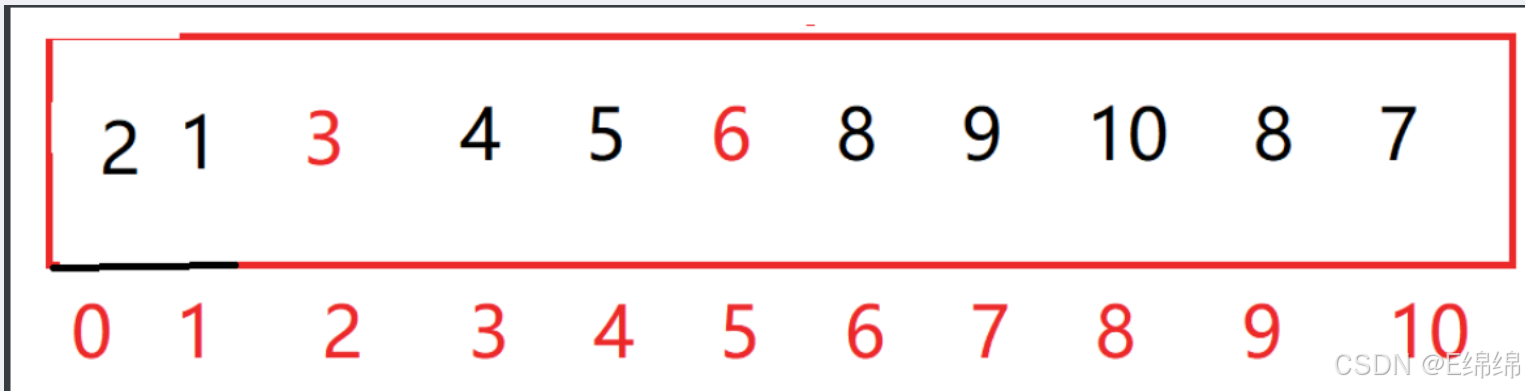
hoare版本的核心思路通俗来讲就是选取待排数组范围内的一个数作为关键字(一般是最左边或者最右边)将其放到他在有序数组中的位置上,也就是他本来应该在的位置,并且此时关键字的左边一定都是比关键字小的数,右边一定是比关键字大的数,然后再以此类推,直到所有的数都做为关键字放在了正确的位置上
可能用文字描述没那么直观,那么我们就用图去表示。
left和right停下之后就进行交换
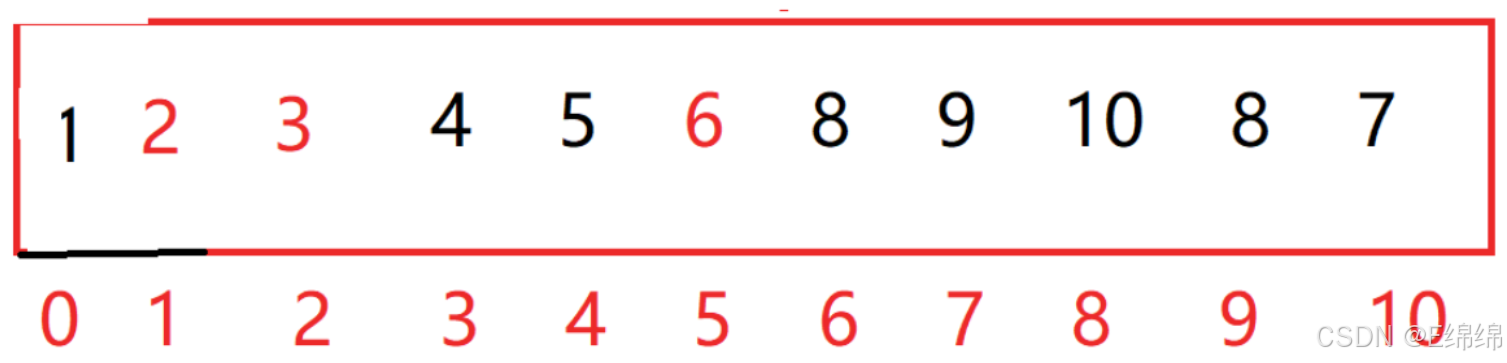
重复上述过程
当到达这一步时
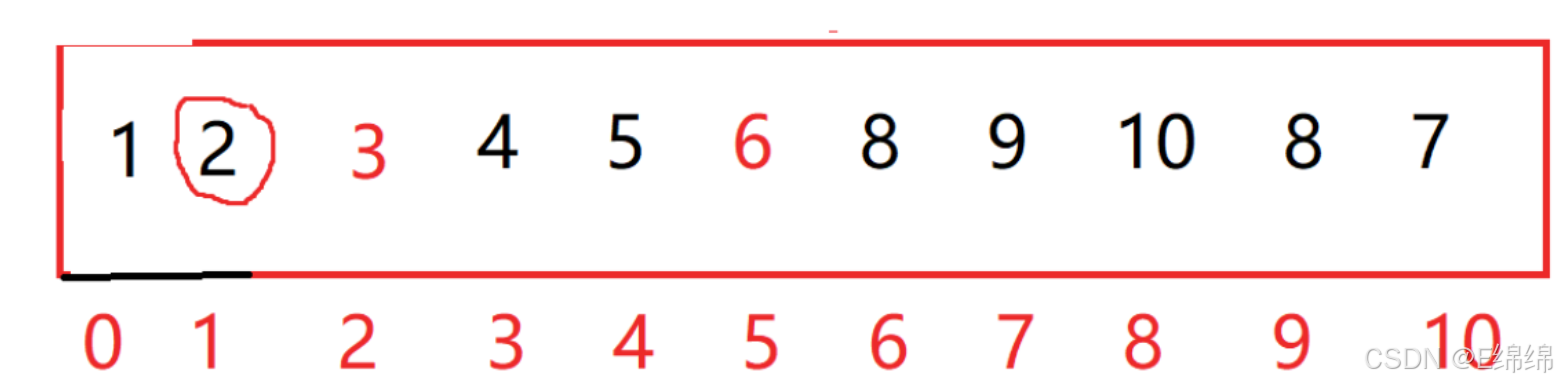
也就是left指针与right指针相遇了,此时交换关键字key和相遇位置的值
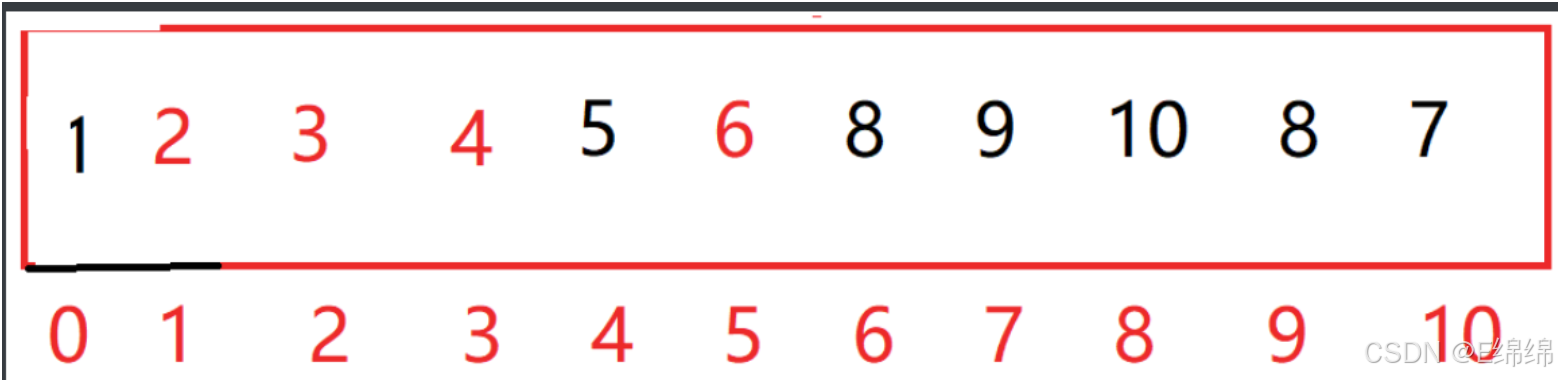
到这一步时,大家有没有发现,6的左边已经都是小于6的数,而右边都是大于6的数
现在解释一下为什么最左边做key时最右边要先走:
我们知道,left指针是去找大于key的数,因此停下来的位置的值一定比key大,若左边先出发,右边后出发且此时相遇了,那么相遇点的值一定是大于key的值,此时再交换,则达不到key的左右两边要么大要么小的目的。因此我们要保证提前相遇的位置与key交换后是想要的效果,若最左边做key,则右边先走,最右边做key则左边先走。
这样,我们快速排序的单趟排序就完成了,接下来只需不断改变左右区间,使得每个数字都落到正确的位置上,直到key的左右序列排序就完成啦,我们要记住一个结论,那就是数据只有一个时,便是有序的。
所以其单趟排序hoare版本代码如下:
public static int checkSort(int[] arr,int l,int r){ int key=arr[l]; int left=l+1; int right=r; while(left<=right){ while (arr[right]<=key&&left<=right) right--; while (arr[left]>key&&left<right) left++; if(left>=right) { swap(arr,right,l); return right; } else swap(arr,left,right); } return right; }既然我们的单趟排序完成了,那么对于如何完整的实现它,我们有两种思路:非递归和递归。
递归实现
//快速排序 从大往小 hoare版本 递归 public class Sort6 { public static void main(String[] args) { int[] arr = new int[10]; Random random = new Random(); for (int i = 0; i < 10; i++) { arr[i] = random.nextInt(100); } System.out.println(Arrays.toString(arr)); shell(arr,0,arr.length-1); System.out.println(Arrays.toString(arr)); } public static void shell(int[] arr,int l,int r) { if(l>=r) return; int mid = checkSort(arr,l,r); shell(arr,l,mid-1); shell(arr,mid+1,r); } public static int checkSort(int[] arr,int l,int r){ int key=arr[l]; int left=l+1; int right=r; while(left<=right){ while (arr[right]<=key&&left<=right) right--; while (arr[left]>key&&left<right) left++; if(left>=right) { swap(arr,right,l); return right; } else swap(arr,left,right); } return right; } public static void swap(int[] arr,int a,int b) { int temp=arr[a]; arr[a]=arr[b]; arr[b]=temp; } }
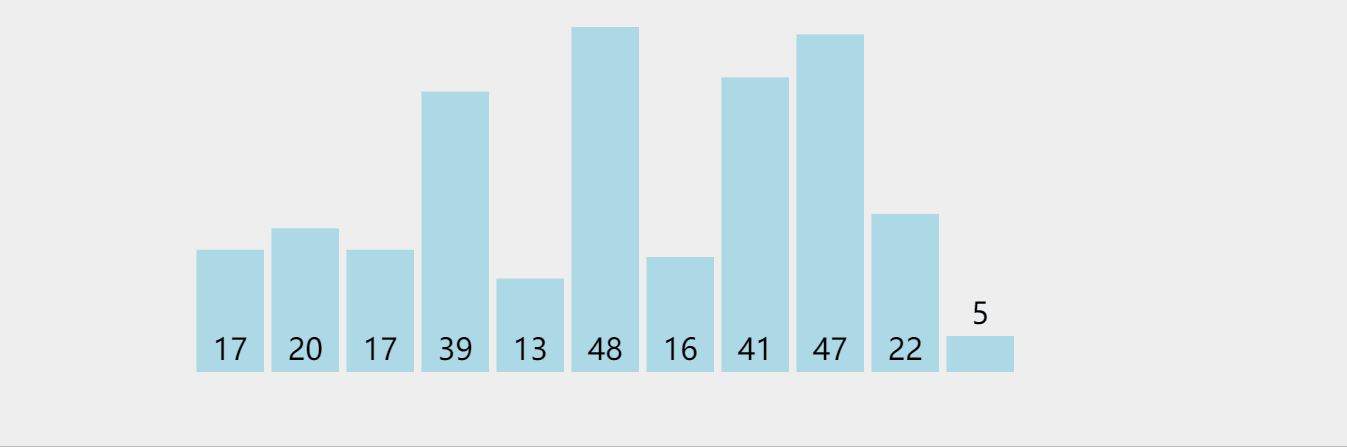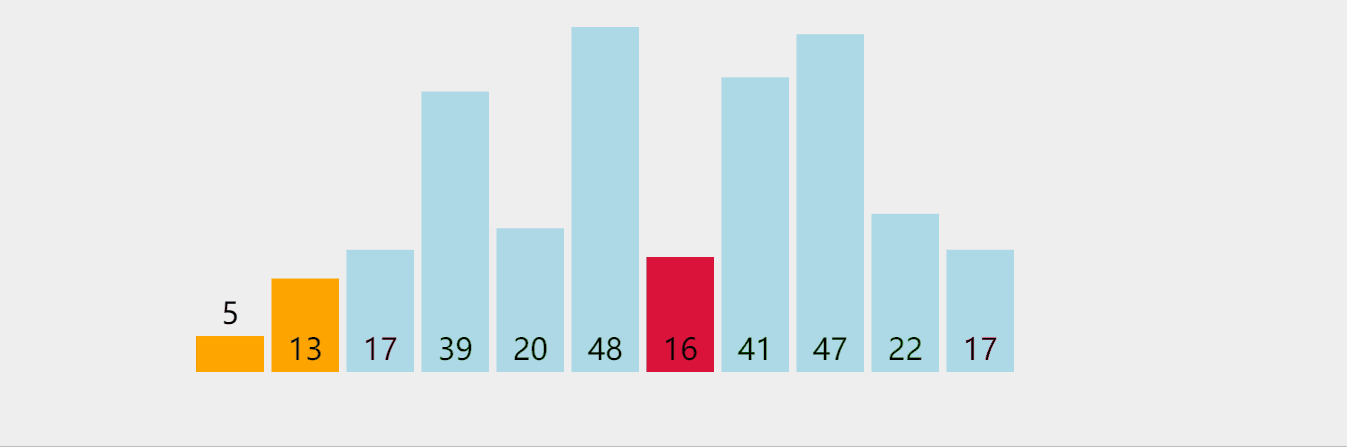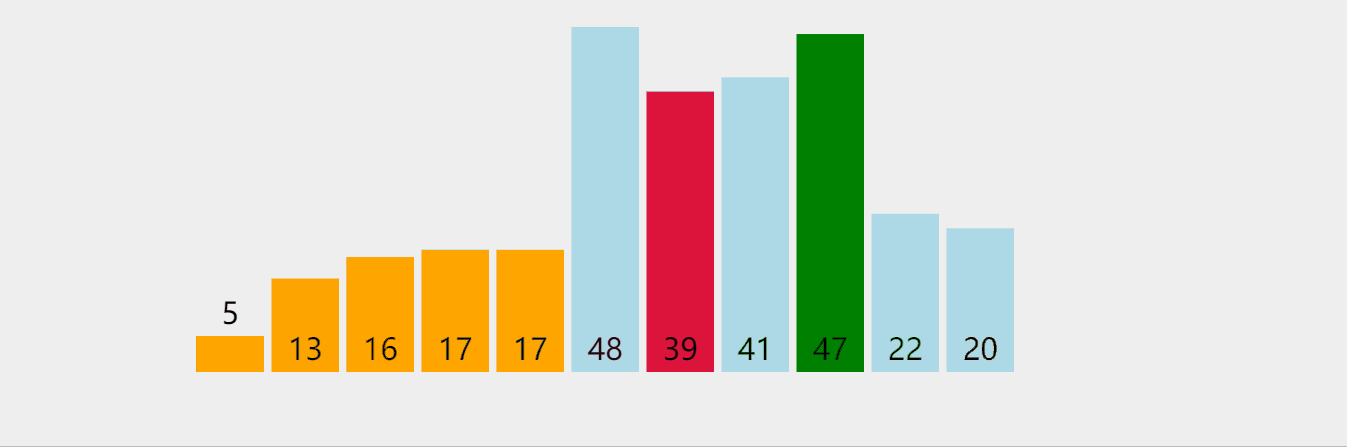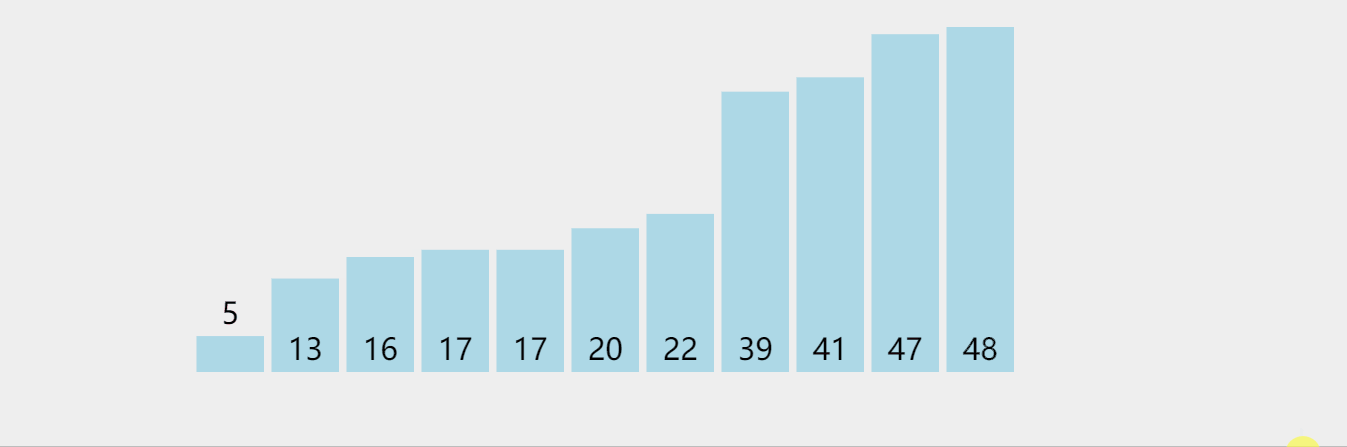
为了便于理解,我们拿刚才单趟排序后的这个序列继续进行排序。

经过上轮筛选,返回keyi=5
更新范围为[0,4],返回keyi=2——数值6的左边
更新范围为[0,1],返回keyi=0——数值3的左边
更新范围为[0,0],达到返回条件(默认有序)返回上层函数——数值2的左边
更新范围[1,1],达到返回条件,返回上层函数——数值2的右边
此层函数调用完成,返回上层函数
更新范围[3,4],返回keyi=3——数值3的右边
更新范围[3,3]——数值4的左边,更新范围[4,4]——数值4的右边,此层调用结束,一直返回到进入数值6的右边
此时左边已经有序了,而到后面也就是右边的排序就不再做解释,依旧保持着该规律。
非递归实现
由于栈的特点便是先进后出,后进先出,非常符合快速排序,所以非递归实现是由栈完成的。这里我们直接上代码,就不多说了,大家好好看代码理解一下思路。
//快速排序 从大往小 hoare版本 非递归 public class Sort7 { public static void main(String[] args) { int[] arr = new int[10]; Random random = new Random(); for (int i = 0; i < 10; i++) { arr[i] = random.nextInt(100); } System.out.println(Arrays.toString(arr)); shell(arr,0,arr.length-1); System.out.println(Arrays.toString(arr)); } public static void shell(int[] arr,int l,int r) { Stack<Integer> stack=new Stack<>(); int start=l; int end=r; int mid=checkSort(arr,start,end); if(mid>start+1) { stack.push(start); stack.push(mid-1); }if(mid<end-1) { stack.push(mid+1); stack.push(end); } while(!stack.isEmpty()){ end=stack.pop(); start=stack.pop(); mid= checkSort(arr,start,end); if(mid>start+1) { stack.push(start); stack.push(mid-1); }if(mid<end-1) { stack.push(mid+1); stack.push(end); } } } public static int checkSort(int[] arr,int l,int r){ int key=arr[l]; int left=l+1; int right=r; while(left<=right){ while (arr[right]<=key&&left<=right) right--; while (arr[left]>key&&left<right) left++; if(left>=right) { swap(arr,right,l); return right; } else swap(arr,left,right); } return right; } public static void swap(int[] arr,int a,int b) { int temp=arr[a]; arr[a]=arr[b]; arr[b]=temp; } }
单趟排序其他版本(挖坑法+前后指针法)
除了Hoare版本,我们还可以用挖坑法或前后指针法进行排序。
对于我们来说,其实这种单趟排序版本只要了解其中一个就行了,就我而言知道一个Hoare就ok,对于挖坑法和前后指针法了解一下就行了。
这里我就不多叙述了,我们看下这篇文章,里面有详细阐述: 超详细八大排序+基数排序
快速排序的两大优化
快速排序顾名思义,排序速度听着就很快,时间复杂度最好情况为O(N*logN)
但若遇到这两种特殊情况——数组原本就有序或者数组内数据全部一样,时间复杂度会上升到O(N^2)。
我们都知道,在内存中,栈的空间只有4兆左右,因此面对那两种特殊情况,对于递归的方法来说,递归调用的次数太多,栈溢出的可能性非常之大,因此,除了用非递归的方法解决栈溢出的问题之外,前辈们还提出了两种优化递归方法的思路——小区间优化和三数取中
小区间优化:
考虑到快排越到后面时,小区间的递归次数越多,我们可以采用与其他排序法相结合的方式来减小递归次数。所以对于区间内已经接近有序且区间范围小,我们选用插入排序来优化小区间,这样子效率更高。
三数取中:
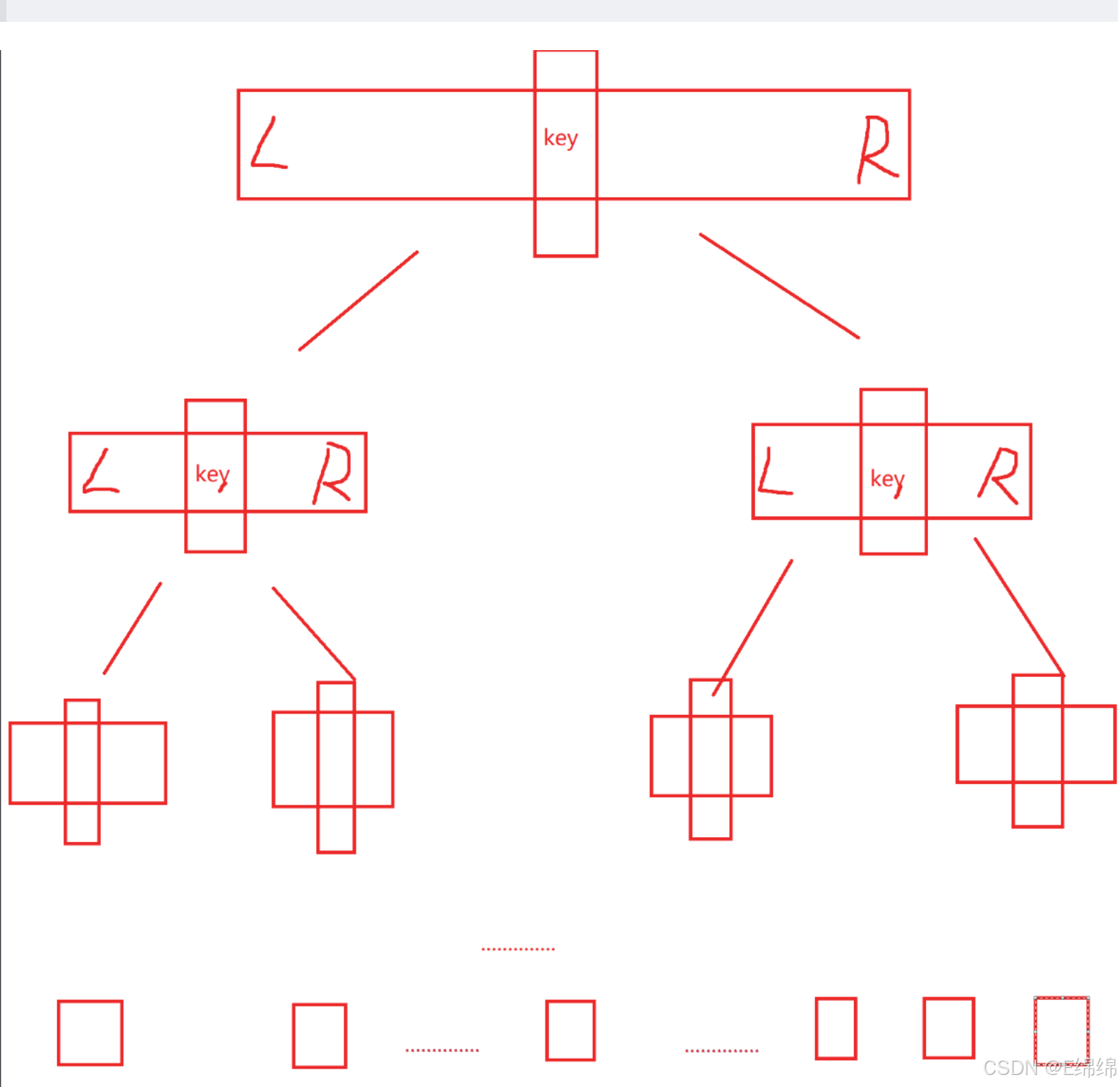
一般地,我们都选用最左边的数值当key,因为我们只考虑了数组是无序的情况,也就是key很大程度上正确位置是处在中间部分,如下图
这种情况是快排的理想情况,类似于二叉树的结构,将快排的时间复杂度控制在了o(N*logN)
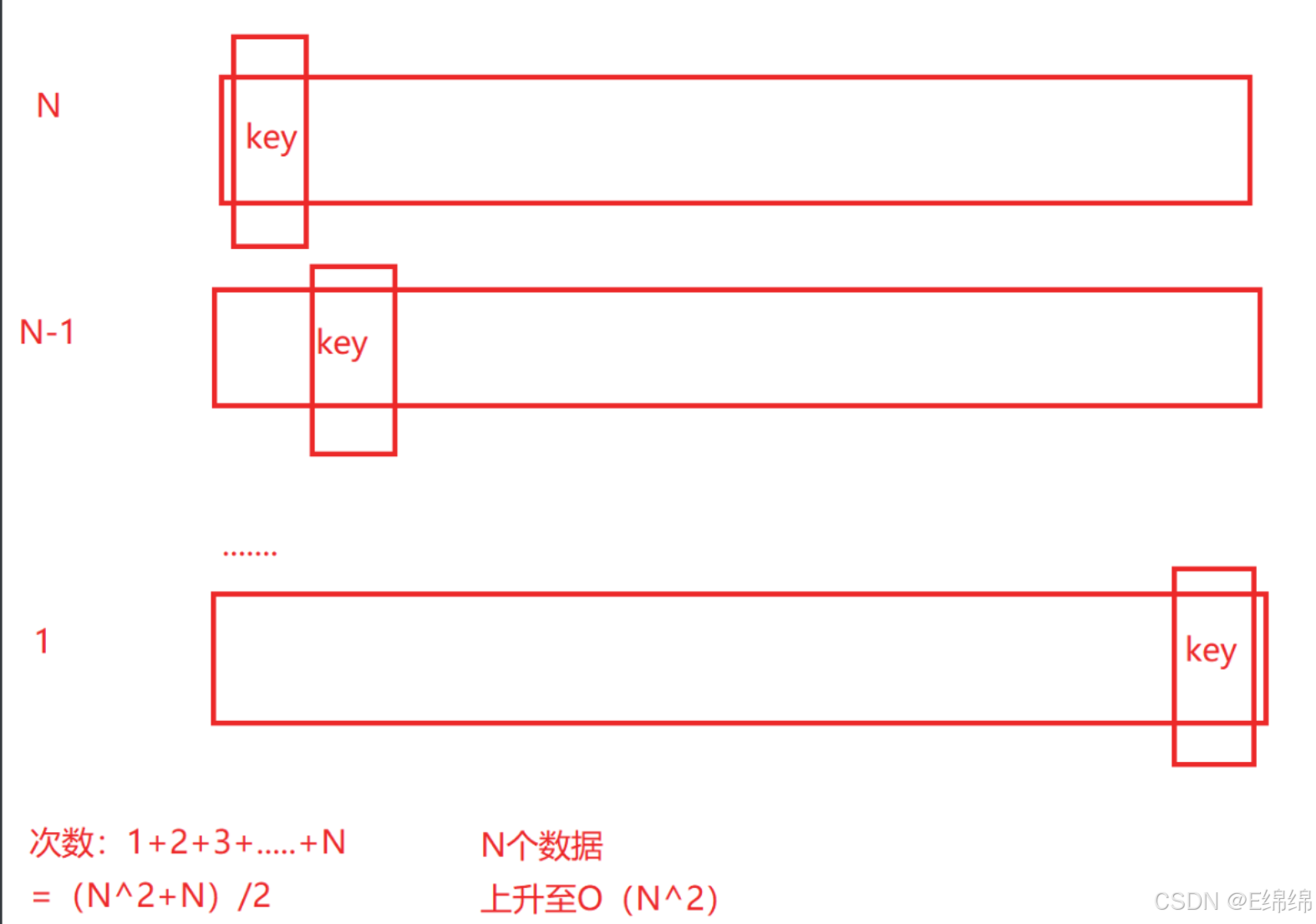
但倘若此时数组已有序,或者数组内都是一样的内容,那效果可大不相同.
为了优化这种极端情况,我们采用三数取中法,使得选中的key大机率上的正确位置在中间.
方法:在数组的最左,中间,最右选取中间大小的数,将其再跟最左边的数交换一下,从而将最坏情况下的快排优化到接近最好。
代码如下:
public class Sort6 { public static void main(String[] args) { int[] arr = new int[10]; Random random = new Random(); for (int i = 0; i < 10; i++) { arr[i] = random.nextInt(100); } System.out.println(Arrays.toString(arr)); shell(arr,0,arr.length-1); System.out.println(Arrays.toString(arr)); } public static void shell(int[] arr,int l,int r) { if(l>=r) return; int mid = checkSort(arr,l,r); shell(arr,l,mid-1); shell(arr,mid+1,r); } public static int checkSort(int[] arr,int l,int r){ int m= GetMiddle(arr,l,r); swap(arr,m,l); int key=arr[l]; int left=l+1; int right=r; while(left<=right){ while (arr[right]<=key&&left<=right) right--; while (arr[left]>key&&left<right) left++; if(left>=right) { swap(arr,right,l); return right; } else swap(arr,left,right); } return right; } public static void swap(int[] arr,int a,int b) { int temp=arr[a]; arr[a]=arr[b]; arr[b]=temp; } public static int GetMiddle(int[] a, int left, int right) { int mid = left + (right - left)/2; if (a[left] > a[mid]) { if (a[mid] > a[right]) return mid; else if (a[left] < a[right]) return left; else return right; } else { if (a[mid] < a[right]) return mid; else if (a[left] > a[right]) return left; else return right; } } }
3.7 归并排序
基本思路
归并排序是利用归并的思想实现的排序方法,该算法采用经典的分治策略:分将问题分成一些小的问题然后递归求解,而治的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之。
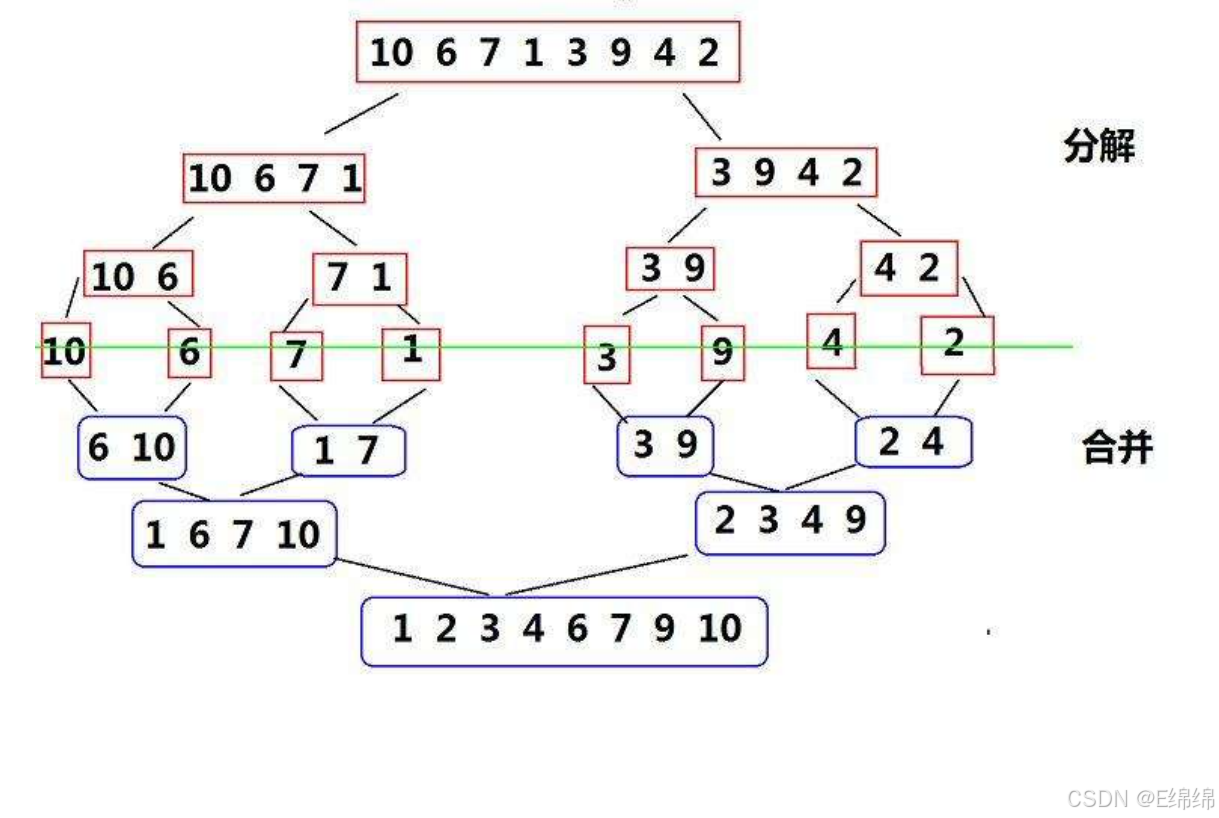
我们先用一张动图演示全过程,再分解过程。
这个过程现在看不懂没关系,我们一步一步来分析
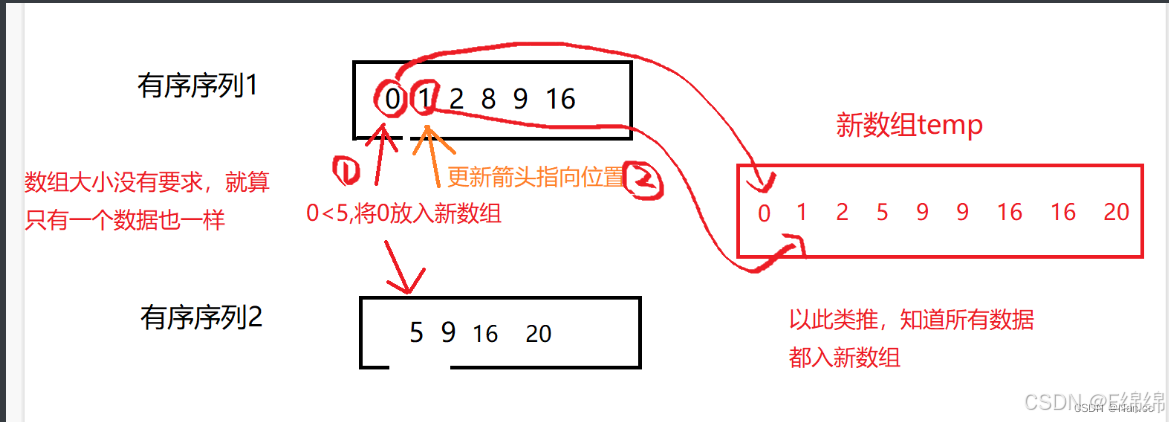
假如现在有两个有序序列让你排序,应该自然会想到合并两个有序子序列,也就是新开辟一块空间,并依次比较分别比较两个子序列的大小然后放入新空间中,如下图
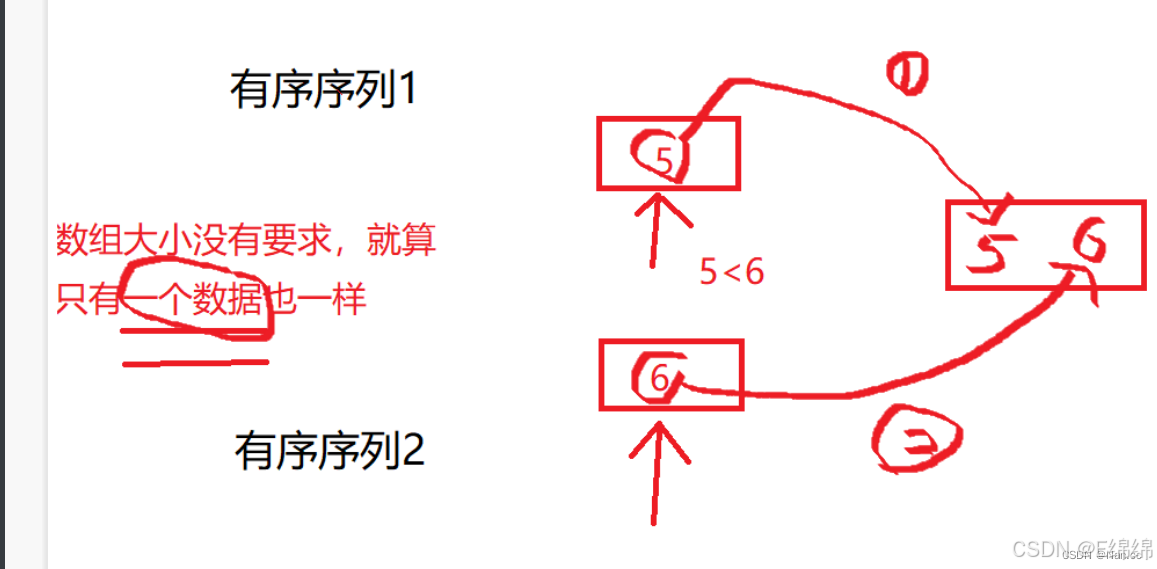
有了这样一个思路,我们就要有以合并两个有序序列从而得到一个新的有序序列为目的的思想,也就是说,给你一个完全无序的数组,我们才用分而治之的方法,将一个无序数组变成两个有序数组,再变回一个有序数组,那么就有的同学会问了,要是数组一直是无序怎么办呢?但如果是下面这种情况,是否会让你恍然大悟?
现在来细品只有一个数据,是否就很清晰呢,是的,一个数据,就是一个有序数组!
于是,我们就有了下面这张图:
这样我们的思路就显而易见:给定一个无序数组,我们将其不断划分左右区间,知道区间内只有一个数据时,我们开始合并两个有序数组,层层递进,直到全部有序,想要达成目的,我们有两种思路来解决:
递归思想
非递归思想
递归实现
这里直接上代码
//归并排序 从大往小 递归 public class Sort8 { public static void main(String[] args) { int[] arr = new int[10]; Random random = new Random(); for (int i = 0; i < 10; i++) { arr[i] = random.nextInt(100); } System.out.println(Arrays.toString(arr)); shell(arr, 0, arr.length - 1); System.out.println(Arrays.toString(arr)); } public static void shell(int[] arr, int l, int r) { //返回条件:只有一个数据 if(l>=r) return; int mid=(l+r)/2; //先递归左序列,后递归右序列,划分左右区间 shell(arr,l,mid); shell(arr,mid+1,r); partSort(arr,l,r,mid);//将其合并变为有序 } public static void partSort(int[] arr1, int l, int r,int mid) { int first1=l; int end1=mid; int first2=mid+1; int end2=r; int[] arr2=new int[r-l+1]; int i=0; while(first1<=end1&&first2<=end2) { if(arr1[first1]>=arr1[first2]) { arr2[i]=arr1[first1]; first1++; } else { arr2[i] = arr1[first2]; first2++; } i++; } while (first1<=end1){ arr2[i]=arr1[first1]; first1++; i++; } while (first2<=end2){ arr2[i]=arr1[first2]; first2++; i++; } for (int j = 0; j <arr2.length ; j++) { arr1[l+j]= arr2[j]; } } public static void swap(int[] arr,int a,int b) { int temp=arr[a]; arr[a]=arr[b]; arr[b]=temp; } }若递归的思路不好理解的话,大家可以拿纸一步一步跟着代码思路走,下面我给一张图做理解参考。
时间复杂度:O(N*logN)空间复杂度:O(N)
非递归实现
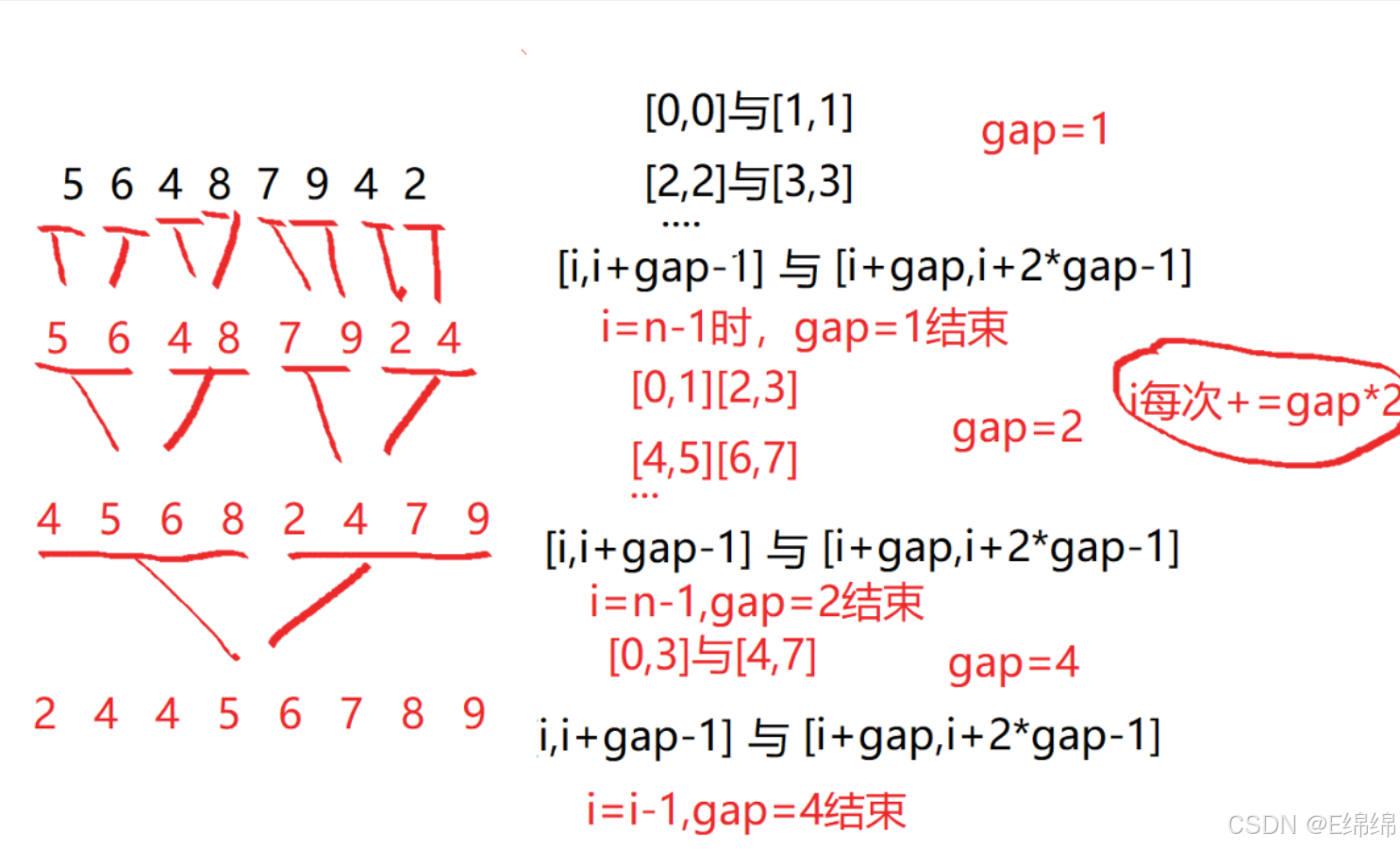
递归搞明白了,非递归其实也一样,无非就是控制合并两个有序数组时数组的范围从小到大一步一步变成有序
我们用下图来理解
以上例子举的是数组元素恰好是2的3次方个个数,若数组不为2的幂关系,则除了最开头的一定<n不会越界之外,其他的比如中间或者最后都很容易会越界,因此我们要进行一定的边界控制。 如下:
所以整体代码如下:
//从大到小 public class Sort9 { public static void main(String[] args) { int[] arr = new int[10]; Random random = new Random(); for (int i = 0; i < 10; i++) { arr[i] = random.nextInt(100); } System.out.println(Arrays.toString(arr)); shell(arr, 0, arr.length - 1); System.out.println(Arrays.toString(arr)); } public static void shell(int[] arr1, int l, int r) { int gap=1; while (gap<arr1.length) { for (int j = 0; j < arr1.length ; j = j + 2 * gap) { int first1 = j; int mid = j + gap - 1; if (mid >= arr1.length) { mid = arr1.length - 1; } int end2 = mid + gap; if (end2 >= arr1.length) { end2 = arr1.length - 1; } int first2 = mid + 1; int end1 = mid; int[] arr2 = new int[end2 - first1 + 1]; int i = 0; while (first1 <= end1 && first2 <= end2) { if (arr1[first1] >= arr1[first2]) { arr2[i] = arr1[first1]; first1++; } else { arr2[i] = arr1[first2]; first2++; } i++; } while (first1 <= end1) { arr2[i] = arr1[first1]; first1++; i++; } while (first2 <= end2) { arr2[i] = arr1[first2]; first2++; i++; } for (int k = 0; k <arr2.length ; k++) { arr1[j+k]= arr2[k]; } } gap*=2; } } }如果这非递归思路看起来不好理解的话,大家可以拿纸跟着这个代码一步一步去走,这样就比较容易理解了。
4.计数排序
计数排序是一种非比较排序,其核心是将序列中的元素作为键存储在额外的数组空间中,而该元素的个数作为值存储在数组空间中,通过遍历该数组排序。
下面我们直接看图:
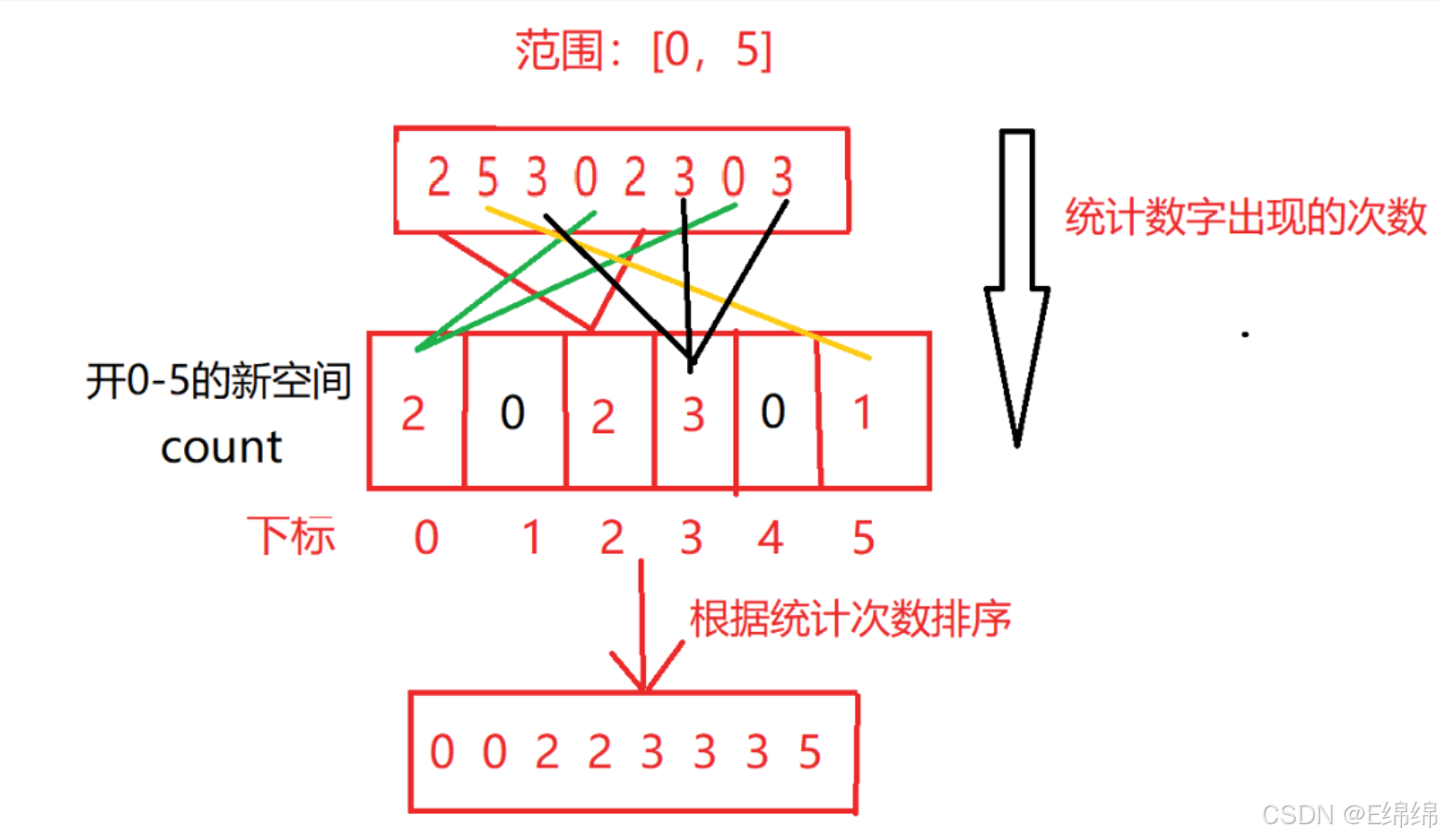
所以其整体代码如下
//从大到小 public class Sort10 { public static void main(String[] args) { int[] arr = new int[10]; Random random = new Random(); for (int i = 0; i < 10; i++) { arr[i] = random.nextInt(100); } System.out.println(Arrays.toString(arr)); shell(arr); System.out.println(Arrays.toString(arr)); } public static void shell(int[] arr1 ) { int max=arr1[0]; int min=arr1[0]; for (int i = 1; i < arr1.length ; i++) { if(arr1[i]>max){ max=arr1[i]; } if(arr1[i]<min){ min=arr1[i]; } } int[] arr=new int[max-min+1]; for (int i = 0; i <arr1.length ; i++) { arr[arr1[i]-min]++; } int j=0; for (int i = arr.length-1; i >=0 ; i--) { while(arr[i]>0){ arr1[j]=i+min; j++; arr[i]--; } } } }
但由这代码我们也可以发现有一个很大的缺点:
待排序列中最大值与最小值差距不能过大,由于是根据范围开辟新空间,因此很容易很容易造成内存浪费。
5.基数排序+桶排序
这里我们详细讲了计数排序后就不再详细讲基数排序和桶排序了。
这里我直接上这两个排序相关的链接,大家可以看一下,里面有详细描述且有详细代码。
6.总结
所以这里我们的排序篇章就讲完了,下篇文章将会给大家带来Map和Set的讲解。在此,我们诚挚地邀请各位大佬们为我们点赞、关注,并在评论区留下您宝贵的意见与建议。让我们共同学习,共同进步,为知识的海洋增添更多宝贵的财富!🎉🎉🎉❤️❤️💕💕🥳👏👏👏