列表在 GeoGebra 中扮演着重要角色,使用户能够处理和管理一组数值、点或对象。这些列表可以用于执行多种操作,如计算平均值、排序、查找最大或最小值、绘制点的集合等。通过使用列表,用户可以简化复杂的计算步骤,增强图形的动态性和互动性。本文将介绍如何在 GeoGebra 中创建和操作列表,展示列表在数学教学、数据分析和几何构建中的实际应用。通过掌握这些列表操作技巧,您可以进一步提升 GeoGebra 的使用效果,创造更加丰富和生动的数学模型。
目录
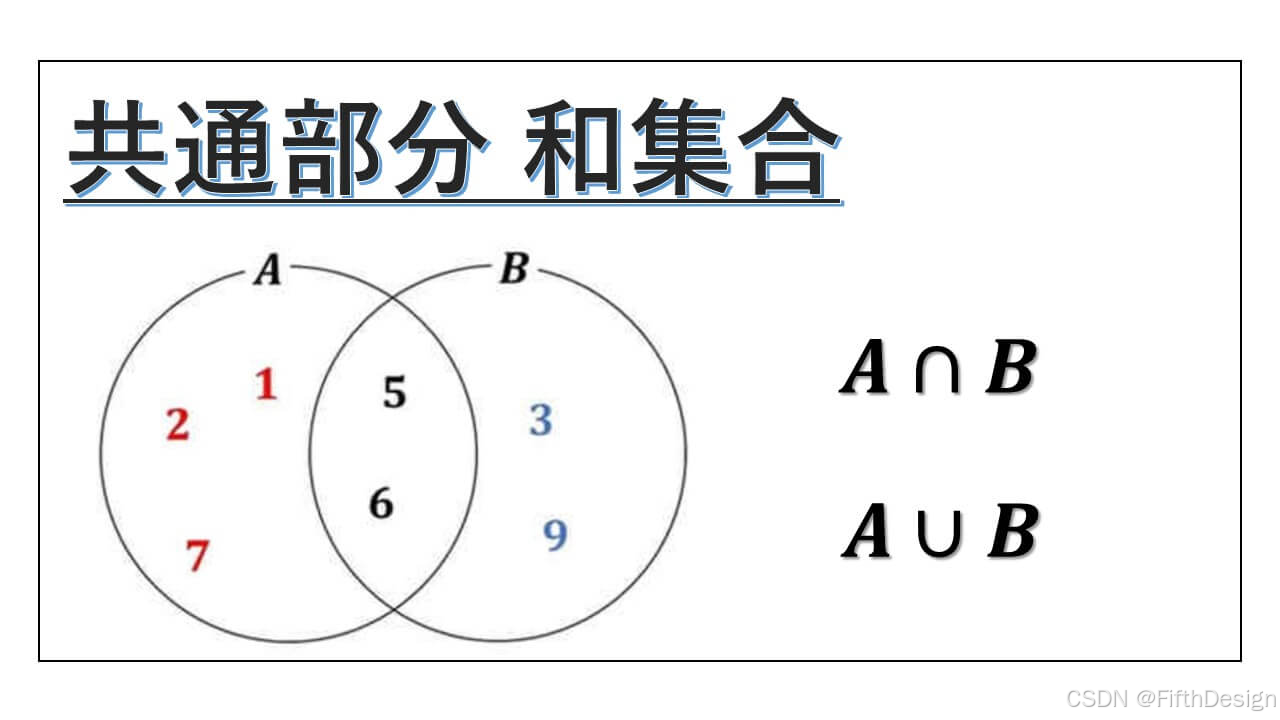
一、关于列表与集合
1. 列表与集合的对比
老实说,我第一次接触到GeoGebra的列表时有些懵,我们先来看一下GeoGebra中列表与集合的对比:
| 特性 | 列表 (List) | 集合 (Set) |
|---|---|---|
| 创建方式 | 使用 {} 创建 | 使用 {} 创建并确保元素唯一 |
| 元素顺序 | 有序 | 无序 |
| 元素重复 | 允许重复 | 不允许重复 |
| 访问方式 | 通过索引访问(从1开始) | 不能通过索引访问 |
| 示例 | {1, 2, 2, 3, 4, 5} | {1, 2, 3} |
| 并集运算 | 不支持直接运算 | 支持直接运算 (∪) |
| 交集运算 | 不支持直接运算 | 支持直接运算 (∩) |
| 差集运算 | 不支持直接运算 | 支持直接运算 (\) |
| 使用场景 | 数据分析、绘图、统计计算 | 集合运算、逻辑判断 |
| 转换为集合 | Set[List] | 不需要转换,直接使用 |
| 示例操作 | Element[List, 2] 返回第2个元素 | Union = Set1 ∪ Set2 计算并集 |
如果说C语言是万剑之宗,那么衍生出来的GeoGebra这把剑一定是个另类,因为有几个奇怪的地方:
- GeoGebra列表有序、且可以重复,但从1开始索引;
- GeoGebra列表与集合的创建方式一样;
- {1,2,3}默认是列表,除非上文中有交、并、差运算,系统才确定它是集合;
- 列表可以转换为集合,用的是
Set[List]
2. 列表转集合
因为集合是不重复的,所以可以利用这个原理进行列表的去重。
// 定义列表 L = {1, 2, 2, 3, 4, 5, 5} // 将列表转换为集合 SetL = Set[L] // 输出结果 SetL // 结果为 {1, 2, 3, 4, 5} 3. 集合转列表
注意,集合是无需的,元素是不重复的,列表是有序的,元素可以重复(数学中的理论)
// 定义集合 Set1 = {5, 2, 8, 1} // 将集合转换为列表 ListFromSet = Sequence(Element[Set1, i], i, 1, Length[Set1]) // 输出结果 ListFromSet // 结果为 {5, 2, 8, 1} // 对列表进行排序(可选) SortedList = Sort[ListFromSet] // 输出排序后的列表 SortedList // 结果为 {1, 2, 5, 8} 二、列表的操作
1. 列表-创建
(1)直接创建法:直接在命令行输入下边命令,就可以创建列表(注意,花括号默认创建列表,列表进行交集、并集处理后会自动转成集合)。
L = {1, 2, 3, 4, 5} (2)使用序列法:
这将创建一个名为L的列表,包含从1到10的平方数:{1, 4, 9, 16, 25, 36, 49, 64, 81, 100}
L = Sequence(n^2, n, 1, 10) 
2. 列表-新增元素
可以使用GeoGebra的Append命令向列表中添加元素(和Python的关键字一样):
L = {1, 2, 3} Append(L, 4) // L现在变为{1, 2, 3, 4} 3. 列表-删除元素
使用Remove命令可以删除指定位置的元素:
L = {1, 2, 3, 4, 5} Remove(L, 3) // L现在变为{1, 2, 4, 5} 4. 列表-访问元素
可以使用方括号语法访问列表中的特定元素(程序员请注意,这里是从1开始):
L = {10, 20, 30, 40, 50} L(3) // 返回30 5. 列表-修改元素
通过重新定义列表中的特定位置元素,可以修改列表:
L = {10, 20, 30, 40, 50} SetValue(L, 3, 35) // 将第3个元素改为35,现在L为{10, 20, 35, 40, 50} 6. 列表-遍历列表
可以使用Sequence命令或循环来遍历列表中的元素。例如,计算列表中所有元素的平方并存储在新列表中:
L = {1, 2, 3, 4, 5} SquaredList = Sequence(Element(L, i)^2, i, 1, Length(L)) // SquaredList为{1, 4, 9, 16, 25} 7. 列表-合并列表
你可以使用Join命令合并两个或多个列表:(注意,这个操作后仍是列表,元素可以重复)
L1 = {1, 2, 3} L2 = {3, 4, 5} L = Join(L1, L2) // L为{1, 2, 3, 3, 4, 5} 7. 列表-获取列表长度
L = {1, 2, 3, 4, 5} Length(L) // 返回5 8. 列表-查找元素索引:
L = {10, 20, 30, 40, 50} IndexOf(L, 30) // 返回3 9. 列表-列表求和::
L = {1, 2, 3, 4, 5} Sum(L) // 返回15 10. 列表-列表排序:
L = {5, 2, 8, 1, 4} Sort(L) // 返回{1, 2, 4, 5, 8} 11. 列表-反转列表:
L = {1, 2, 3, 4, 5} Reverse(L) // 返回{5, 4, 3, 2, 1} 三、集合的操作
1. 集合-创建(与列表一致):
(1)直接创建法:直接在命令行输入下边命令,就可以创建集合(注意,虽说花括号默认创建列表,但后续我们一旦对列表进行集合的操作,就会自动转换成集合)。
L = {1, 2, 3, 4, 5} (2)使用序列法:
这将创建一个名为L的集合,包含从1到10的平方数:{1, 4, 9, 16, 25, 36, 49, 64, 81, 100}
L = Sequence(n^2, n, 1, 10) 
2. 集合-新增元素:
集合中的元素是唯一的,添加重复元素不会改变集合:
S = {1, 2, 3} S = Union(S, {4}) // S现在变为{1, 2, 3, 4} S = Union(S, {3}) // S仍然是{1, 2, 3, 4},因为3已经在集合中 3. 集合-删除元素:
使用Difference命令可以从集合中删除元素:
S = {1, 2, 3, 4, 5} S = Difference(S, {3}) // S现在变为{1, 2, 4, 5} 4. 集合-访问元素:
集合没有固定的顺序,因此不能通过索引访问特定元素。但是可以使用Element命令访问集合中的元素:
S = {10, 20, 30, 40, 50} Element(S, 3) // 返回集合中的第三个元素 5. 集合的并集:
使用Union命令可以求两个集合的并集:
S1 = {1, 2, 3} S2 = {3, 4, 5} S = Union(S1, S2) // S为{1, 2, 3, 4, 5} 6. 集合的交集:
使用Intersection命令可以求两个集合的交集:
S1 = {1, 2, 3} S2 = {3, 4, 5} S = Intersection(S1, S2) // S为{3} 7. 集合的差集:
使用Intersection命令可以求两个集合的交集:
S1 = {1, 2, 3} S2 = {3, 4, 5} S = Difference(S1, S2) // S为{1, 2} 8. 集合的补集:
假设有一个全集U,使用Complement命令可以求集合的补集:
U = {1, 2, 3, 4, 5} S = {2, 4} C = Complement(U, S) // C为{1, 3, 5} 9. 集合的子集:
使用Subset命令可以获取集合的子集:
S = {1, 2, 3, 4, 5} Subsets(S, 2) // 返回{ {1, 2}, {1, 3}, {1, 4}, {1, 5}, {2, 3}, {2, 4}, {2, 5}, {3, 4}, {3, 5}, {4, 5} } 10. 集合-判断元素是否在集合中:
S = {1, 2, 3, 4, 5} Contains(S, 3) // 返回true 11. 集合-获取集合大小:
S = {1, 2, 3, 4, 5} Size(S) // 返回5 12. 集合-求集合的幂集:
S = {1, 2, 3} PowerSet(S) // 返回{ {}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3} } 13. 集合-判断集合是否为空:
S = {} IsEmpty(S) // 返回true 四、文章最后
如有需要随时联系,当然,随时欢迎技术咨询。
