非递归的归并排序

我们之前讲的快速排序有非递归的写法，那么归并排序也有非递归写法，我们一起来研究一下吧。

快速排序的非递归算法是使用的手动搭栈的方法，将区间存入栈里面，然后再排序，但是这次的归并排序可以吗？大家都知道归并排序是让左区间有序，右区间有序，然后再回到原来的区间使其有序，这个思路就类似于我们之前了解的后序一样，而快速排序就类似于中序，所以说，这次的归并排序就不能用搭栈的方法来实现非递归，那么，我们怎么实现呢？

思路，我们让这个数组先每个数一组，然后，使每一组都有序，然后，使每两组都有序，以此类推，我们就可以让整个数组有序。废话少说，大家看图：

相信我画的这幅图应该很清楚的表述了我的思路。

细节处理 

以上是大的思路，但是我们也有很多小细节也要处理好，否则千里之堤溃于蚁穴，前功尽弃。

区间处理

如上图所示，我们每次都会先分成两组，然后让他们有序，最好的方法就是设置两个区间，然后，再用变量控制这个区间，这是效率最高，又通俗易懂的方法，那么两个区间就是 

【begin1   end1】，【begin2   end2】；

设置一个i变量控制我们最左区间，设置一个gap等于我们每一组的数据个数，具体对应的样子上面的图也展示的很清楚，begin1就是i，然后其余的数就是根据这个gap来确定的，具体是什么样子请看下图：

这样安排数组就可以达到滚车轮的效果。

单数数组的越界 

我们先看一张图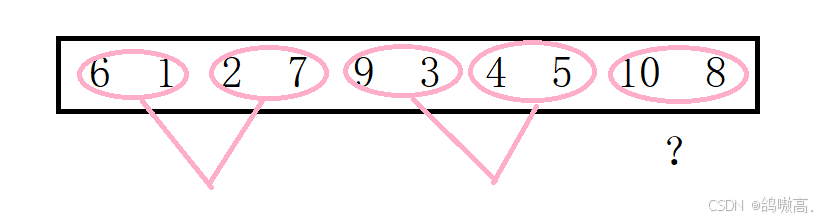

这就很准确的表达了我们遇到的问题，万一给的数组不能双双配对怎么办？我们继续看后面 

上图是区间的变化图，显示的第一个越界是end2越界，第二个就是begin2和end2越界，所以说我们需要有针对这两种情况的处理办法，第一种，begin2和end2都越界，我们就抛弃他们，然后进入 下一个循环，第二种，end2越界，那么就让end2等于n-1。

代码展示

//非递归的归并排序 void MergeSortNonR(int* a, int* tmp,int n) { 	int gap = 1; 	while (gap < n) 	{ 		for (int i = 0; i < n;i += gap * 2) 		{ 			int begin1 = i; 			int end1 = i + gap - 1; 			int begin2 = i + gap; 			int end2 = i + gap * 2 - 1; 			if (begin2 >= n) 			{ 				break; 			} 			if (end2 >= n) 			{ 				end2 = n - 1; 			} 			int j = i;  			while (begin1 <= end1 && begin2 <= end2) 			{ 				if (a[begin1] < a[begin2]) 				{ 					tmp[j++] = a[begin1++]; 				} 				else 				{ 					tmp[j++] = a[begin2++]; 				} 			} 			//第一个数组没有全部进tmp数组 			while (begin1 <= end1) 			{ 				tmp[j++] = a[begin1++]; 			} 			//第二个没进 			while (begin2 <= end2) 			{ 				tmp[j++] = a[begin2++]; 			} 			memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));  		} 		gap = gap * 2;  	}  }

大家可以试着自己调试一下。