阅读量:0

文章目录
- 一、背景 P124 - 125
- 二、基本概念 P125 - 130
- 三、取样与取样函数的傅里叶变换 P131 - P137
- 四、单变量的离散傅里叶变换(DFT) P138 - P140
- 五、两个变量的函数的扩展 P141 - P147
- 六、二维离散傅里叶变换的一些性质 P148 - P159
- 本章知识点小结
一、背景 P124 - 125
- 傅里叶指出,任何周期函数都可以表示为不同频率的正弦和/或余弦之和的形式,每个正弦项和/或余弦项都乘以不同的系数(现在称为傅里叶级数)
- 对于非周期函数,也可以正弦和/或余弦乘以加权函数的积分来表示。在这种情况下的公式就是傅里叶变换
二、基本概念 P125 - 130
2.1 复数 P125 - P126
- 复数
C = R + j I C = R + jI C=R+jI - 极坐标表示复数
c = ∣ c ∣ ( c o s θ + j s i n θ ) c =\vert{c}\vert(cos\theta + jsin\theta) c=∣c∣(cosθ+jsinθ) - 欧拉公式
e j θ = c o s θ + s i n θ e^{j\theta} = cos\theta + sin\theta ejθ=cosθ+sinθ - 欧拉公式变换后的极坐标表示复数
c = ∣ c ∣ e j θ c =\vert{c}\vert e^{j\theta} c=∣c∣ejθ
2.2 傅里叶级数 P126
f ( t ) = ∑ n = − ∞ ∞ c n e j 2 π n T t f(t) = \displaystyle\sum_{n=-\infty}^\infty c_ne^{j\frac{2\pi n}{T}t} f(t)=n=−∞∑∞cnejT2πnt
式中,
c n = 1 T ∫ − T 2 T 2 f ( t ) e − j 2 π n T t d t , n = 0 , ± 1 , ± 2 , ± 3 c_n = \frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)e^{-j\frac{2\pi n}{T}t}dt,n = 0,\pm1,\pm2,\pm3 cn=T1∫−2T2Tf(t)e−jT2πntdt,n=0,±1,±2,±3
2.3 冲激及其取样特性 P126 - P128
- 连续函数的冲激取样
① δ ( t ) = { ∞ , t = 0 0 , t ≠ 0 \delta(t) = \begin{cases} \infty,t = 0\\ 0,t ≠ 0\\ \end{cases} δ(t)={ ∞,t=00,t=0
② ∫ − ∞ ∞ δ ( t ) d t = 1 \int_{-\infty}^{\infty}\delta(t)dt = 1 ∫−∞∞δ(t)dt=1
③ ∫ − ∞ ∞ f ( t ) δ ( t ) d t = f ( 0 ) \int_{-\infty}^{\infty}f(t)\delta(t)dt = f(0) ∫−∞∞f(t)δ(t)dt=f(0)
④ ∫ − ∞ ∞ f ( t ) δ ( t − t 0 ) d t = f ( t 0 ) \int_{-\infty}^{\infty}f(t)\delta(t - t_0)dt = f(t_0) ∫−∞∞f(t)δ(t−t0)dt=f(t0) - 离散函数的冲激取样
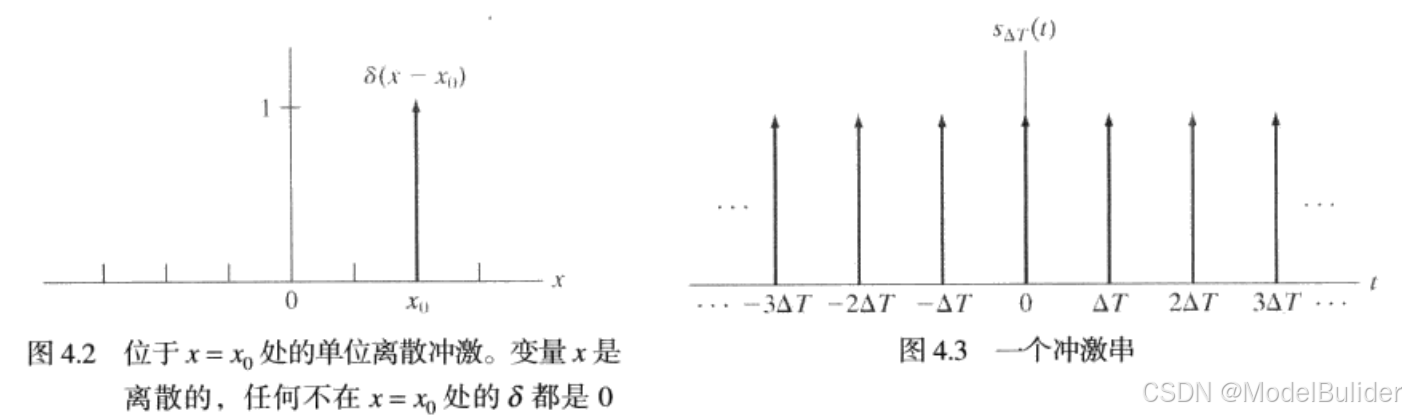
① δ ( x ) = { ∞ , x = 0 0 , x ≠ 0 \delta(x) = \begin{cases} \infty,x = 0\\ 0,x ≠ 0\\ \end{cases} δ(x)={ ∞,x=00,x=0
② ∑ x = − ∞ ∞ δ ( x ) = 1 \displaystyle\sum_{x=-\infty}^{\infty}\delta(x) = 1 x=−∞∑∞δ(x)=1
③ ∑ x = − ∞ ∞ f ( x ) δ ( x ) = f ( 0 ) \displaystyle\sum_{x=-\infty}^{\infty}f(x)\delta(x) = f(0) x=−∞∑∞f(x)δ(x)=f(0)
④ ∑ x = − ∞ ∞ f ( x ) δ ( x − x 0 ) = f ( x 0 ) \displaystyle\sum_{x=-\infty}^{\infty}f(x)\delta(x - x_0) = f(x_0) x=−∞∑∞f(x)δ(x−x0)=f(x0) - 冲激串
s △ T ( t ) = ∑ x = − ∞ ∞ δ ( t − n △ T ) s_{\triangle T}(t) = \displaystyle\sum_{x=-\infty}^{\infty}\delta(t-n\triangle T) s△T(t)=x=−∞∑∞δ(t−n△T)
2.4 连续变量函数的傅里叶变换 P128 - P130
- f(t)的傅里叶变换(FT)
F ( μ ) = ℑ { f ( t ) } = ∫ − ∞ ∞ f ( t ) e − j 2 π μ t d t F(\mu) = \Im\{f(t)\} = \int_{-\infty}^{\infty}f(t)e^{-j2\pi \mu t}dt F(μ)=ℑ{ f(t)}=∫−∞∞f(t)e−j2πμtdt - F ( μ ) F(\mu) F(μ)的傅里叶反变换(IFT)
f ( t ) = ℑ − 1 { F ( μ ) } = ∫ − ∞ ∞ F ( μ ) e j 2 π μ t d μ f(t) = \Im^{-1}\{F(\mu)\} = \int_{-\infty}^{\infty}F(\mu)e^{j2\pi \mu t}d\mu f(t)=ℑ−1{ F(μ)}=∫−∞∞F(μ)ej2πμtdμ
2.5 卷积 P130 - P131
- 卷积公式
f ( t ) ⊗ h ( t ) = ∫ − ∞ ∞ f ( τ ) h ( t − τ ) d τ f(t)\otimes h(t) = \int_{-\infty}^{\infty}f(\tau)h(t - \tau)d\tau f(t)⊗h(t)=∫−∞∞f(τ)h(t−τ)dτ - (一维)卷积定理
① f ( t ) ⊗ h ( t ) ⇐ ⇒ H ( μ ) F ( μ ) f(t)\otimes h(t) \Leftarrow\Rightarrow H(\mu)F(\mu) f(t)⊗h(t)⇐⇒H(μ)F(μ)
② f ( t ) h ( t ) ⇐ ⇒ H ( μ ) ⊗ F ( μ ) f(t)h(t) \Leftarrow\Rightarrow H(\mu)\otimes F(\mu) f(t)h(t)⇐⇒H(μ)⊗F(μ)
三、取样与取样函数的傅里叶变换 P131 - P137
3.1 取样 P131 - P132
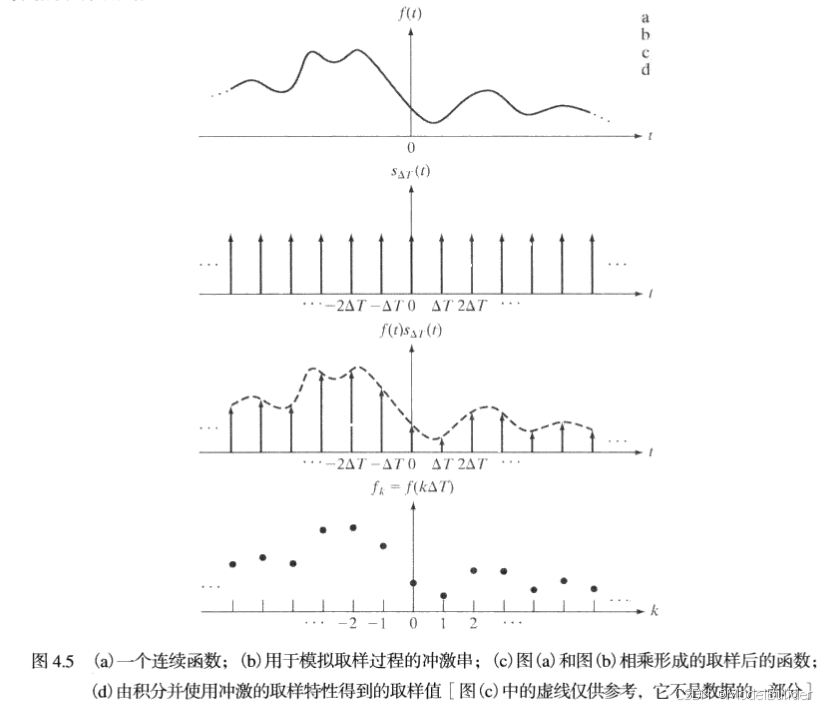
f ~ ( t ) = f ( t ) s △ T ( t ) = ∑ n = − ∞ ∞ f ( t ) δ ( t − n △ T ) \widetilde f(t) = f(t) s_{\triangle T}(t) = \displaystyle\sum_{n=-\infty}^{\infty}f(t)\delta(t - n\triangle T) f (t)=f(t)s△T(t)=n=−∞∑∞f(t)δ(t−n△T)
3.2 取样函数的傅里叶变换 P132 - P133
- F ~ ( μ ) = ℑ { f ~ ( t ) } = ℑ { f ( t ) s △ T } = F ( μ ) ⊗ S ( μ ) \widetilde F(\mu) = \Im\{\widetilde f(t)\} = \Im\{f(t)s_{\triangle T}\} = F(\mu) \otimes S(\mu) F (μ)=ℑ{ f (t)}=ℑ{ f(t)s△T}=F(μ)⊗S(μ)
- S ( μ ) = 1 △ T ∑ n = − ∞ ∞ δ ( μ − n △ T ) S(\mu) = \frac {1}{\triangle T}\displaystyle\sum_{n=-\infty}^{\infty}\delta(\mu - \frac {n}{\triangle T}) S(μ)=△T1n=−∞∑∞δ(μ−△Tn)
- F ~ ( μ ) = F ( μ ) ⊗ S ( μ ) = ∫ − ∞ ∞ F ( τ ) S ( μ − τ ) d τ \widetilde F(\mu) = F(\mu) \otimes S(\mu) = \int_{-\infty}^{\infty}F(\tau)S(\mu - \tau)d\tau F (μ)=F(μ)⊗S(μ)=∫−∞∞F(τ)S(μ−τ)dτ
= 1 △ T ∫ − ∞ ∞ F ( τ ) ∑ n = − ∞ ∞ δ ( μ − τ − n △ T ) d τ = \frac{1}{\triangle T} \int_{-\infty}^{\infty}F(\tau)\displaystyle\sum_{n=-\infty}^{\infty}\delta(\mu - \tau - \frac{n}{\triangle T})d\tau =△T1∫−∞∞F(τ)n=−∞∑∞δ(μ−τ−△Tn)dτ
= 1 △ T ∑ n = − ∞ ∞ ∫ − ∞ ∞ F ( τ ) δ ( μ − τ − n △ T ) d τ