阅读量:0
文章目录
引言
- 今天晚上七点钟到九点钟是用友集团的笔试,作为今天算法练习的主要内容!具体怎么样,晚上再说喽!
正文
小友的生产线
小友设计了一条新的生产线,在该条生产线上共有0-n种工序。每种工序之间可能存在上下游关系,如果一种工序没有下游工序,则为终点工序。如果一种工序其所有可能下游工序均可到达终点工序,则称该工序为合规工序。
给你一个有向图,其中有n个节点,表示不同种工序,以及不同工序之间的关系,请计算该条生产线中,所有的合规工序,并按照升序排列。
注意:终点工序无下游工序,默认为合规工序。
输入描述
第一行输入正整数n,表示共有n个工序节点;
接下来n行,每行有j(1<=j<n)个数,表示工序节点i与其余j个工序节点上下游关系。
注意:若工序节点i为终点工序,则j=1,且数值为-1
输出描述
- 输出一个数组,用来表示所有的合规工序,并按照升序排列
补充说明
● n == graph.length ● 1 <= n <= 104 ● 0 <= n[i].length <= n ● -1 <= n[i][j] <= n - 1 ● n[i] 按严格递增顺序排列 ● 图中可能包含自环 示例 1
- 输入
5 1 2 3 4 1 2 3 4 0 4 -1 - 输出
4 说明
- 只有工序4是终点工序,即为合规工序
示例 2
- 输入
7 1 2 2 3 5 0 5 -1 -1 - 输出
2 4 5 6 说明
工序5和6为终点工序,即为合规工序 工序2和4开始的所有下游工序最终都指向终点工序,按照升序排列最终结果为2,4,5,6
个人实现
- 这道题我是单纯使用回溯实现的,个人看来就是判定没有给节点的所有可能路径,是否可能会成环,如果会成环,那就是不可能是合理工序,如果所有可能路径都不会成环,那就是合理工序。
- 种类使用回溯实现的,具体如下
import java.util.*; // 注意类名必须为 Main, 不要有任何 package xxx 信息 public class Main { static boolean[] visited; static boolean[][] matrix; static Set<Integer> set; static List<Integer> res; static boolean dfs(int curIdx){ for(int i = 0;i < matrix[0].length;i ++){ // 判断是否存在路径 if(matrix[curIdx][i]){ // 存在成环路径,直接返回 if (visited[curIdx] || visited[i]) return false; // 存在路径,并且i是终止节点情况,直接跳过 if(set.contains(i)) continue; // 存在路径,并且i不是终点的情况,需要递归访问 visited[i] = true; if(!dfs(i)) return false; visited[i] = false; } } return true; } public static void main(String[] args) { set = new HashSet<>(); res = new ArrayList<>(); Scanner in = new Scanner(System.in); int count = in.nextInt(); visited = new boolean[count]; matrix = new boolean[count][count]; for(int i = 0;i <= count;i ++){ String line = in.nextLine(); if(i == 0) continue; if( line.isEmpty()) set.add(i); Scanner lineScn = new Scanner(line); while(lineScn.hasNextInt()){ int a = lineScn.nextInt(); if(a == -1){ set.add(i - 1); }else{ matrix[i - 1][a] = true; } } lineScn.close(); } // 遍历每一个元素 for (int i = 0;i < count ;i ++){ if(set.contains(i)) continue; //visited[i] = true; if(dfs(i)) set.add(i); Arrays.fill(visited,false); //visited[i] = false; } for(int x : set){ res.add(x); } Collections.sort(res); for(int x : res) System.out.print(x + " "); } } - 上述代码只能通过百分之四十的样例,然后剩下的怎么调节,都过不去了,这里专门复习一下,看一下一般来说怎么做的!
参考实现
- 修改如下,正常的回溯我都想了很久,正常不应该是这样的,确定了回溯的迭代条件,以及终止条件就可以直接上模板了,不应该这样的!
- 我的方法是针对无向图的环的检测,针对有向图的检测会出现问题的,这里还是建立使用三个状态来检测有向图的环,具体如下!
- 三种状态
- 0表示未访问
- 1表示正在访问
- 2表示已经访问,处理过当前节点,当前节点后续是不存在环的,直接跳过就行了!
boolean isCyclicUtil(int v,int[] visited){ // 当前路径下确实存在环 if(visited[v] == 1) return true; // 检测是否已经是访问过的点 if(visited[v] == 2) return false; visited[v] = 1; for(int neighbour:adj.get(v)){ if(isCyclicUtli(neighbour,vivited)){ return true; } } visited[v] = 2; return false; } public boolean isCyclic() { int[] visited = new int[V]; for (int i = 0; i < V; i++) { if (isCyclicUtil(i, visited)) { return true; } } return false; } 三个状态,11成环,22非环,12中间是循环
小友策划游戏人物
- 小友是一个游戏策划,他计划设计一个新人物,该人物的攻击模式较为特殊:他的附加攻击力可以拆分为n份(n>=2),这n份的乘积作为最终伤害值。游戏总监认为该人物过于超模(过于强大),要求对其附加攻击力增加上限限制。
- 现在给你最终伤害值的上限和该人物的附加攻击力,请判断该人物的实际最终伤害值是否会超出给出的最终伤害值上限。
- 输入描述
输入两个数值,第一个数值为最终伤害值上限,第二个数值为该人物的附加攻击力。 例如:2920 22 2920为最终伤害值的上限 22为该人物的附加攻击力 - 输出描述
输入true或者false true表示超出上限 false表示未超出上限 - 补充说明
最终伤害值上限不会超过int最大值 示例一
- 输入
1 2 - 输出
false - 说明
最终伤害上限1 附加攻击力2 2=1+1 1*1=1 所以未超过上限 个人实现
- 我用的方法应该是有问题的,是拆成尽可能大的两个数字的乘积,然后在计算最大值,具体如下
import java.util.Scanner; public class Main { public static void main(String[] args) { Scanner in = new Scanner(System.in); int maxV = in.nextInt(); int att = in.nextInt(); long maxAtt = 0; for(int i = 2;i <= att;i ++){ long tempAtt = (long) (Math.pow(i, (double) att / i) * (att % i)); maxAtt = Math.max(maxAtt,tempAtt); } System.out.println(maxAtt > maxV); } } - 这个题目还是要想想使用动态规划怎么做
参考实现
- 之前学了那么久的闫氏DP分析法,这里得想想看怎么弄分析,从集合的角度出发!这道题目对于任意的数字都可以分成两个数字,然后划分点是从第一个点往后遍历到最终的结果,具体如下图
import java.util.Scanner; public class Main { public static void main(String[] args) { Scanner in = new Scanner(System.in); int maxV = in.nextInt(); int att = in.nextInt(); int[] dp = new int[att + 1]; dp[0] = 0; dp[1] = 0; dp[2] = 1; for(int i = 2;i <= att;i ++){ for(int j = 1;j < i;j ++){ dp[i] = Math.max(dp[i], Math.max(j * (i - j), Math.max(dp[j] * dp[i - j], Math.max(j * dp[i - j],dp[j] * (i - j))))); } } System.out.println(dp[att]); } } 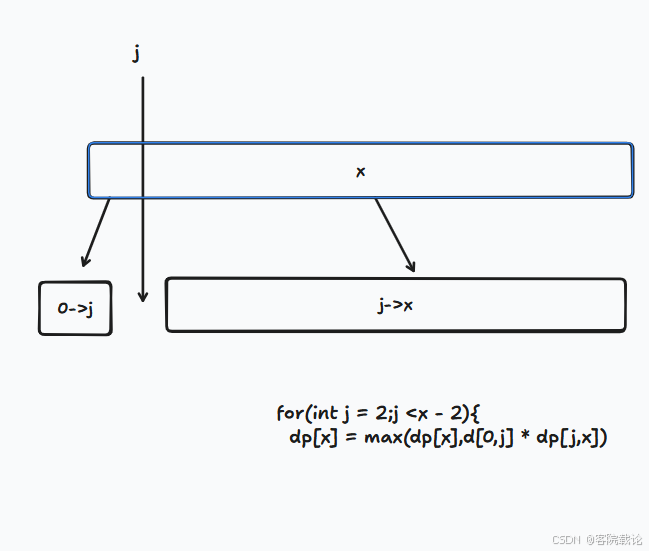
最佳工作任务安排
- 小友所在的部门在进行一系列复杂的开发项目。为了优化开发流程,部门要求工程师在不同的任务之间切换。每个任务有不同的执行时间,有些任务因为各种原因无法进行(标记为-1)。工程师可以在规定的跳跃范围内从一个任务跳到另一个任务,但每次执行任务需要消耗相应的时间。
- 你的目标是找到一个从任务列表开头到结尾的执行顺序,使得总执行时间最小。如果存在多个总执行时间相同的顺序,返回按索引值更小优先的顺序。如果无法到达最后一个任务,返回一个空数组。
规则
1.输入一个整数数组 tasks 表示任务执行时间,长度为 n。 2.输入一个整数 maxStep 表示单次切换任务的最大切换长度。 3.你从任务列表的第一个任务开始(tasks[0] 不是 -1)。 4.从任务 i 切换到任务 j,消耗的时间为 tasks[j]。 5.如果你当前位于任务 i,你只能跳到任务 i + k(满足 i + k <= n),其中 k 在范围 [1, maxStep] 内。 6.返回一个整数数组,包含你访问的任务索引顺序,使得总执行时间最小。如果存在多个总执行时间相同的顺序,返回索引值更小的顺序。 排序说明
如果存在多个总执行时间相同的顺序: 假设方案 p1 = [Pa1, Pa2, ..., Pax] 和方案 p2 = [Pb1, Pb2, ..., Pbx]。 如果在两个方案中第一个不同的索引 j 处,Pa[j] 小于 Pb[j],则选择方案 p1。 如果所有索引都相同,但任务切换次数不同,则选择任务切换次数较少的一个方案。 提示:注意排序规则,如 1-2-3-4-5 和 1-4-5 , 假设两个方案所消耗的时间成本相同, 那么前面的方案更优。 输入描述
整数 N,代表任务 tasks 的长度 长度为 N 的数组 tasks 的各个元素 整数 M,代表每次切换任务的最大跳跃长度 输出描述
输出数组,代表总执行时间最短,并且索引值最小的执行方案 补充说明
1 <= tasks.length <= 1000 -1 <= tasks[i] <= 100 tasks[0] != -1 1 <= maxStep <= 100 示例 1
输入
5 1 2 4 -1 2 2 输出
1 3 5 个人实现
- 我单纯使用回溯实现的,因为我知道如果使用用DP只能求出来对应最大值,但是没有办法求出来具体路径,如果要求出来具体的路径,还是得使用回溯,所以,为了节省时间,直接写了两边回溯!
- 中间本来想改成优先队列的,后来没时间改,就冲写了一个,原来的优先队列有没闪,下面是考试中的原来的代码,还没来及的复制上去!
import java.sql.Array; import java.util.ArrayList; import java.util.List; import java.util.PriorityQueue; import java.util.Scanner; public class Main { static int[] task; static PriorityQueue<List<Integer>> pq; static List<Integer> list; static List<Integer> res; static int maxV = 0; static int skipLen ; static void dfs(int curIdx ){ if(curIdx < task.length && task[curIdx] == -1) return ; if(curIdx == task.length){ int sum = 0; for(int i =0;i < list.size() - 1;i ++) sum += task[i]; maxV = Math.max(maxV,sum); } // 遍历当前路径下的所有的步骤 for (int i = 1; i <= skipLen && (curIdx + i) <= task.length;i ++ ){ list.add(curIdx + i); dfs(curIdx + i); list.remove(list.size() - 1); } } static void dfs2(int curIdx ){ if(curIdx < task.length && task[curIdx] == -1) return ; if(curIdx == task.length){ int sum = 0; for(int i =0;i < list.size() - 1;i ++) sum += task[i]; //System.out.println(sum); if(sum == maxV){ if(res == null) res = list; else if(res.size() > list.size()) res = new ArrayList<>(list); } } // 遍历当前路径下的所有的步骤 for (int i = 1; i <= skipLen && (curIdx + i) <= task.length;i ++ ){ list.add(curIdx + i); dfs2(curIdx + i); list.remove(list.size() - 1); } } public static void main(String[] args) { Scanner in = new Scanner(System.in); int count = in.nextInt(); task = new int[count]; for(int i = 0;i < count;i ++) task[i] = in.nextInt(); skipLen = in.nextInt(); pq = new PriorityQueue<>((List<Integer> a,List<Integer> b)->{ int sumA = 0; for(int x:a) sumA += x; int sumB = 0; for(int x:b) sumB += x; return Integer.compare(sumA,sumB); }); list = new ArrayList<>(); dfs(0); dfs2(0); if(res == null) System.out.println("[]"); else{ System.out.println("1 "); for(int i = 0;i < res.size();i ++) System.out.print(res.get(i) + 1 + " "); } // if(!pq.isEmpty()) // for(int i = 0;i < pq.peek().size();i ++) // System.out.print(pq.peek().get(i) + " "); // else // System.out.println("[]"); } } 参考实现
还是最后一个状态为目标进行分析,假设可以跳跃K步,然后最后一步有几种可能
f[k] = x[k] + f[k - i] ,i从零到k - 然后选取上述值的最大值,如果f[k]是-1,中间就是断层的。
import java.util.*; public class Main { public static void main(String[] args) { Scanner scanner = new Scanner(System.in); // 读取输入 int N = scanner.nextInt(); int[] task = new int[N]; for (int i = 0; i < N; i++) { task[i] = scanner.nextInt(); } int M = scanner.nextInt(); // 初始化 dp 数组 final int INF = Integer.MAX_VALUE; // 使用 Integer.MAX_VALUE 代替 inf int[] f = new int[N]; Arrays.fill(f, INF); f[0] = 0; int[] fm = new int[N]; Arrays.fill(fm, -1); // 动态规划 for (int i = 1; i < N; i++) { if (task[i] == -1) continue; for (int k = 1; k <= M; k++) { if (i - k < 0) break; if (f[i - k] + task[i] < f[i] && task[i - k] != -1) { f[i] = f[i - k] + task[i]; fm[i] = i - k; } } } // 回溯找到路径 List<Integer> res = new ArrayList<>(); int index = N - 1; while (true) { if (index == 0) { res.add(1); break; } res.add(index + 1); index = fm[index]; } // 输出结果 Collections.reverse(res); // 反转列表以从起点到终点 for (int r : res) { System.out.print(r + " "); } scanner.close(); } } 大众评分最高的一次旅程

总结
- 很难受,今天的题目偏难,不过能够写出来三道题,然后第三道题写完了,没来得及复制上去,好可惜!
- 不过今天也反应出来很多问题,就是我的笔试能力还是不够!代码写的太慢了,尤其是回溯!
- 最后一题,我连题目都没有见到,就不放在这里了!跳过了!

