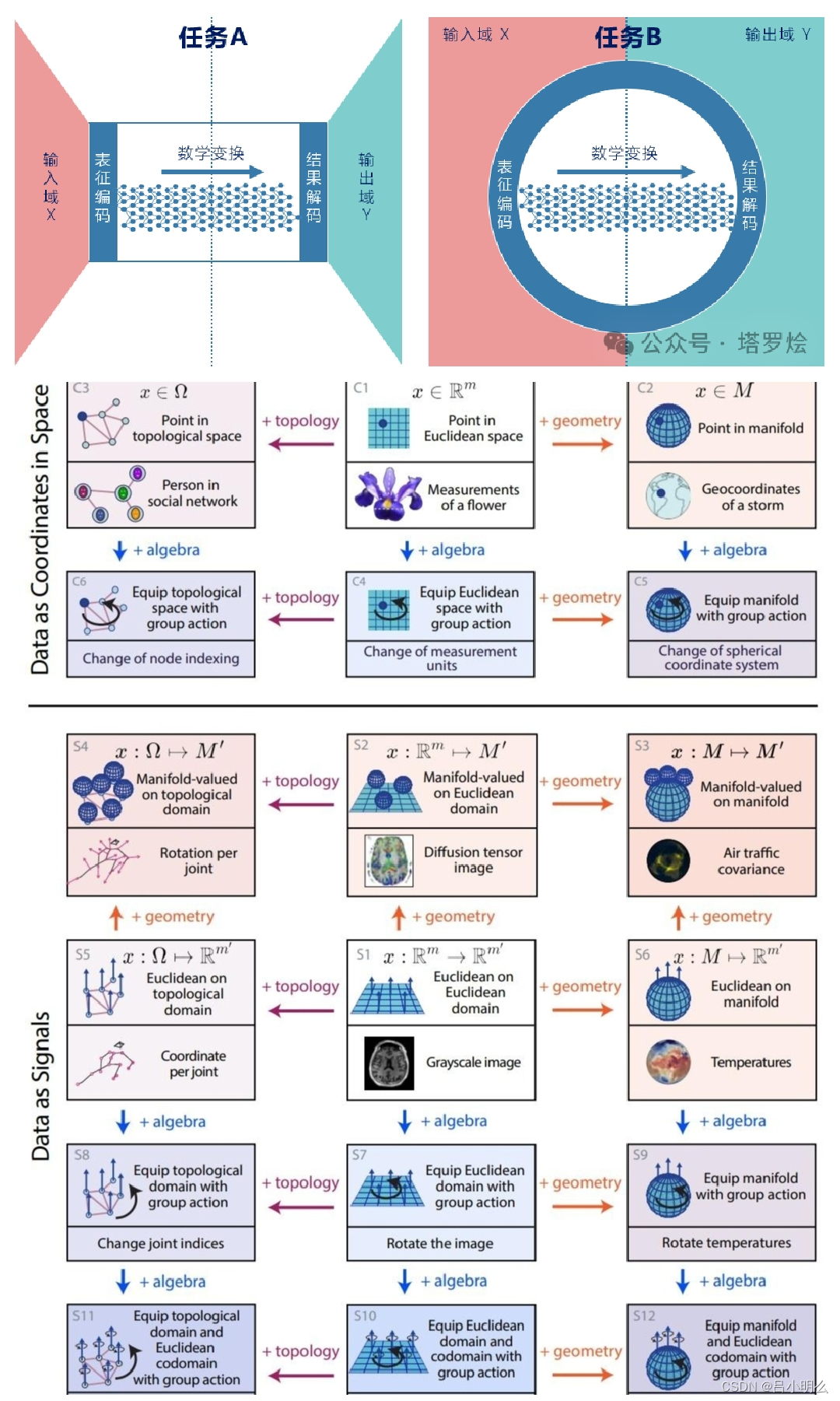
探究in context或Prompt对于LLM来说其根本意义,in context & Prompt Learning带给我们更深一层的提示是什么?
文章里的探索希望能够将in context或Prompt置身于一个更全局的视角来看待:将其视为在真实世界中时空认知流形所映射为数据流形表征分布中的前置部分,即可以将其看待为任何物理与概念时空下的前置流形分布条件,需要关注于这种“前置”作为整体数据流形或认知流形的组成与影响,其控制或引导着全局流形的分布与轨迹。
另外一方面,从模型推理的全局视角来看,对于Xn+M→Yn来说,Xn∪Yn可作为整体广义层面的认知数据流形分布来看待,其中M作为中间模型节点,用于对齐并衔接Xn与Yn的广义流形分布(在现实中人们在认知行为中总是自然的通过Xn+M对Yn进行着推理到决策)。在以往的探索中我们之前将目光更多聚焦在M之后的Yn,并探索Yn在生成的内容上所体现出不论在system1与system2间不同流形分布在复杂推理模式上的差异和本质上的等价(当然探索初衷是希望能够合理、平滑的构建出其中的M,并延展到探寻system1与system2间数据/信号变换模式上的本质),而反观对于Xn确很少讨论。
然而随着逐步的探索,发现其Xn本身应与Yn有着同等的研究探索价值,如在当下热度比较高的长文本处理,对应延展出的transformer/manba/TTT不同模型结构对Xn的表征与压缩的平衡。
而我想未来的探索也不仅仅局限于文本的长度上,而应更深入的全局探索M对Xn→Yn所蕴含的复杂信息结构对齐及表征分布。包括考虑Xn与Yn之间相互作用于不同时空或不同模态间鬼魅般的纠缠(如Prompt思想,以stepbystep为代表的泛xot的延伸),两者与M间一定存在着更深邃而复杂的内涵联系 - 如现在表面上看起来M中的transformer/manba/ttt等实现对Xn的刻画与表征,并通过mlp或kan等模拟逼近了Xn→Yn世界的分布。而我相信随着继续对其进行深入的研究与探索,在未来将不光局限于模型算法(M)本身在网络结构或数学方法的革新,还将包括针对不同模态、时空结构、推理决策空间表征下更深刻的思想运用,如从llm的AR到cv的diffusion思想延展,找到平衡探索与利用的MCTS或所谓的Q*s方法...以及M在Xn∪Yn的→下的动态动态对齐衔接。