DP动态规划入门（数字三角形、破损的楼梯、安全序列）_业界新闻

发布时间:2024-08-03 10:52

阅读量:0

一、动态规划（DP）简介

动态规划（Dynamic Programming，简称DP）是运筹学的一个分支，它是一种通过将复杂问题分解成多个重叠的子问题，并通过子问题的解来构建整个问题的解的算法。在动态规划中，有几个核心概念需要理解：

状态：状态通常表示为形如dp[i][j] = val的取值，其中i和j是用于描述和确定状态所需的变量（下标），而val则是该状态对应的值。
状态转移：状态转移描述了不同状态之间如何相互转化。这通常可以表示为一个数学表达式，而转移的方向则决定了算法是迭代还是递归地进行。
最终状态：最终状态即题目所要求解的状态，也是我们通过动态规划算法最终要得到的答案。

动态规划的关键在于找到子问题之间的重叠关系，并存储这些子问题的解以避免重复计算。通过这种方式，动态规划能够在多项式时间内解决一些看似复杂的问题，如背包问题、最短路径问题等。在实际应用中，动态规划被广泛用于优化和控制问题，以及计算机视觉、生物信息学等领域。

二、动态规划的解题步骤

步骤一：确定状态

首先，需要明确问题的状态表示。在动态规划问题中，状态通常定义为“到第i个为止，xx为j（xx为k）的方案数/最小代价/最大价值”等。这里，“i”、“j”和可能的“k”是状态的参数，它们根据具体问题而定。状态的确切定义取决于问题的性质和所需优化的目标（如最小代价、最大价值或方案数）。

步骤二：确定状态转移方程

状态转移方程是动态规划的核心，确定状态转移方程，即从已知状态得到新状态的方法，并确保按照这个方向一定可以正确地得到最终状态。根据状态转移的方向来决定使用迭代法还是递归法（记忆化）。状态转移方程的确立通常基于问题的特定条件和约束。

步骤三：确定最终状态并输出

最终状态通常是问题的解所对应的状态。在确定了状态转移方程后，我们需要按照这个方程迭代或递归地计算出所有可能的状态，直到达到最终状态。最终状态可能是通过迭代法逐步累积得到，也可能是通过递归法（结合记忆化以避免重复计算）逐步回溯得到。一旦到达最终状态，我们就可以根据问题的要求输出相应的解，如最小代价、最大价值或特定条件下的方案数。

综上所述，这三个步骤——确定状态、确定状态转移方程和确定最终状态并输出——构成了动态规划求解问题的一般框架。在实际应用中，根据具体问题的不同，这些步骤的具体实现方式也会有所不同。

三、线性DP例题

（一）数字三角形（最大路径）

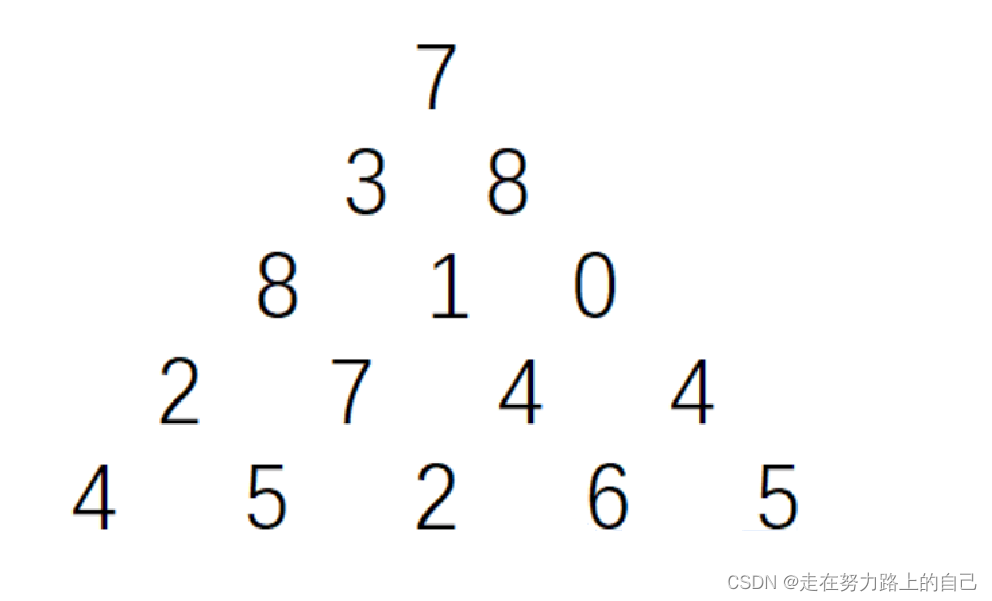
上图给出了一个数字三角形。从三角形的顶部到底部有很多条不同的路径对于每条路径，把路径上面的数加起来可以得到一个和，你的任务就是找到最大的和(路径上的每一步只可沿左斜线向下或右斜线向下走)。
输入描述
输入的第一行包含一个整数 N(1 ≤ N < 100)，表示三角形的行数。
下面的 N 行给出数字三角形。数字三角形上的数都是 0 至 99 之间的整数。
输出描述
输出一个整数，表示答案。
输入样例

5 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5

输出样例

30

思路：

从最后一层向上，取最大值累加。
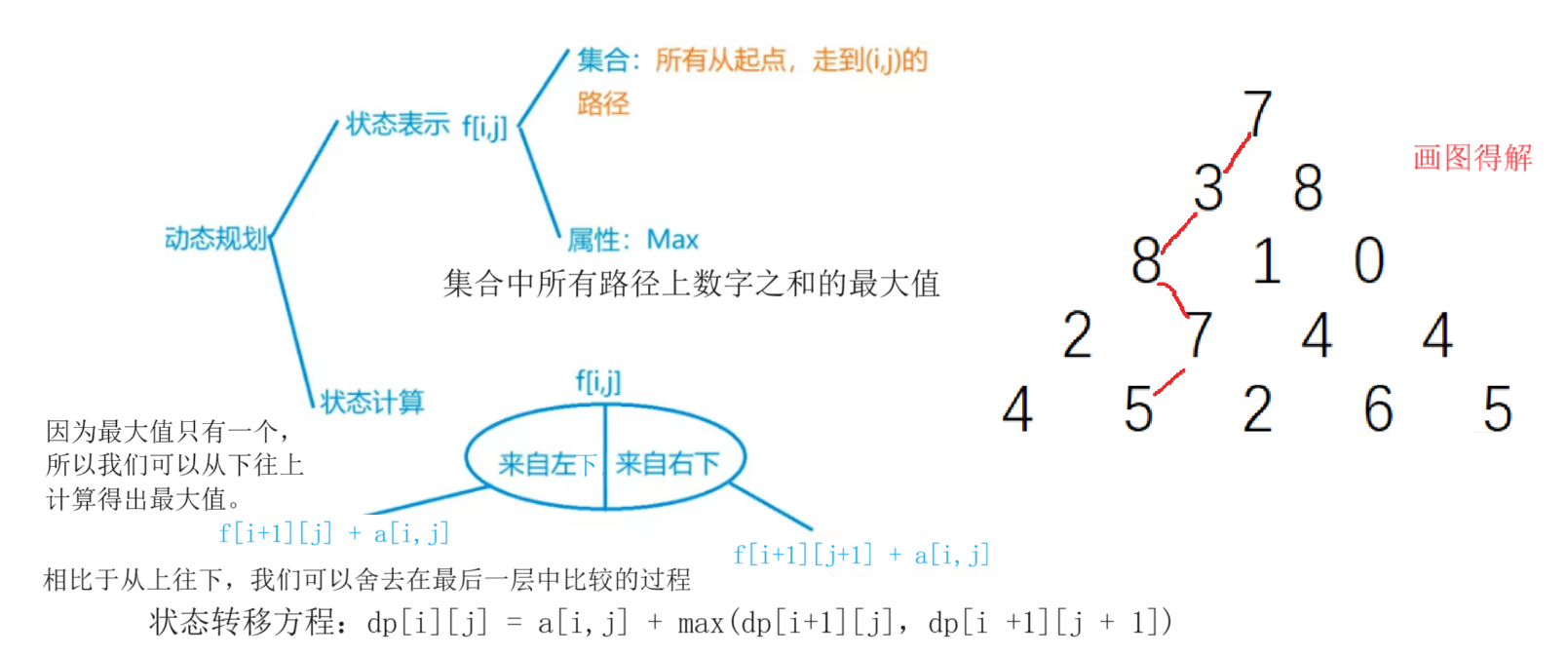
确定状态：设状态dp[ i ][ j ] = a[ i ][ j ] + max(dp[ i + 1 ][ j ], dp[ i + 1 ][ j + 1 ])；
状态转移方程为dp[i][j]=max(dp[i+1][j]，dp[i +1][j + 1]) ；
因为这里需要用下面的状态更新上面的，所以我们应该从下往上进行状态转移。最后输出dp[1][1]

解法一：自下而上

#include<bits/stdc++.h> using namespace std; using ll = long long; const int N = 105; ll a[N][N], dp[N][N];  int main() { 	int n; cin >> n; 	for (int i = 1; i <= n; ++i) 		for (int j = 1; j <= i; j++) 			cin >> a[i][j]; 	for (int i = n; i >= 1; i--) 		for (int j = 1; j <= i; j++) 			dp[i][j] = a[i][j] + max(dp[i + 1][j], dp[i + 1][j + 1]); 	cout << dp[1][1] << '\n'; 	return 0; }

解法二：自上而下

#include<bits/stdc++.h>   using namespace std; const int N = 105; int a[N][N], f[N][N]; int n, INF = 1e9;  int main() { 	cin >> n; 	for (int i = 1; i <= n; i++) 		for (int j = 1; j <= i; j++)cin >> a[i][j]; 	for (int i = 0; i <= n; i++) 		for (int j = 0; j <= i; j++)f[i][j] = -INF; 	f[1][1] = a[1][1];  	for (int i = 2; i <= n; ++i) 		for (int j = 1; j <= i; ++j) 			f[i][j] = max(f[i - 1][j - 1], f[i - 1][j]) + a[i][j]; 	int res = -INF; 	for (int i = 1; i <= n; i++)res = max(res, f[n][i]);  	cout << res; 	return 0; }

（二）破损的楼梯（方案数）

问题描述：
小蓝来到了一座楼梯前，楼梯共有N级台阶。从第0级台阶出发，小蓝每次可以迈上1级或2级台阶。但是，楼梯上的第a1级、第a2级、第a3级，以此类推，共M级台阶的台阶面已经坏了，不能踩。

小蓝想要到达楼梯的顶端，即第N级台阶，且不能踩到坏台阶。请问他有多少种到达顶端的方案数？由于方案数可能很大，请输出结果对取模的值。

样例输入

6 1 3

样例输出

4

思路：

确定状态：状态dp[ i ]表示走到第 i 级台阶的方案数。
确定状态转移方程：在正常的楼梯上，我们可以从第i - 1级台阶或第i - 2级台阶走到第 i 级台阶，因此状态转移方程为dp[ i ] = dp[ i－1 ]+dp[ i - 2 ]。
然而，如果第 i 级台阶是破损的，则不能走到该台阶，此时我们需要将dp[ i ]设为0。
最后我们输出dp[ n ]，表示走到第 n 级台阶的方案数

#include<bits/stdc++.h> using namespace std; const int p = 1e9 + 7; int n, m; int main() { 	cin >> n >> m; 	vector<int>dp(n + 1, 1);int temp = 0; 	for (int i = 1; i <= m; i++) 	{ 		cin >> temp; 		dp[temp] = 0; 	} 	for (int i = 2; i <= n; i++) 	{ 		if (!dp[i])continue; 		dp[i] = (dp[i - 1] + dp[i - 2]) % p; 	} 	cout << dp[n] << '\n'; 	 	return 0; }

（三）安全序列（方案数）

问题描述
小蓝是工厂里的安全工程师，他负责在工厂里安全地放置危险品油桶。工厂的空位排列成一条直线，共有n个空位。小蓝需要按照特定的规则在这些空位上放置油桶：每两个油桶之间至少需要k个空位隔开。现在，小蓝想知道有多少种不同的放置方案可以满足这些条件。由于可能的方案数非常大，输出结果需要对10^9 + 7取模。
输入格式
输入包含两个正整数n和k，分别表示空位的数量和每两个油桶之间至少需要的空位数。
输出格式
输出一个整数，表示满足条件的放置方案数对10^9 + 7取模的结果。
样例输入
4 1
样例输出
6
说明
在样例中，有4个空位，每两个油桶之间至少需要1个空位。可能的放置方案有6种，分别是：0000（不放任何油桶），1000，0100，0010，0001和1001（其中1表示放置油桶，0表示不放）。注意，这里的方案数已经对10^9 + 7取模。
评测数据规模
对于所有评测数据，1 ≤ n ≤ 10^9，1 ≤ k ≤ n-1。

思路：

首先，我们定义dp[i]为在前i个空位中放置油桶的方案数。然后，我们需要计算前缀和数组prefix。对于每个位置i，prefix[i]表示从位置0到位置i为止的所有放置方案数的总和。

ll dp[N], prefix[N];

循环遍历判断每个位置之前没有足够的空间放置另一个油桶。

如果当前位置减去k再减1小于1，则dp[ i ]为1。

否则，dp[ i ]的值等于前缀和数组在( i - 1 - k )位置的值。

if (i - k - 1 < 1)dp[i] = 1; else dp[i] = prefix[i - 1 - k];

设状态dp[ i ]表示以位置i结尾的方案总数，状态转移方程： $dp[i] = \sum_{j=1}^{i-k-1}dp[j]$

但是直接去求和肯定会超时，所以我们需要利用前缀和来优化时间复杂度（注意取模）。

prefix[i] = (prefix[i - 1] + dp[i]) % p;

计算到当前位置为止，包括所有符合条件的放置方案数的总和。

#include<bits/stdc++.h> using namespace std; using ll = long long; const ll N = 1e6 + 9, p = 1e9 + 7;  ll dp[N], prefix[N];  int main() { 	int n, k; cin >> n >> k; 	dp[0] = prefix[0] = 1;// 初始化dp和prefix数组的第0项为1，表示空序列的方案数为1 	for (int i = 1; i <= n; ++i)// 遍历1到n，计算每个位置的dp值和前缀和 	{ 		if (i - k - 1 < 1)dp[i] = 1; 		// 如果当前位置减去k再减1小于1，则dp[i]为1 		// 说明在当前位置之前没有足够的空间放置另一个油桶， 		// 因此在这种情况下，只能选择不放置油桶，所以'dp[i]'被设为'1'。 		else dp[i] = prefix[i - 1 - k]; 		// 否则，dp[i]的值等于前缀和数组在(i-1-k)位置的值 		// 这表示从位置'0'到位置'i-k-1'的所有放置方案数。 		// 这样做是因为每两个油桶之间需要至少'k'个空位， 		// 因此'dp[i]'实际上继承了在'i-k-1'位置及之前能放置油桶的所有方案。  		prefix[i] = (prefix[i - 1] + dp[i]) % p; 		// 计算到当前位置为止，包括所有符合条件的放置方案数的总和，并将结果模上'p'以防溢出。 	} 	cout << prefix[n] << '\n';  	return 0; }

今天就先到这了！！！