阅读量:0
1.原始文档
《用于正弦波频率估计的修正I-Rife算法》,王哲文,2024
DOI: 10. 16337/j. 1004‑9037. 2024. 02. 019
1.1 这篇论文所属的自科基金U21A20500:近5年所承担的重要科研项目表-智能感知系统与安全教育部重点实验室(湖北大学)

2.问题速记
2.1 摘要部分
- 量化频点的因素
- 为啥接近量化频谱点处会有更大的误差?他不应该更小吗?
- 文章的中心是Rif算法的性能和误差分析以及针对性改进
- 0.5 pt???how?
- 论文复杂度与I-Rif相当
- I-Rif算法
- 移频因子
- Rif算法区别
- 修正的基本逻辑
- 克拉美-罗下界
- 均方根误差
- Cramer-Rao lower Bound
- 关键词:
- 频率估计Freq estimation
- 细化谱 spectrum subdivision
- CRLB
- 中国分类TN957.51
- 文献标志码:A
- Sinusoid Wave
2.2 引言部分
- 调频连续波Frequency modulation continuous waveFMCW)雷达
- 混频
- 中频信号
- 距离速度
3.频率估计的途径
- Abatzoglou 最大似然估计最大似然估计(Maximum likelihood ML)算法
- FFT 频谱泄露、栅栏效应
- 信噪比较低时误差很大
- 基于FFT的插值算法
- 三谱线插值法
- 迭代差值法
- 抛物线内插
- 双线性对称频率内插
- Rif算法★
- 异频相位处理
- 全相位时移相位差频率估计
- 能量重心矫正法
- 相位差分算法
- 频谱细化方法的Zoom‑FFT算法★
- 线性调频变换CZT算法★
ML慢而精确。RIf快,Zoom-FFT, CZT性能很好但无法满足实时解析场景。
3.1 Rif算法
- Rife1970年提出,利用幅度最高谱线与相邻谱线,差值,确定真实频率。
- 当信噪比过低或其真实频率接近量化频率时,易出现插值方向的错误从而引起较大的
误差。 - Quinn提出用最大谱线,次大谱线的之比的实部来替代幅值之比
- 邓帧淼M-Rif,引入移频原理,将估计的频率移到两个量化频率中心,再差值,移频量固定1/3
- 有时需要二次移频
- 王宏位I-Rif,频谱细化,移频
- 孙宏君P-Rif,相角
- A-P-Rif幅值相角判据的改进频移门限值来确定是否使用相角判据,得到了精度更高的估计性能
- 叶茂Z-Rif
- 在A-P-Rif上,幅值相角规律
- NianA-Rif
- 基于估计
3.2 Rif算法的实际性能与误差
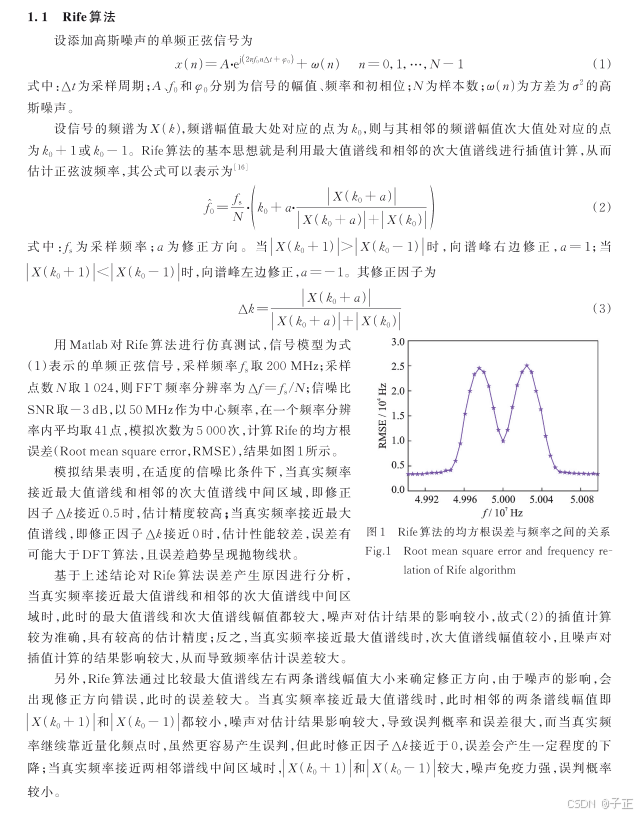
4.Python重现Rif算法和上述现象
4.1 准备信号源
我的基本信号处理对象是振动信号,这里生成了一个冲击性振动信号,很简单: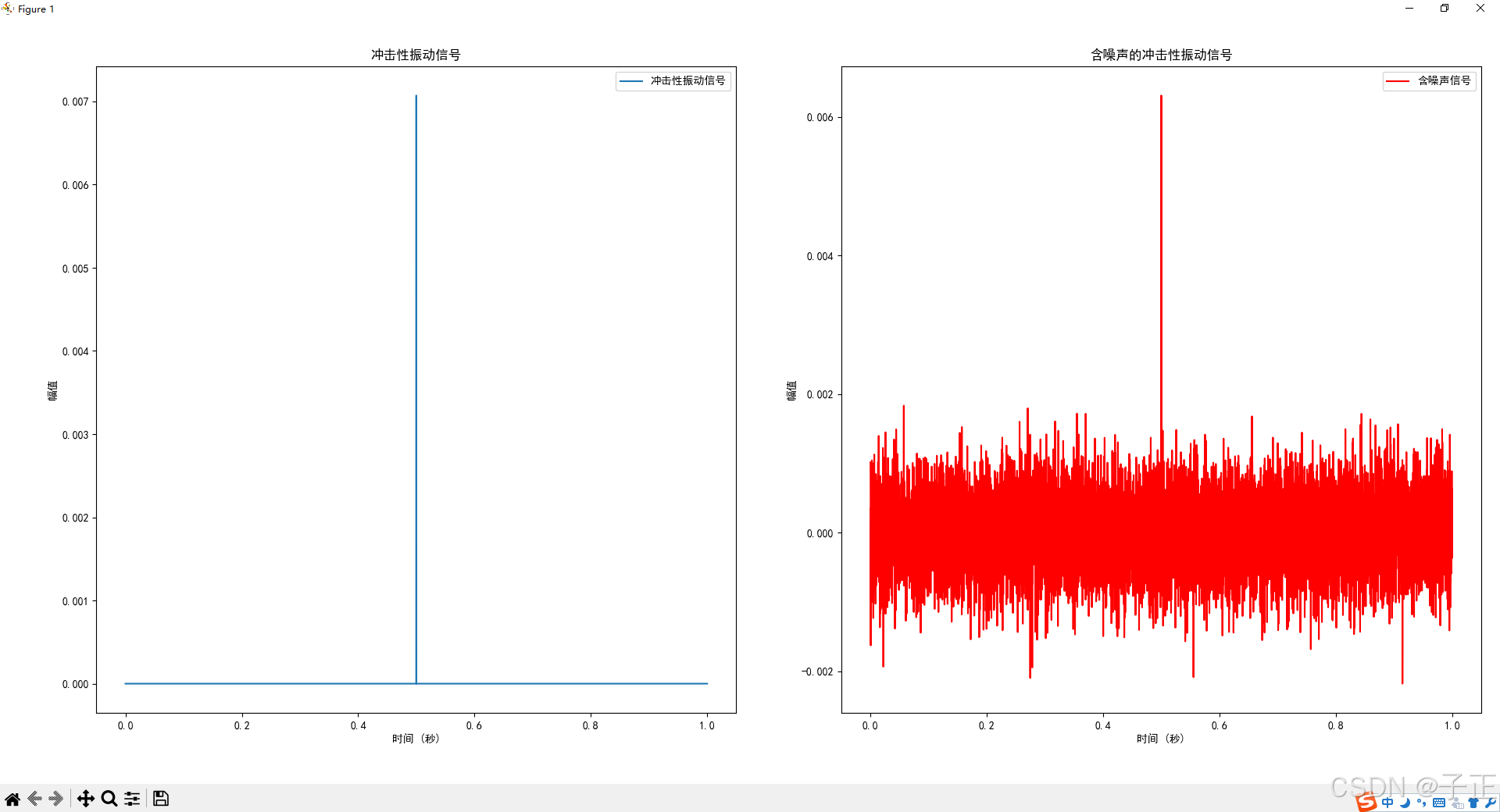
叠加了幅度为信号-20db的高斯噪声。生成代码参见附录B 冲击信号模拟源
4.2 使用不同的采样率去采集信号源,生成多组采样数据
附录A 一些可用的三方库
1. specutils
这是一个用于天文观测雷达信号的解析库,作为一个完整领域的信号分析库,可以用来对信号处理的可能问题和算法有一个大致的第一印象。
download from: specutils · PyPId
doc:Specutils Documentation — specutils v1.15.1.dev0+gce3f43c.d20240501
附录B 源码
1. 冲击信号模拟源
#!/usr/bin/env python3 # -*- coding: utf-8 -*- # 获取当前脚本文件所在目录的父目录,并构建相对路径 import os import sys current_dir = os.path.dirname(os.path.abspath(__file__)) project_path = os.path.join(current_dir, '..') sys.path.append(project_path) sys.path.append(current_dir) import numpy as np import matplotlib.pyplot as plt from matplotlib import rcParams from scipy.signal import get_window # 设置中文字体 rcParams['font.sans-serif'] = ['SimHei'] # 指定中文字体 rcParams['axes.unicode_minus'] = False # 解决负号问题 # 参数设置 fs = 10000 # 采样频率 (Hz) f_signal = 181.5 # 信号频率 (Hz) rms_signal = 5e-3 # 信号 RMS (m/s) duration = 1 # 信号持续时间 (秒) pulse_duration = 1 / (100 * f_signal) # 脉冲持续时间 (秒) # 生成时间序列 t = np.arange(0, duration, 1/fs) # 生成冲击性振动信号(脉冲信号) pulse_start = int(fs * (duration / 2 - pulse_duration / 2)) pulse_end = int(fs * (duration / 2 + pulse_duration / 2)) signal = np.zeros_like(t) signal[pulse_start:pulse_end] = rms_signal * np.sqrt(2) # 生成高斯噪声 rms_noise = rms_signal * 0.1 noise = rms_noise * np.random.randn(len(t)) # 将信号和噪声相加 signal_with_noise = signal + noise # 绘图 plt.figure(figsize=(12, 6)) plt.subplot(1, 2, 1) plt.plot(t, signal, label='冲击性振动信号') plt.title('冲击性振动信号') plt.xlabel('时间 (秒)') plt.ylabel('幅值') plt.legend() plt.subplot(1, 2, 2) plt.plot(t, signal_with_noise, label='含噪声信号', color='red') plt.title('含噪声的冲击性振动信号') plt.xlabel('时间 (秒)') plt.ylabel('幅值') plt.legend() plt.tight_layout() plt.show()