前言
AStar(A*)算法,是一种在静态网格中求解最短路径直接有效的搜索方法。在游戏开发中,A*算法常应用于部分RPG游戏和策略战棋类游戏。对于Unity开发者来说,掌握A*算法也是十分有必要的。不过在了解A*算法之前,有必要先回顾一下深度优先算法(DFS)、广度优先算法(BFS)以及迪杰斯特拉算法(Dijkstra),这是理解和掌握A*算法的必要基础。
深度优先算法(DFS)
所谓深度优先,通俗一点解释就是:先选择一个方向头也不回的一条路走到黑,再回头从另一个方向又一条路走到黑,如此往复直到走遍整张图。
算法的基本流程是:
- 获取给定起点周围未访问的邻接节点
- 对这些邻接节点进行递归,直到所有节点访问完毕
private void StartDFS(int x, int y, bool[] visits = null) { if (visits == null) { visits = new bool[map.Length * map[0].Length]; } if (x >= 0 && x <= map.Length && y >= 0 && y <= map[0].Length) { int index = x + y * map.Length + 1; if (!visits[index - 1]) { visits[index - 1] = true; Debug.Log("(x:+" + x + ",y:" + y + ")"); StartDFS(x - 1, y, visits);//左边的邻接节点 StartDFS(x + 1, y, visits);//右边的邻接节点 StartDFS(x, y - 1, visits);//下边的邻接节点 StartDFS(x, y + 1, visits);//上边的邻接节点 } } } 
上面我的访问优先级是左、右、下、上。
为了更好地进行理解,可以调换一下顺序,比如:上、右、下、左
StartDFS(x, y + 1, visits);//上 StartDFS(x + 1, y, visits);//右 StartDFS(x, y - 1, visits);//下 StartDFS(x - 1, y, visits);//左广度优先算法(BFS)
而广度优先顾名思义就是优先访问周围的邻接节点,像水流一样慢慢的向外扩张,直到走遍整张图。
算法的基本流程是:
- 把给定起点入队
- 从队列中出队一个点
- 获取该点周围邻接的未访问节点,并逐个入队
- 重复2,3步骤直到所有点访问完毕
private void StartBFS(int x, int y) { bool[] visits = new bool[map.Length * map[0].Length]; Queue<int> bfs = new Queue<int>(); int index = x + y * map.Length + 1; bfs.Enqueue(index); visits[index - 1] = true; while (bfs.Count > 0) { int currIndex = bfs.Dequeue(); int currX = (currIndex - 1) % map.Length; int currY = (currIndex - 1) / map.Length; m_QueuePoints.Enqueue(currIndex); AddPoint(currX - 1, currY, bfs, visits); AddPoint(currX + 1, currY, bfs, visits); AddPoint(currX, currY - 1, bfs, visits); AddPoint(currX, currY + 1, bfs, visits); } } private void AddPoint(int x, int y, Queue<int> bfs, bool[] visits) { if (x >= 0 && x <= map.Length && y >= 0 && y <= map[0].Length) { int index = x + y * map.Length + 1; if (!visits[index - 1]) { bfs.Enqueue(index); visits[index - 1] = true; } } }
迪杰斯特拉算法(Dijkstra)
然而不管是深度优先(DFS)还是广度优先(BFS)都只是在逐个遍历一张图,当图中有两点A和B并且要计算出从A点到B点的最短路线时应该如何去规划?于是Dijkstra提出了一种最短路径算法。
简单来说,Dijkstra算法就是在广度优先(BFS)的基础上,优先选择移动消耗最低的节点,并在广度优先(BFS)的遍历过程中逐步累加该点周围邻接节点的移动消耗,直到找到目标点为止。
算法的基本流程是:
- 把给定起点入队,设置该点移动消耗为0
- 出队一个点,获取该点周围可以移动的邻接节点,然后检测这些邻接节点是否被访问过
- 若已经被访问过,检测当前点移动到该邻接节点的移动消耗,是否比该邻接节点的移动消耗更低,并对该邻接节点的移动消耗进行更新
- 若没有访问过,则累加该邻接节点的移动消耗
- 从所有节点中选择一个移动消耗最低并没有被访问过的点并把该点入队
- 重复2,3,4,5直到找到目标点。
private void StartDijkstra(int x, int y) { Queue<int> dijkstra = new Queue<int>(); bool[] visits = new bool[m_MapWidth * m_MapHeight];//访问列表 int[] dis = new int[m_MapWidth * m_MapHeight];//所有点的移动消耗 for (int i = 0; i < dis.Length; i++)//初始为无穷大 { dis[i] = int.MaxValue; } int currNode = x + y * m_MapWidth + 1; dis[currNode - 1] = 0;//起点的移动消耗为0 dijkstra.Enqueue(currNode);//起点入队 while (dijkstra.Count > 0) { currNode = dijkstra.Dequeue(); m_QueuePoints.Enqueue(currNode); if (currNode == m_MapWidth * m_MapHeight)//目标节点(这里设置第一个点为起点,最后一个点为终点) { break; } visits[currNode - 1] = true; int currX = (currNode - 1) % m_MapWidth; int currY = (currNode - 1) / m_MapWidth; FindDestNode(currX, currY + 1, visits, dis[currNode - 1], dis, m_Nodes[currNode - 1]); FindDestNode(currX, currY - 1, visits, dis[currNode - 1], dis, m_Nodes[currNode - 1]); FindDestNode(currX - 1, currY, visits, dis[currNode - 1], dis, m_Nodes[currNode - 1]); FindDestNode(currX + 1, currY, visits, dis[currNode - 1], dis, m_Nodes[currNode - 1]); int minDisNode = -1; int tempDis = int.MaxValue; for (int j = 0; j < dis.Length; j++)//从所有节点中选择一个移动消耗最低且没有被访问过的点 { if (!visits[j] && dis[j] < tempDis) { minDisNode = j; tempDis = dis[j]; } } if (minDisNode >= 0) { dijkstra.Enqueue(minDisNode + 1);//入队 } } for(int i = 0; i < dis.Length; i++) { if (visits[i]) { Debug.Log(dis[i]); } } } private void FindDestNode(int x, int y, bool[] visits, int currDis, int[] dis, Node currNode) { if (x >= 0 && x < m_MapWidth && y >= 0 && y < m_MapHeight) { int index = x + y * m_MapWidth + 1; if (m_MapData[index - 1] != -1) { if (!visits[index - 1])//没有访问过 { dis[index - 1] = currDis + m_Map[index - 1];//累加移动消耗 } else if (dis[index - 1] > currDis + m_Map[index - 1]))//已访问,但当前路径的移动消耗更低 { dis[index - 1] = currDis + m_Map[index - 1];//更新移动消耗 } } } }以上代码虽然可以计算出从给定起点到终点的最少移动消耗,但仍然无法获取移动的路线,为了获得移动路线,要在此基础上增加回溯。
简单粗暴的方法就是使用一个链表把走过的路线链起来,等算法结束再从终点往起点回溯即可得到移动路线。
先声明一个链表
class Node { public int index; public Node parent; public Node(int index, Node parent) { this.index = index; this.parent = parent; } } m_Nodes = new Node[m_MapWidth * m_MapHeight];在处理移动消耗时把当前点和邻接节点进行链接
if (!visits[index - 1]) { dis[index - 1] = currDis + m_Map[index - 1]; m_Nodes[index - 1] = new Node(index, currNode); } else if (currDis + m_Map[index - 1] < dis[index - 1]) { dis[index - 1] = currDis + m_Map[index - 1]; m_Nodes[index - 1].parent = currNode; }在算法结束后增加回溯
Node node = m_Nodes[currNode - 1]; while (node != null) { m_QueuePath.Enqueue(node.index); node = node.parent; }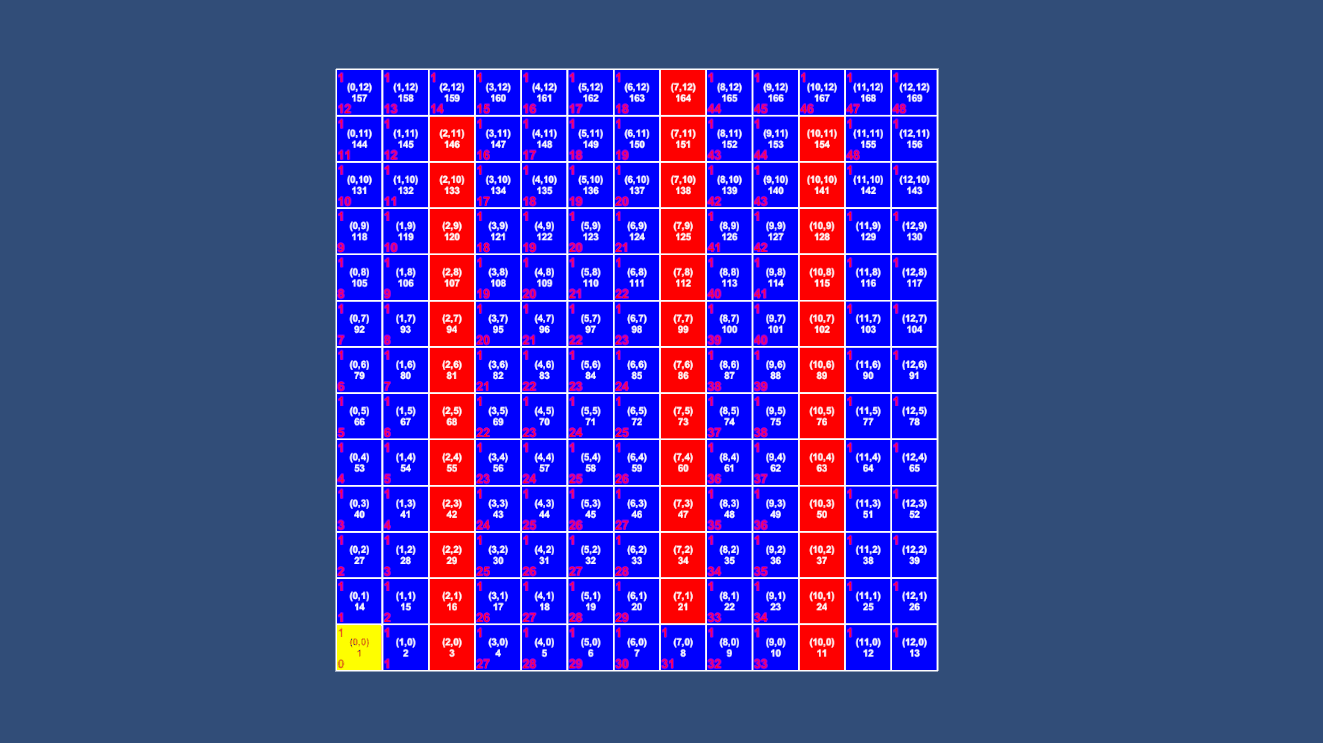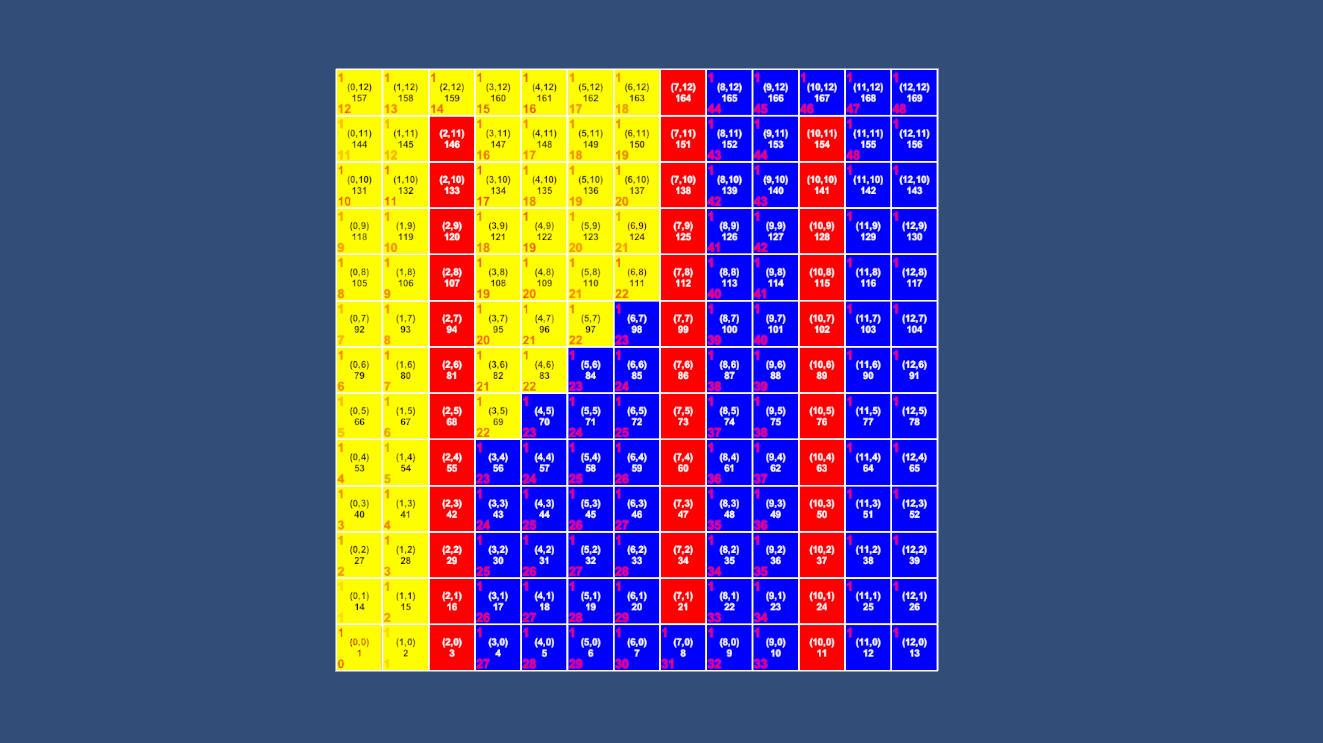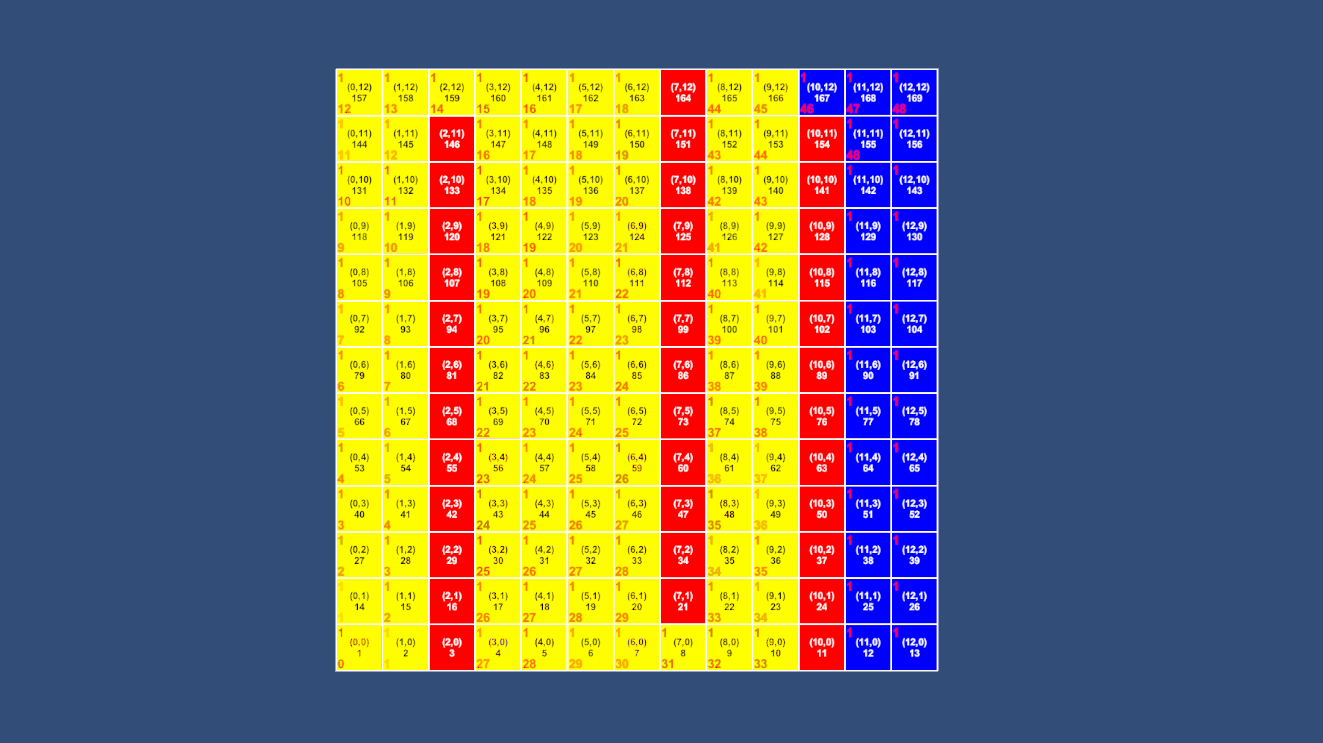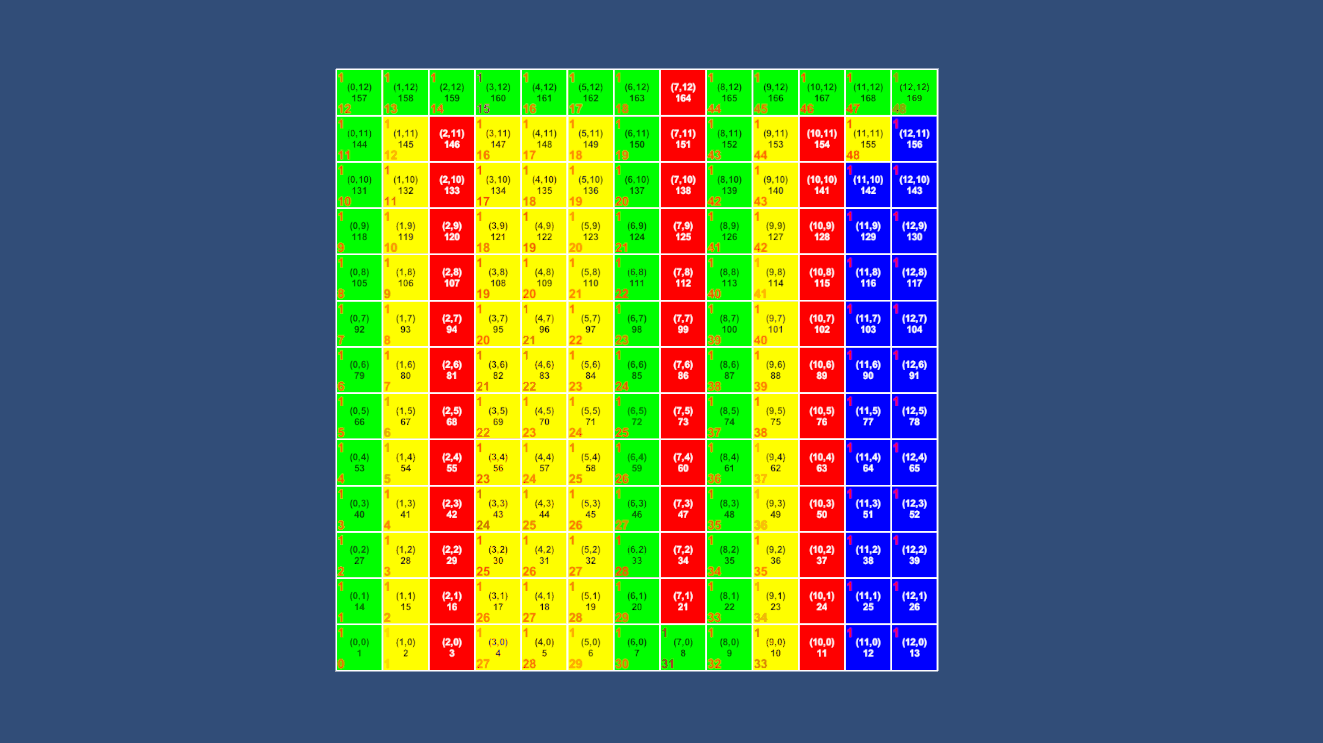
AStar(A*)算法
终于进入了本篇的正题。其实A*算法就是对Dijkstra算法的优化,在Dijkstra中每一步只计算移动消耗,这导致在向终点递进的过程中访问到许多无用节点,当地图中没有障碍时,甚至可能要把所有节点全访问到才得出结果。这显然不是一种最优解。

于是A*算法在Dijkstra算法的基础上引入一个当前点到终点的距离H,然后使F = 移动消耗G+距离H,也就是A*大名鼎鼎的F=G+H公式;再引入一个Open列表和Close列表,每次出队时把该节点从Open列表中移除并加入到Close列表,每次进行节点筛选时只从Open列表中选择一个F最小的节点入队。这使得A*算法能在访问更少节点的情况下找到通往目标点的最短路径。
算法的基本流程是:
- 把给定起始点入队,该点G = 0,计算该点到终点的距离H后使该点的F=G+H
- 把起始点加入Open列表
- 出队一个节点,并把该节点从Open列表中移除,再加入Close列表中
- 获取当前节点周围可以移动的邻接节点,并检测这些邻接节点是否在Open列表中
- 若已存在于Open列表,检测当前点移动到该邻接节点的移动消耗,是否比该邻接节点的移动消耗更低,并对该邻接节点的移动消耗G进行更新,重新计算该点的F=G+H
- 若不在则累加该邻接节点的移动消耗即G = G+1,计算该点到终点的距离H,使该点的F=G+H,然后加入到Open列表中
- 从Open列表中选择一个F值最低的节点入队
- 重复3,4,5,6,7直到Close列表中存在目标点
class Node : IComparable { public int index; //节点编号 public Node parent; public float f; public float g; public float h; public bool isOpen; public Node(int index, Node parent, float g, float h) { this.index = index; this.parent = parent; this.g = g; this.h = h; this.f = g + h; this.isOpen = true; } public int CompareTo(object obj) { if (obj == null) { return -1; } Node node = obj as Node; if (node.f == this.f) { return this.g > node.g ? -1 : 1; } return this.f > node.f ? 1 : -1; } } private void StartAStar(int xFrom, int yFrom, int xTo, int yTo) { Queue<Node> astar = new Queue<Node>(); List<Node> openList = new List<Node>(); int indexFrom = xFrom + yFrom * m_MapWidth + 1; int indexTo = xTo + yTo * m_MapWidth + 1; astar.Enqueue(new Node(indexFrom, null, 0, GetDistance(indexFrom, indexTo))); Node currNode = null; while (astar.Count > 0) { currNode = astar.Dequeue(); m_QueuePoints.Enqueue(currNode); if (currNode.index == indexTo) { break; } currNode.isOpen = false; if (!openList.Contains(currNode)) { openList.Add(currNode); } Tiled tiled = TiledMapMgr.instance.GetGridByIndex(currNode.index); tiled.txtRightBottom.text = currNode.h.ToString(); tiled.txtLeftTop.text = currNode.f.ToString(); int currX = (currNode.index - 1) % m_MapWidth; int currY = (currNode.index - 1) / m_MapWidth; FindDestNode(currX, currY + 1, xTo, yTo, currNode, openList); FindDestNode(currX, currY - 1, xTo, yTo, currNode, openList); FindDestNode(currX - 1, currY, xTo, yTo, currNode, openList); FindDestNode(currX + 1, currY, xTo, yTo, currNode, openList); Node minDistanceNode = openList.FindAll(node => node.isOpen).Min(); if (minDistanceNode != null) { astar.Enqueue(minDistanceNode); } } while (currNode != null) { m_QueuePath.Enqueue(currNode.index); currNode = currNode.parent; } } private void FindDestNode(int x, int y, int xTo, int yTo, Node currNode, List<Node> openList) { if (x >= 0 && x < m_MapWidth && y >= 0 && y < m_MapHeight) { int index = x + y * m_MapWidth + 1; int toIndex = xTo + yTo * m_MapWidth + 1; if (m_MapData[index - 1] != -1) { Node temp = openList.Find(obj => obj.index == index); if (temp == null) { temp = new Node(index, currNode, currNode.g + 1, GetDistance(index, toIndex)); openList.Add(temp); } else if (temp.isOpen && currNode.g + 1 + temp.h < temp.f) { temp.g = currNode.g + 1; temp.f = temp.g + temp.h; temp.parent = currNode; } } } } private int GetDistance(int from, int to)//计算起点到终点的距离,使用平方和即可 { int xFrom = (from - 1) % m_MapWidth; int yFrom = (from - 1) / m_MapWidth; int xTo = (to - 1) % m_MapWidth; int yTo = (to - 1) / m_MapWidth; int xDistance = Mathf.Abs(xTo - xFrom); int yDistance = Mathf.Abs(yTo - yFrom); return xDistance * xDistance + yDistance * yDistance; }这里当前点到目标点的距离使用了平方和来表示,也可以使用曼哈顿距离,即把x坐标和y坐标的差值直接相加:
distance = Mathf.Abs(xTo-xFrom) + Mathf.Abs(yTo-yFrom);下面就跑一下看看效果吧
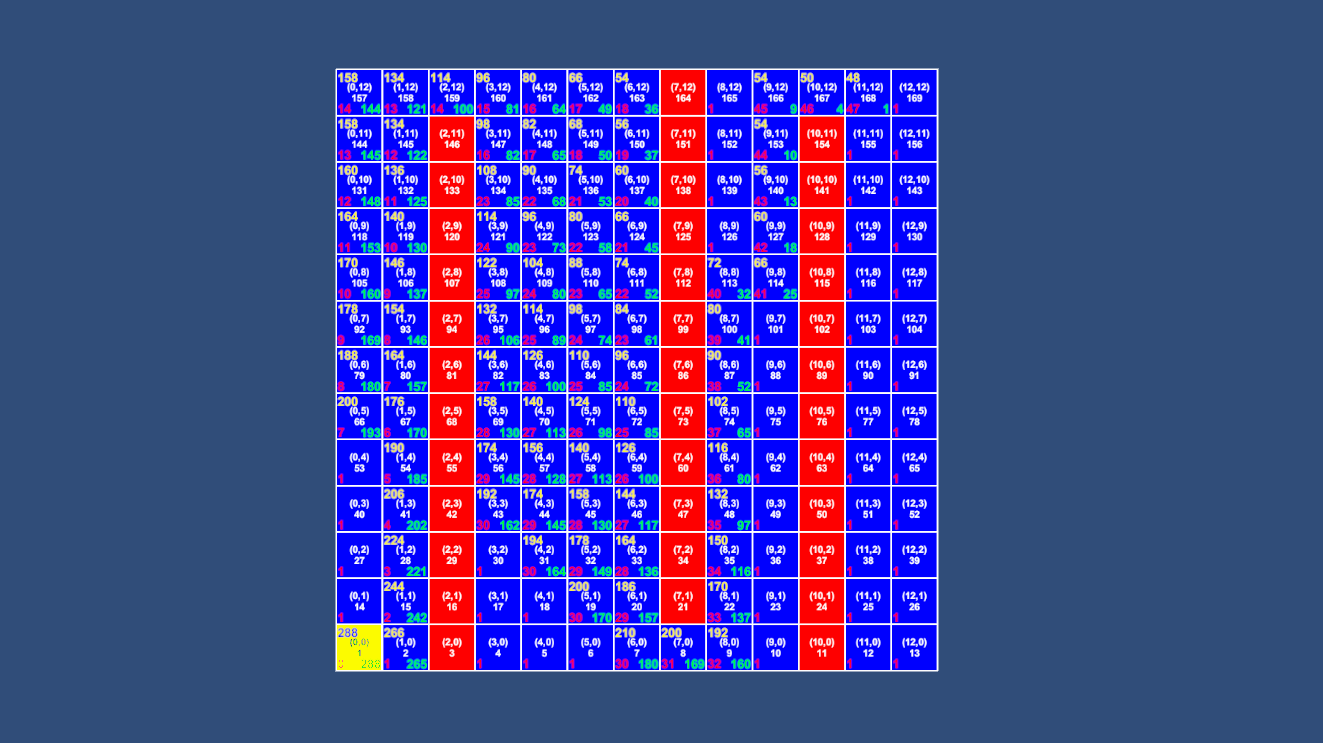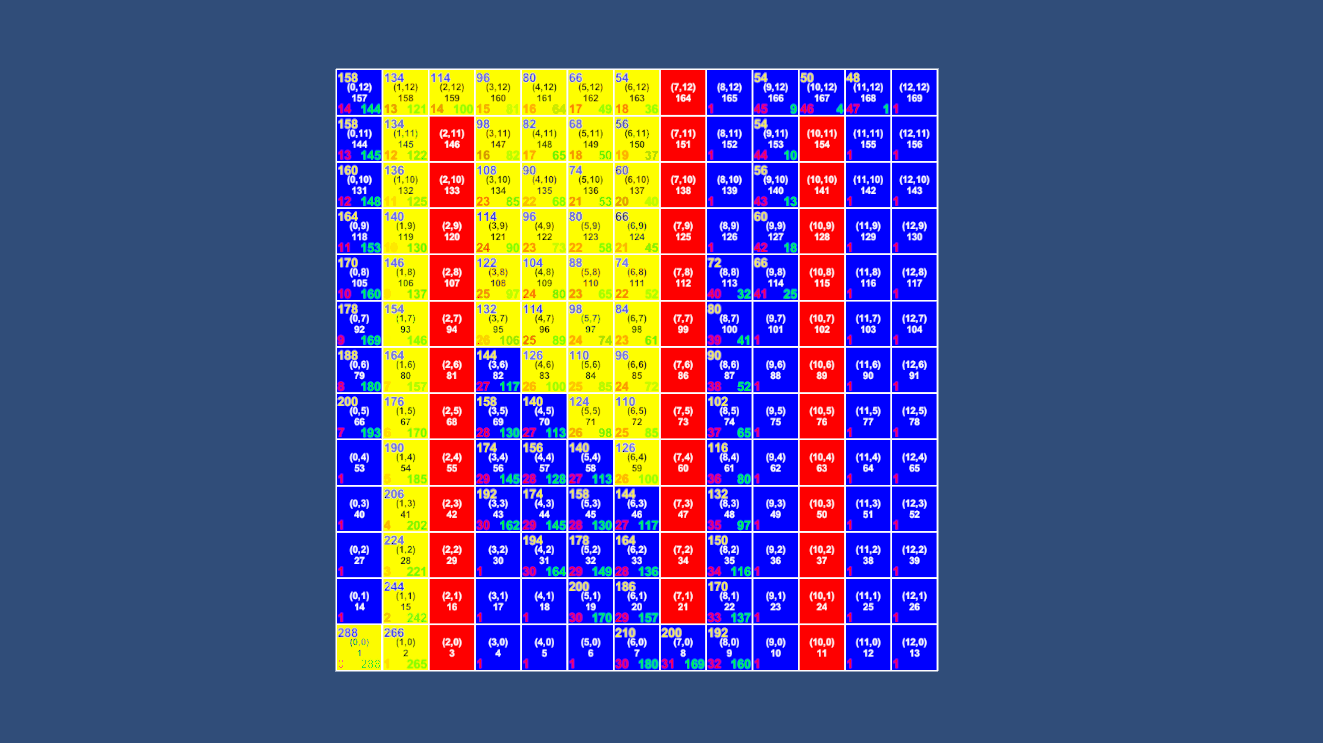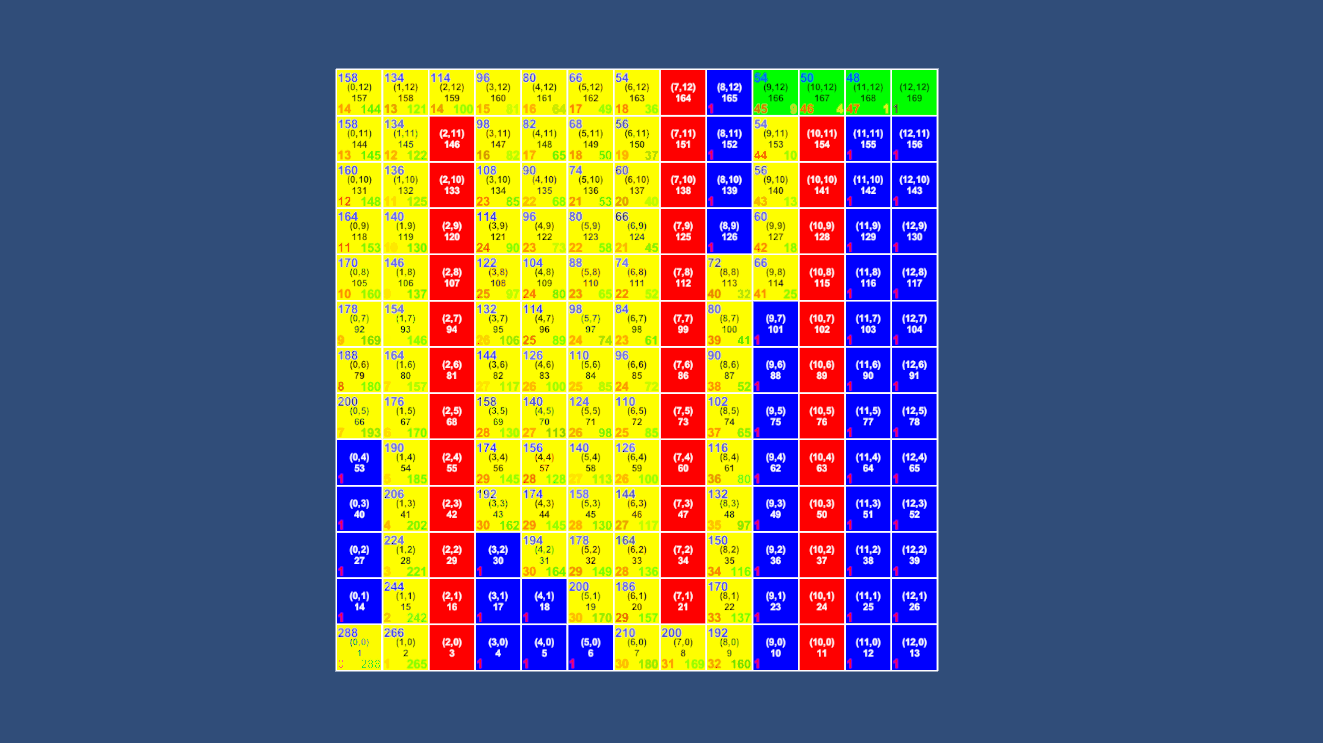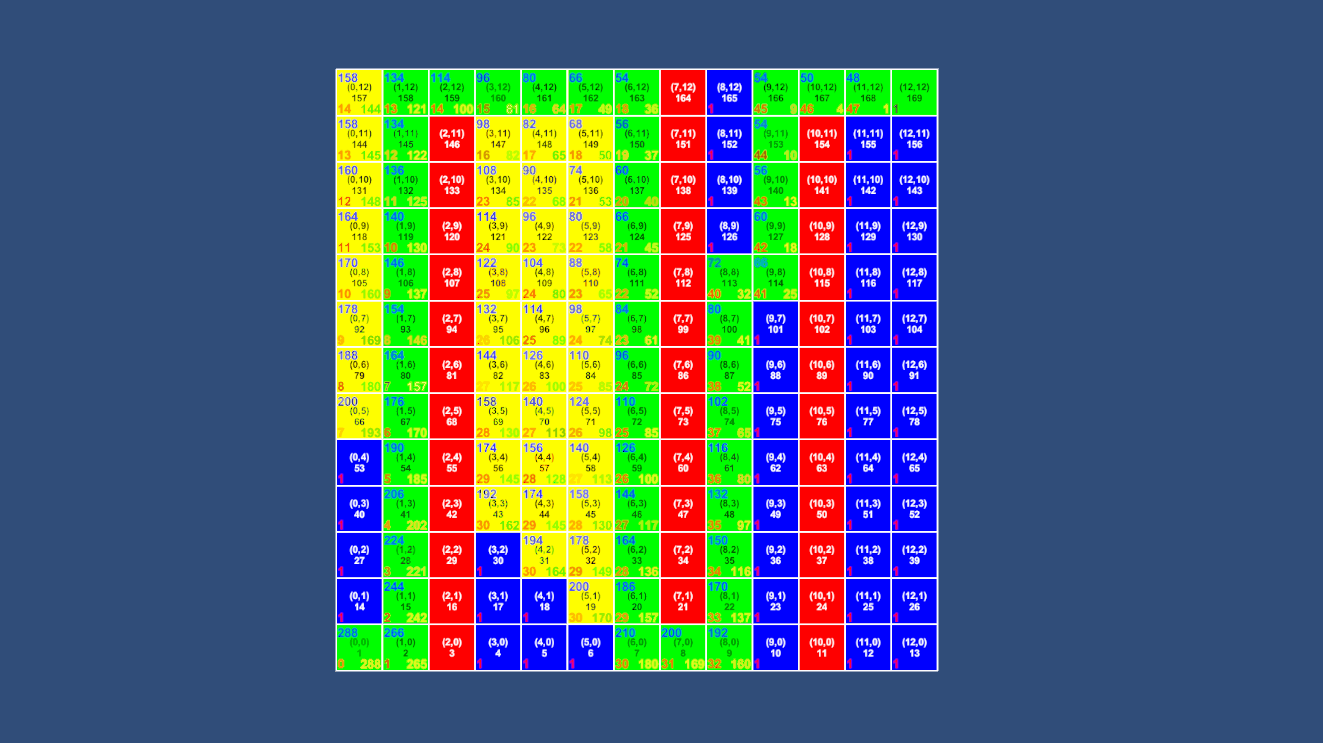
不难看出,同样的地图A*算法访问了更少的节点就找到了最短路径。

而去掉障碍后更是直接就找到了终点,效率提高了无数倍。
值得一提的是,当Open列表中存在相同F值的节点时,应选择G值最高的点,这符合A*算法始终朝终点扩张的思想。
结语
以上是对A*算法的一次探究和实现,所有代码和动态效果全部手撸,有错误或者不足欢迎指出。
工程地址:WuWu03/AStar: A*算法Untiy工程 (github.com) https://github.com/WuWu03/AStar
https://github.com/WuWu03/AStar
个人博客
一篇文章搞定AStar(A*)算法 | 幻想乡の红魔馆 (ming-e.space) https://ming-e.space/post/1d428483/
https://ming-e.space/post/1d428483/

