题型介绍
子数组系列动态规划问题长什么样
例题
解题步骤:
创建 dp 表以及确定 dp 表中所要填写位置的含义:
首先,根据写题经验,先确定出这道题应该使用的解题思路是 “以某一个位置为结尾进行分析”。
在这道题中,规定 dp[i] 表示以 i 位置为结尾的子数组中的最大和。
确定状态转移方程:
以 i 位置为结尾的子数组有两种情况。
① 子数组中只有自己,这时 dp[i] = nums[i]。
② 和前面的其他元素组成一个子数组,则可以理解为 以 i - 1 为结尾的最大子数组和 + nums[i] 本身。
所以,应该是上面两种情况的最大值。dp[i] = max(dp[i - 1] + nums[i], nums[i])。
初始化:
由于状态转移方程中,只涉及到 dp 表中的前一个位置,所以只需要将 dp[0] = nums[0],后续填表从 dp[1] 开始即可。
确定填表顺序:
根据状态转移方程可以看出应该从左向右依次填表。
确定返回值:
题目要求返回所有子数组中的最大和,所有的子数组可能以任何一个位置为结尾。
所以,可以在填表之后遍历 dp 表找出最大值,也可以在填表的过程中更新最大值,时间复杂度都是 O(N)。
代码:
class Solution { public: int maxSubArray(vector<int>& nums) { // 创建 dp 表 int n = nums.size(), ret = nums[0]; vector<int> dp(n); // 初始化 dp[0] = nums[0]; // 填表 for (int i = 1; i < n; i++) { dp[i] = max(nums[i], dp[i - 1] + nums[i]); ret = max(ret, dp[i]); } return ret; } };练习题
力扣 918. 环形子数组的最大和
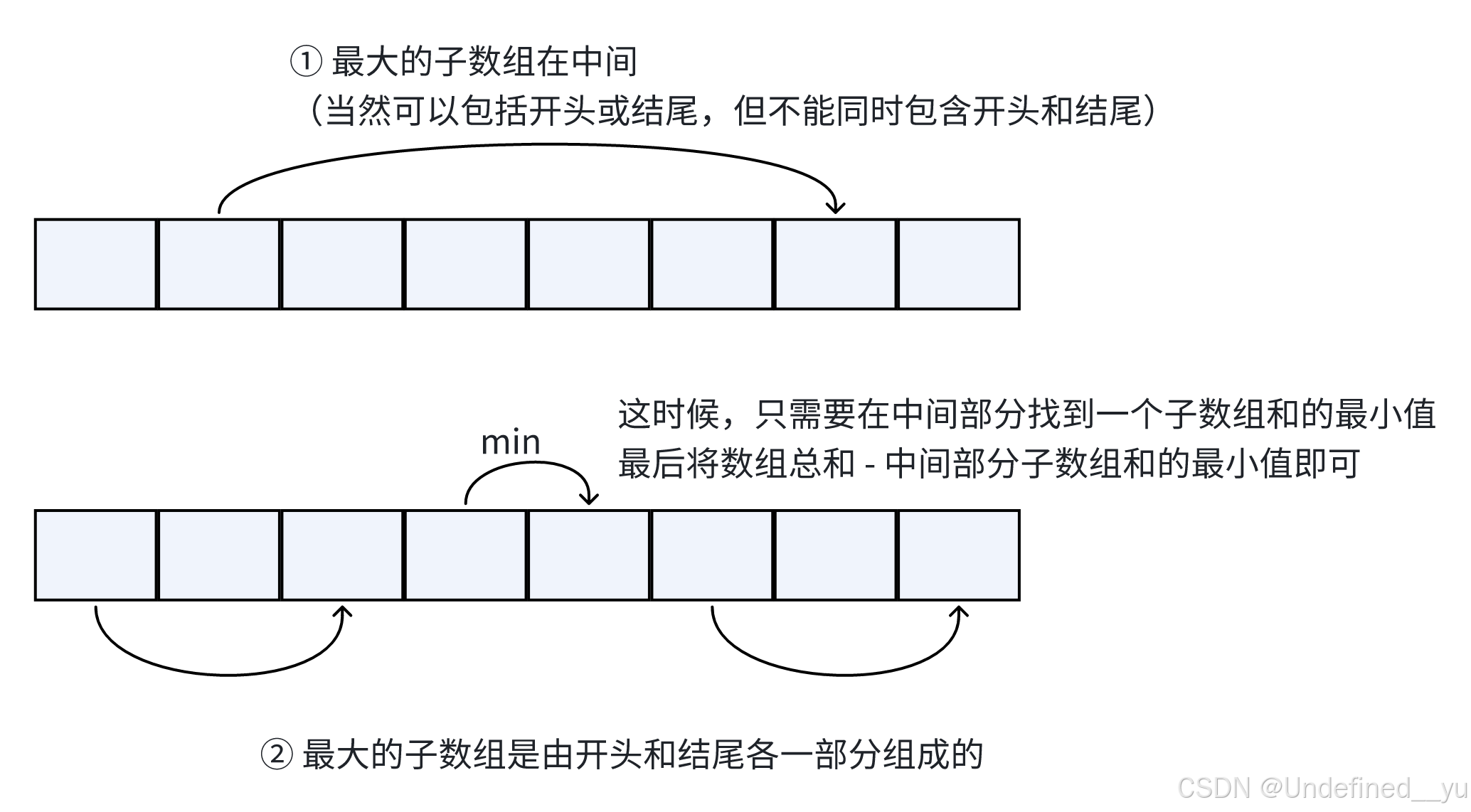
重点:环形子数组,跟例题的区别就是,这个数组是环形的。
环形意味着,一个子数组可以在数组中间,也可以由数组的开头和结尾组成。
在中间的情况就和例题一模一样,在两边的可以换一种思路。
解题步骤:
创建 dp 表以及确定 dp 表中所要填写位置的含义:
首先,根据写题经验,先确定出这道题应该使用的解题思路是 “以某一个位置为结尾进行分析”。
在这道题中,规定 Max[i] 表示以 i 位置为结尾的所有子数组中的最大和。
规定 Min[i] 表示以 i 位置为结尾的所有子数组中的最小和。
确定状态转移方程:
以 i 位置为结尾的子数组有两种情况。
① 子数组中只有自己,这时 dp[i] = nums[i]。
② 和前面的其他元素组成一个子数组,则可以理解为 以 i - 1 为结尾的最大子数组和 + nums[i] 本身。
所以,应该是上面两种情况的最大值或最小值。
Max[i] = max(Max[i - 1] + nums[i], nums[i])。Min[i] = min(Min[i - 1] + nums[i], nums[i])。
初始化:
由于状态转移方程中,只涉及到 dp 表中的前一个位置,所以只需要将 Max[0] = Min[0] = nums[0],将 Max 表中的其他值初始化为 INT_MIN,将 Min 表中的其他值初始化为 INT_MAX,后续填表从 dp[1] 开始即可。
确定填表顺序:
根据状态转移方程可以看出应该从左向右依次填表。
确定返回值:
题目要求返回所有子数组中的最大和,所有的子数组可能以任何一个位置为结尾。
所以,应该找出 Max 中的最大值和 Min 中的最小值。然后返回 Max 中的最大值以及原数组和减去 Min 中的最小值中更大的那一个。
这里注意,如果给出的数组中全是负数,则数组总和会等于 Min 中的最小值,这时应该返回的是原数组中最小的那个元素,也就是 Max 中的最大值。
代码:
class Solution { public: int maxSubarraySumCircular(vector<int>& nums) { int n = nums.size(), sum = 0, big = nums[0], litter = nums[0]; for (int num : nums) sum += num; // 创建 dp 表 vector<int> Max(n, INT_MIN), Min(n, INT_MAX); // 初始化 Max[0] = Min[0] = nums[0]; // 填表 for (int i = 1; i < n; i++) { Max[i] = max(Max[i - 1] + nums[i], nums[i]); Min[i] = min(Min[i - 1] + nums[i], nums[i]); big = max(big, Max[i]); litter = min(litter, Min[i]); } return sum == litter ? big : max(big, sum - litter); } };力扣 152. 乘积最大子数组
这道题跟上面那道题有个不同之处,这道题用乘法,上面那道题用加法。
乘法就涉及到某一个位置的元素是正数、负数还是 0 的情况,三种情况得到的结果是不一样的。
如果某个位置的元素为 0,不管子数组中只有自己还是包括其他元素,乘积都是 0。
如果某个位置的元素为正数,那么它乘以一个负数就会变小,乘以一个正数就会变大。
如果某个位置的元素为负数,那么它乘以一个正数就会变小,乘以一个负数就会变大。
所以,针对一个正数,当子数组中还包含其他数的时候,应该用它乘以以前一个位置为结尾的所有子数组中乘积的最大值。
针对一个负数,当子数组中还包含其他数的时候,应该用它乘以以前一个位置为结尾的所有子数组中乘积的最小值。
所以需要两个 dp 表,因为一个 dp 表不足以表示出所有的状态。
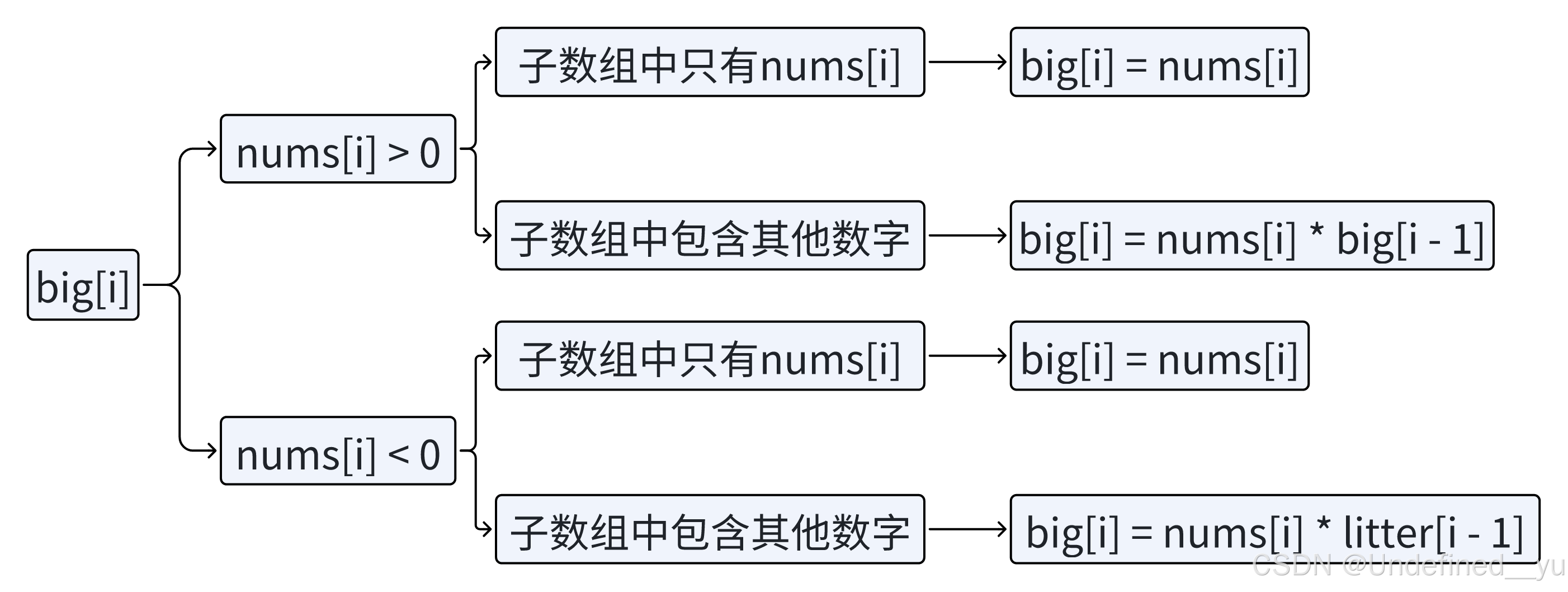
big[i] 表示以 i 位置为结尾(包含 nums[i])的所有乘积为正数的子数组中的最大乘积。
litter[i] 表示以 i 位置为结尾(包含 nums[i])的所有乘积为负数的子数组中的最小乘积。
当 nums[i] > 0 时,乘以一个最大的正数得到的就是以 i 位置为结尾的子数组中的最大乘积,或者子数组中只有自己。
当 nums[i] < 0 时,乘以一个最小的负数得到的就是以 i 位置为结尾的子数组中的最大乘积,或者子数组中只有自己。
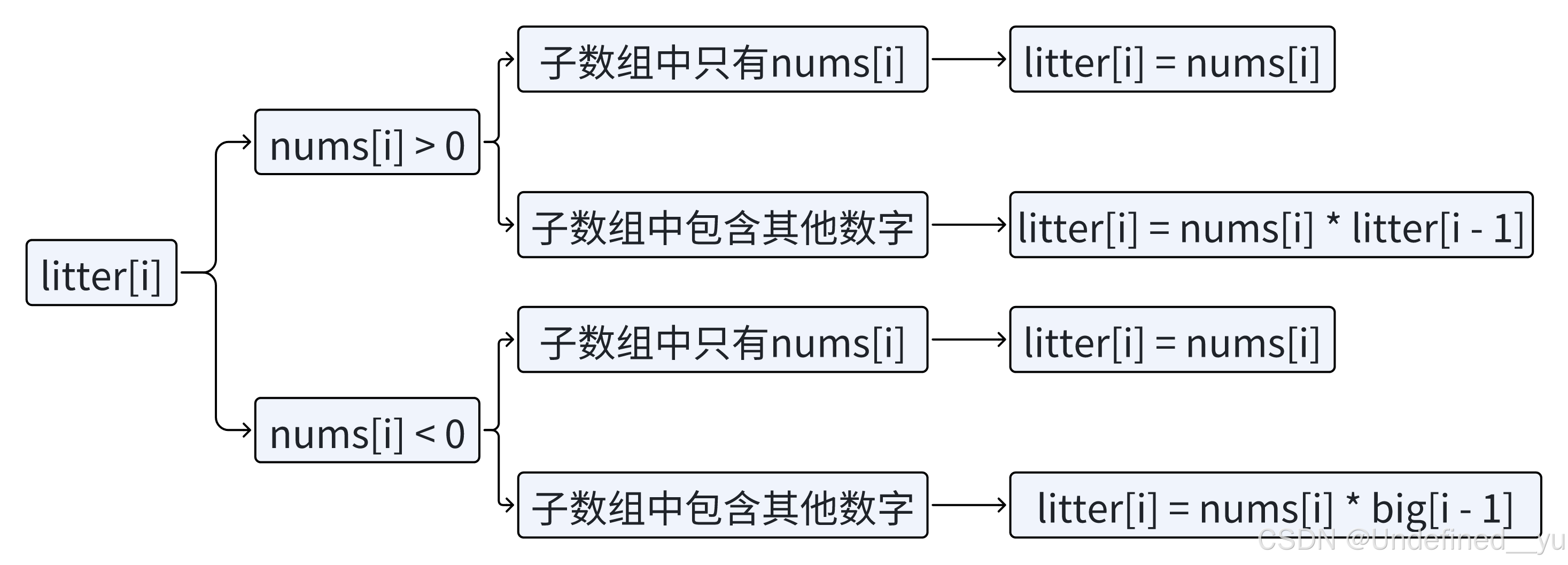
当 nums[i] > 0 时,乘以一个最小的负数得到的就是以 i 位置为结尾的子数组中的最小乘积,或者子数组中只有自己。
当 nums[i] < 0 时,乘以一个最大的正数得到的就是以 i 位置为结尾的子数组中的最小乘积,或者子数组中只有自己。
以上情况在 nums[i] = 0 的时候也是成立的,所以不用单独拿出来讨论。
代码:
class Solution { public: int maxProduct(vector<int>& nums) { // 创建 dp 表 + 初始化 int n = nums.size(); vector<long long> big(n, INT_MIN), litter(n, INT_MAX); big[0] = litter[0] = nums[0]; // 填表 for (int i = 1; i < n; i++) { big[i] = max(nums[i], max(nums[i] * big[i - 1], nums[i] * litter[i - 1])); litter[i] = min(nums[i], min(nums[i] * litter[i - 1], nums[i] * big[i - 1])); } return *max_element(big.begin(), big.end()); } };力扣 1567. 乘积为正数的最长子数组长度
这道题也需要分为乘积为正数和负数两个 dp 表。
f[i] 表示以 i 位置为结尾的,乘积为正数的,最长子数组的长度。
g[i] 表示以 i 位置为结尾的,乘积为负数的,最长子数组的长度。
所以,当 nums[i] > 0 时,f[i] = f[i - 1] + 1。因为如果前一个也是正数,则再多一个正数,长度就 +1。
g[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1。因为如果前一个为负数,则正数乘以负数还是负数,所以 +1,但要注意以前一个位置为结尾的子数组中是否有乘积为负数的子数组,所以加了一个判断。
当 nums[i] < 0 时,f[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1。因为负数只有乘以负数才是正数,同样也需要注意以前一个位置为结尾的子数组中是否有乘积为负数的子数组。
g[i] = f[i - 1] + 1。因为负数乘以正数还是负数,因为 dp 表初始化为 0,所以不用判断。
代码:
class Solution { public: int getMaxLen(vector<int>& nums) { // 创建 dp 表 int n = nums.size(); vector<int> f(n), g(n); // 初始化 if (nums[0] > 0) f[0] = 1; else if (nums[0] < 0) g[0] = 1; // 填表 for (int i = 1; i < n; i++) { if (nums[i] > 0) { f[i] = f[i - 1] + 1; g[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1; } else if (nums[i] < 0) { f[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1; g[i] = f[i - 1] + 1; } } return *max_element(f.begin(), f.end()); } };力扣 413. 等差数列划分
这道题算是比较简单的,只需要从前往后判断,相邻的三个元素能不能构成等差数组即可。
但是返回值应该是,以每一个位置为结尾的所有等差子数组的总数的和。
代码:
class Solution { public: int numberOfArithmeticSlices(vector<int>& nums) { int n = nums.size(), ret = 0; vector<int> dp(n); for (int i = 2; i < n; i++) { dp[i] = nums[i] - nums[i - 1] == nums[i - 1] - nums[i - 2] ? dp[i - 1] + 1 : 0; ret += dp[i]; } return ret; } };力扣 978. 最长湍流子数组
这道题其实是跟上一道题一样的。
只是需要注意,每一个单个的元素都是一个长度为一的湍流子数组。
任意两个相邻的且不相等的元素,都可以构成一个长度为二的湍流子数组。
如果相邻的三个元素可以构成湍流子数组,则只需要考虑前一个位置湍流子数组中元素的个数,然后 +1 即可。
代码:
class Solution { public: int maxTurbulenceSize(vector<int>& arr) { int n = arr.size(); if (n == 1) return 1; vector<int> dp(n); dp[0] = 1; dp[1] = arr[1] == arr[0] ? 1 : 2; int ret = dp[1]; for (int i = 2; i < n; i++) { if (arr[i] == arr[i - 1]) dp[i] = 1; else if ((arr[i] > arr[i -1] && arr[i - 1] < arr[i - 2]) || (arr[i] < arr[i - 1] && arr[i - 1] > arr[i - 2])) dp[i] = dp[i - 1] + 1; else dp[i] = 2; ret = max(ret, dp[i]); } return ret; } };力扣 139. 单词拆分
这道题仍然可以用 dp[i] 来表示字符串 s 中,以 i 位置为结尾的字符串,是否满足可以由 wordDict 中的单词组成的条件,即 dp[i] 中是一个 bool 值。
但是,由 dp[i] 却无法推出一个可以正确表示 dp[i + 1] 的状态转移方程。
所以,可以换一种思路。

所以,对于以 i 位置为结尾的字符串,还需要多加一层循环,用来找到合适的 j 以使 0~j 和 j~i 这两段子字符串都满足条件。
代码:
class Solution { public: bool wordBreak(string s, vector<string>& wordDict) { unordered_set<string> hash; for (string word : wordDict) hash.insert(word); int n = s.size(); vector<bool> dp(n + 1); dp[0] = true; s = ' ' + s; for (int i = 1; i <= n; i++) { for (int j = i; j >= 1; j--) { if (dp[j - 1] && hash.count(s.substr(j, i - j + 1))) { dp[i] = true; break; } } } return dp[n]; } };力扣 467. 环绕字符串中唯一的子字符串
这道题用一层循环足以。
只需从前往后依次判断,两个相邻的字符相差是不是 1,或者前一个是 z,后一个是 a 也满足条件。
如果满足条件,则 dp[i] = dp[i - 1] + 1。dp[i] 表示以 i 位置为结尾的子字符串中满足条件的个数。
但是,有一个问题,题目要求返回的应该是所有符合条件的子字符串的和,如果直接将 dp 表中的每一个位置相加,结果会有重复。
所以,可以借助一个哈希表来记录以每一个字符为结尾的,满足条件的子字符串的个数。
最后,再依次相加即可。
代码:
class Solution { public: int findSubstringInWraproundString(string s) { int n = s.size(), ret = 0; vector<int> dp(n, 1); for (int i = 1; i < n; i++) { if (s[i] - s[i - 1] == 1 || (s[i - 1] == 'z' && s[i] == 'a')) dp[i] = dp[i - 1] + 1; } vector<int> hash(26); for (int i = 0; i < n; i++) hash[s[i] - 'a'] = max(hash[s[i] - 'a'], dp[i]); for (int num : hash) ret += num; return ret; } };