阅读量:0
决策树可解释性分析
决策树是一种广泛使用的机器学习算法,以其直观的结构和可解释性而闻名。在许多应用场景中,尤其是金融、医疗等领域,模型的可解释性至关重要。本文将从决策路径、节点信息、特征重要性等多个方面分析决策树的可解释性,并提供相应的代码实现。
决策树可解释性分析
1. 决策树的基本结构
决策树以树形结构表示模型的决策过程。每个节点代表一个特征的测试,每条边代表测试结果的分支,叶子节点代表最终的预测结果。决策树的可解释性主要来源于其简单直观的结构,用户可以通过观察树的分裂过程理解模型的决策依据。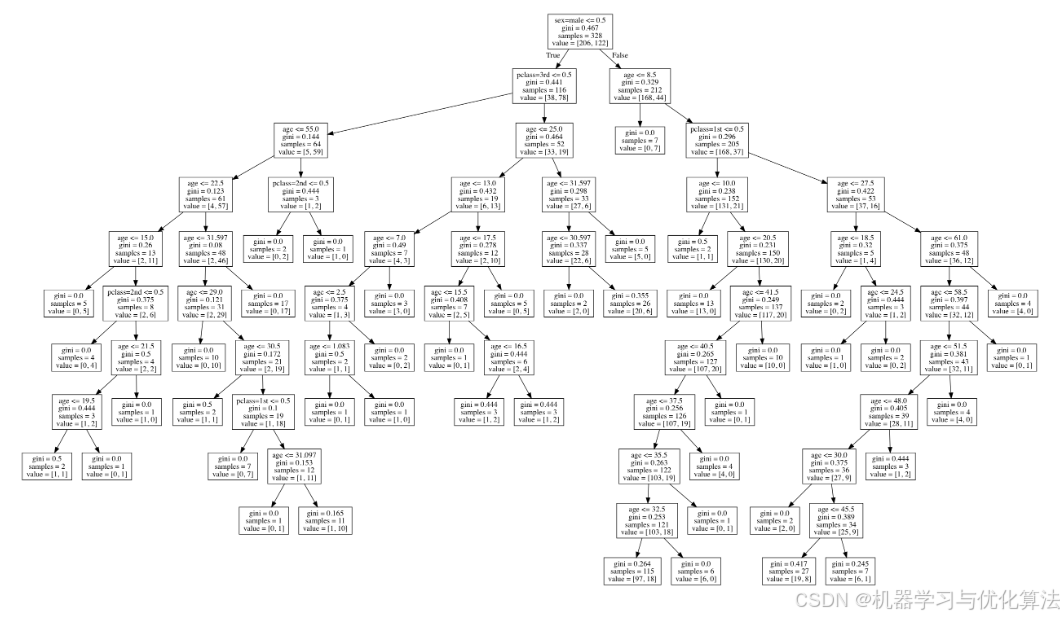
2. 决策路径
2.1 决策路径的概念
决策路径是指从根节点到达某个叶子节点的路径。通过分析决策路径,我们可以理解模型在特定样本上的预测依据。例如,在某个节点上,模型可能会根据特征A的值进行分裂,然后根据特征B的值进一步分裂,最终得出分类结果。
2.2 决策路径的可解释性
- 透明性:决策树的每一步决策都可以通过简单的条件判断表示,用户可以直观地理解模型的决策过程。
- 示例分析:通过分析具体样本的决策路径,可以清晰地看到哪些特征对最终预测产生了影响。
3. 节点信息
每个节点的信息可以提供关于模型决策的更多细节。节点信息通常包括以下内容:
- 特征名称:用于分裂的特征。
- 分裂阈值:特征的分裂条件。
- 样本数量:在该节点上的样本数量。
- 类别分布:在该节点上各类别的样本分布。
3.1 节点信息的可解释性
- 特征重要性:通过查看每个节点的信息,可以评估特征在模型中的重要性。例如,某个特征在多个节点中频繁出现,说明该特征对模型决策的影响较大。
- 样本分布:节点的样本数量和类别分布可以帮助我们理解模型在特定条件下的决策依据,从而识别潜在的偏差。
4. 特征重要性
特征重要性是评估模型可解释性的重要指标。决策树模型可以计算每个特征对最终预测的贡献程度。
4.1 特征重要性的计算
特征重要性可以通过以下方式计算:
- 基于分裂增益:每次分裂所带来的信息增益可以累积到特征上,最终得到特征的重要性评分。
- 基于节点不纯度:使用基尼指数或信息增益等指标,计算每个特征在树中分裂的贡献。
5. 代码实现
下面是一个简单的代码实现,展示如何使用scikit-learn构建决策树并分析其可解释性。
5.1 安装依赖
确保已安装scikit-learn和matplotlib库:
pip install scikit-learn matplotlib import numpy as np import pandas as pd import matplotlib.pyplot as plt from sklearn.datasets import load_iris from sklearn.tree import DecisionTreeClassifier, export_text, plot_tree # 加载数据 data = load_iris() X = data.data y = data.target feature_names = data.feature_names # 创建决策树模型 tree_model = DecisionTreeClassifier(max_depth=3, random_state=42) tree_model.fit(X, y) # 1. 决策路径示例 sample_index = 0 # 选择第一个样本 decision_path = tree_model.decision_path(X[sample_index].reshape(1, -1)) print(f"样本 {sample_index} 的决策路径:") print(decision_path) # 2. 节点信息 tree_rules = export_text(tree_model, feature_names=feature_names) print("\n决策树规则:") print(tree_rules) # 3. 特征重要性 importance = tree_model.feature_importances_ feature_importance_df = pd.DataFrame({ 'Feature': feature_names, 'Importance': importance }).sort_values(by='Importance', ascending=False) print("\n特征重要性:") print(feature_importance_df) # 4. 可视化决策树 plt.figure(figsize=(12, 8)) plot_tree(tree_model, feature_names=feature_names, filled=True) plt.title("决策树可视化") plt.show() 