阅读量:0
本文主要介绍了如何判断链表有环的问题,并进行了延伸: 如果链表有环如何求出环的长度,入环节点... ...嗯,点个赞总可以不!!!
目录
5.1.1 有一个单向链表,链表中可能出现“环”,那么如何判断该列表是否为有环链表呢?
5.1如何判断链表有环
5.1.1 有一个单向链表,链表中可能出现“环”,那么如何判断该列表是否为有环链表呢?
首先创建两个指针p1、p2(在Python中就是两个对象引用),让它们同时指向这个链表的头结点。然后开始一个大循环,在循环体中,让指针p1每次向后移动1个节点,让指针p2每次向后移动2个节点,然后比较两个指针指向的节点是否相同。如果相同,则可以判断出链表有环,如果不同,则继续进行下一次循环。
节点数量为n,则时间复杂度为O(n),空间复杂度为O(1)。
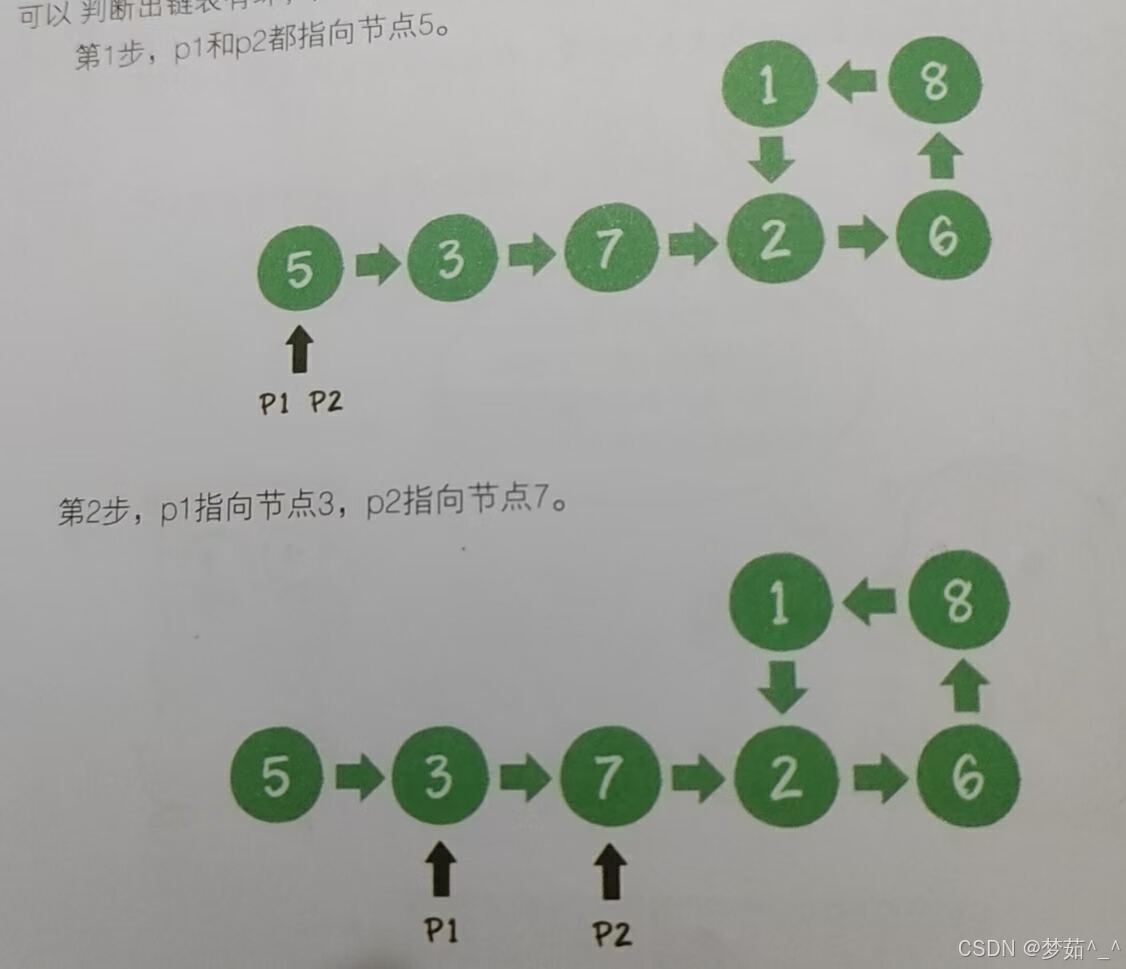
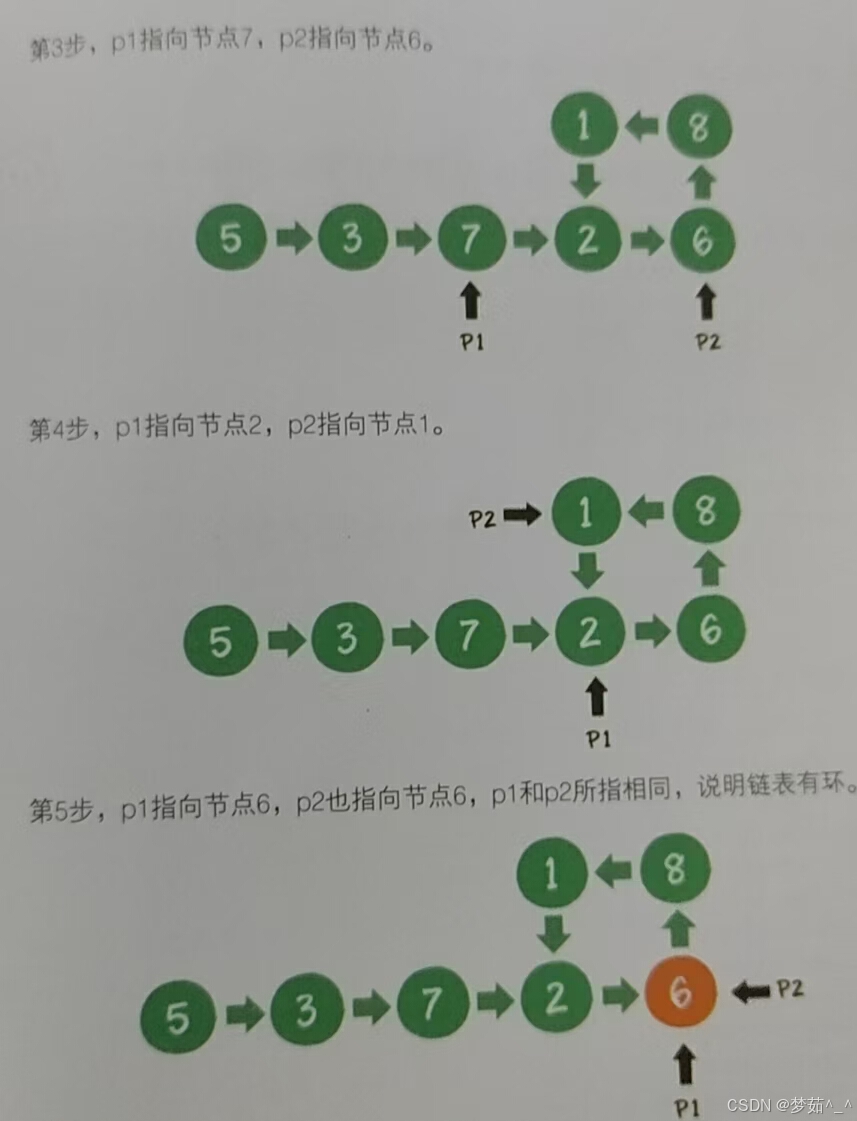
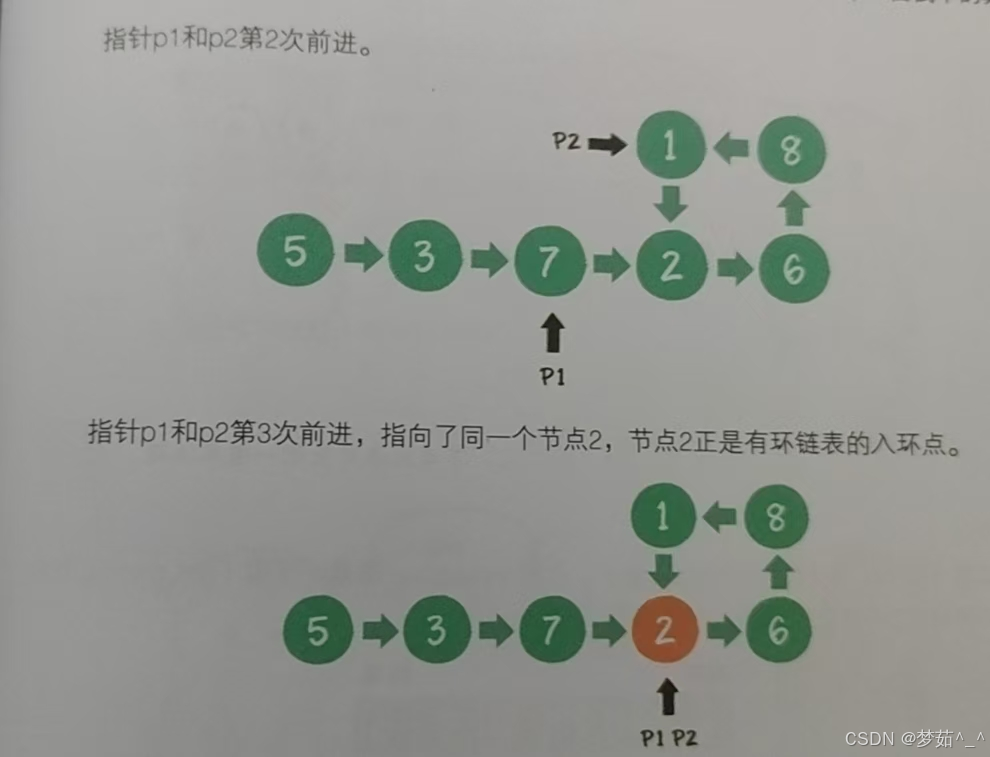
# 判断链表是否有环问题 class Node: def __init__(self,data): self.data = data self.next = None def is_cycle(head): p1 = head p2 = head while p2 is not None and p2.next is not None: p1 = p1.next p2 = p2.next.next if p1 == p2: return True return False node1 = Node(5) node2 = Node(3) node3 = Node(7) node4 = Node(2) node5 = Node(6) node1.next = node2 node2.next = node3 node3.next = node4 node4.next = node5 node5.next = node2 print(is_cycle(node1))5.1.2 如果链表有环,如何求出环的长度
两个指针首次相遇,证明链表有环,让两个指针从相遇点继续前进,并统计循环的次数,直到两个指针第二次相遇。此时,统计出来的前进的次数就是环长。
P1走一步,P2走两步,所以再次相遇的时候,P2走的路程是P1的两倍,多走了整整一圈。
因此,环长 = 每一次速度差 x 前进次数 = 前进次数
5.1.3 如果链表有环,如何求出入环节点
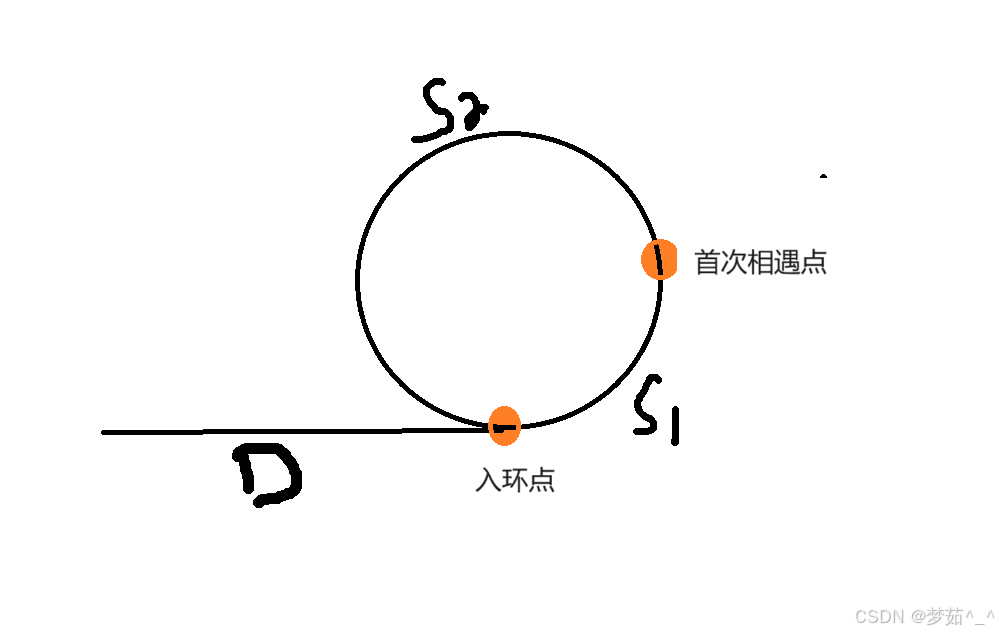
当两个指针首次相遇时,各自走的路程是多少呢?
指针P1一次走一步,所走的距离是D+S1
指针P2一次走两步,多走了n(n>=1)圈,所走的距离是D+S1+n(S1+S2)
因为P2的速度是P1的两倍,所以走的路程也应该是P1的两倍:
2(D+S1) = D+S1+n(S1+S2) ——> D = (n-1)(S1+S2)+S2
方法就是,把其中一个指针放回到头结点位置,另一个指针保持在首次相遇点,两个指针都每次向前走一步。那么,他们最终相遇的节点,就是入环节点。