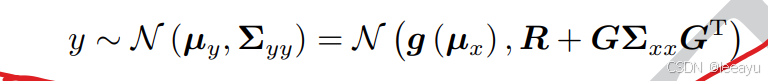文章目录
1 概率密度函数 PDF
请注意公式⾥⾯的 p(x) 是概率密度(probability density)⽽不是概率(probability)。
∫ a b p ( x ) d x = 1 \int_a^b p(x) \mathrm{d} x=1 ∫abp(x)dx=1
PDF的积分为概率:
Pr ( c ≤ x ≤ d ) = ∫ c d p ( x ) d x \operatorname{Pr}(c \leq x \leq d)=\int_c^d p(x) \mathrm{d} x Pr(c≤x≤d)=∫cdp(x)dx
条件概率, x ∈ [ a , b ] x \in [a, b] x∈[a,b] 在 y ∈ [ c , d ] y \in [c, d] y∈[c,d]的条件下的PDF如下
( ∀ y ) ∫ a b p ( x ∣ y ) d x = 1 (\forall y) \quad \int_a^b p(x \mid y) \mathrm{d} x=1 (∀y)∫abp(x∣y)dx=1
x, y 联合概率密度函数(joint probability densities)
p ( x , y ) p(\boldsymbol{x}, \boldsymbol{y}) p(x,y)
2 贝叶斯推断 Bayesian Inference
2.1 贝叶斯公式 Bayes’ Rule
关键的就是两条公式
p ( x , y ) = p ( x ∣ y ) p ( y ) = p ( y ∣ x ) p ( x ) p(\boldsymbol{x}, \boldsymbol{y})=p(\boldsymbol{x} \mid \boldsymbol{y}) p(\boldsymbol{y})=p(\boldsymbol{y} \mid \boldsymbol{x}) p(\boldsymbol{x}) p(x,y)=p(x∣y)p(y)=p(y∣x)p(x)
变形之后就是贝叶斯公式,这条公式在状态估计中会被反复使用,是最核心的公式,公式本身没有任何假设。
p ( x ∣ y ) = p ( y ∣ x ) p ( x ) p ( y ) p(\boldsymbol{x} \mid \boldsymbol{y})=\frac{p(\boldsymbol{y} \mid \boldsymbol{x}) p(\boldsymbol{x})}{p(\boldsymbol{y})} p(x∣y)=p(y)p(y∣x)p(x)
关于这个公式,每个PDF有个通俗的叫法
- P(x|y) Posteriori PDF
- P(y|x) 传感器观测模型,Measurement PDF,
- P(x) Prior PDF
贝叶斯公式的直观理解:使用先验PDF和观测PDF来推断后验的PDF,有了后验的PDF我们就知道当前应该选择的最佳估计值,以及估计值对应的不确定程度(方差)。
2.2 贝叶斯推断Bayesian Inference
- 输入:先验P(x), 观测P(y|x)
- 输出:后验P(x|y)
将 P(y) 展开得到
p ( x ∣ y ) = p ( y ∣ x ) p ( x ) p ( y ) = p ( y ∣ x ) p ( x ) ∫ p ( y ∣ x ) p ( x ) d x p(\boldsymbol{x} \mid \boldsymbol{y})= \frac{p(\boldsymbol{y} \mid \boldsymbol{x}) p(\boldsymbol{x})}{p(\boldsymbol{y})} =\frac{p(\boldsymbol{y} \mid \boldsymbol{x}) p(\boldsymbol{x})}{\int p(\boldsymbol{y} \mid \boldsymbol{x}) p(\boldsymbol{x}) \mathrm{d} \boldsymbol{x}} p(x∣y)=p(y)p(y∣x)p(x)=∫p(y∣x)p(x)dxp(y∣x)p(x)
P(y)的计算方式就是把x通过积分来边缘化掉的。关于边缘化可以参看文章
2.3 PDF连续状态的特性:矩 Moments
- 一阶矩:expectation/mean,期望
μ = E [ x ] = ∫ x p ( x ) d x \boldsymbol{\mu}=E[\boldsymbol{x}]=\int \boldsymbol{x} p(\boldsymbol{x}) \mathrm{d} \boldsymbol{x} μ=E[x]=∫xp(x)dx - 二阶矩:covariance 协方差矩阵
Σ = E [ ( x − μ ) ( x − μ ) T ] \boldsymbol{\Sigma}=E\left[(\boldsymbol{x}-\boldsymbol{\mu})(\boldsymbol{x}-\boldsymbol{\mu})^{\mathrm{T}}\right] Σ=E[(x−μ)(x−μ)T] - 三阶矩:skewness 偏度
- 四阶矩:kurtosis 峰度
Moments的期望和方差是一个PDF的关键特征,理论上可以定义无限阶次矩,通过无限阶次矩来恢复PDF。
通常在状态估计中我们只用期望和协方差来近似描述一个PDF最佳估计值所在的点。
特别的对于高斯分布,只是用期望和协方差便可以完整地描述整个PDF。
2.4 PDF离散状态的描述:均值和方差
对应于连续状态PDF的期望和协方差
μ meas = 1 N ∑ i = 1 N x i , meas Σ meas = 1 N − 1 ∑ i = 1 N ( x i , meas − μ meas ) ( x i , meas − μ meas ) T \begin{aligned} \boldsymbol{\mu}_{\text {meas }} & =\frac{1}{N} \sum_{i=1}^N \boldsymbol{x}_{i, \text { meas }} \\ \boldsymbol{\Sigma}_{\text {meas }} & =\frac{1}{N-1} \sum_{i=1}^N\left(\boldsymbol{x}_{i, \text { meas }}-\boldsymbol{\mu}_{\text {meas }}\right)\left(\boldsymbol{x}_{i \text {, meas }}-\boldsymbol{\mu}_{\text {meas }}\right)^{\mathrm{T}} \end{aligned} μmeas Σmeas =N1i=1∑Nxi, meas =N−11i=1∑N(xi, meas −μmeas )(xi, meas −μmeas )T
2.5 归一化积:融合对同⼀个随机变量的多次估计
- 输入: P(x|y1), P(x|y2), P(x|y3), …, P(x|yn)
- 输出:P(x|y1, y2, y3, …, yn)
- 假设:y1,y2,y3, …, yn相互独立

根据贝叶斯理论,归⼀化积可⽤于融合对同⼀个随机变量的多次估计。
x为估计变量,y1,y2是两次独立的测量,
p ( y 1 , y 2 ∣ x ) = p ( y 1 ∣ x ) p ( y 2 ∣ x ) = p ( x ∣ y 1 ) p ( y 1 ) p ( x ) p ( x ∣ y 2 ) p ( y 2 ) p ( x ) p\left(\boldsymbol{y}_1, \boldsymbol{y}_2 \mid \boldsymbol{x}\right)=p\left(\boldsymbol{y}_1 \mid \boldsymbol{x}\right) p\left(\boldsymbol{y}_2 \mid \boldsymbol{x}\right)=\frac{p\left(\boldsymbol{x} \mid \boldsymbol{y}_1\right) p\left(\boldsymbol{y}_1\right)}{p(\boldsymbol{x})} \frac{p\left(\boldsymbol{x} \mid \boldsymbol{y}_2\right) p\left(\boldsymbol{y}_2\right)}{p(\boldsymbol{x})} p(y1,y2∣x)=p(y1∣x)p(y2∣x)=p(x)p(x∣y1)p(y1)p(x)p(x∣y2)p(y2)
整理得到
p ( x ∣ y 1 , y 2 ) = η p ( x ∣ y 1 ) p ( x ∣ y 2 ) η = p ( y 1 ) p ( y 2 ) p ( y 1 , y 2 ) p ( x ) \begin{gathered} p\left(\boldsymbol{x} \mid \boldsymbol{y}_1, \boldsymbol{y}_2\right)=\eta p\left(\boldsymbol{x} \mid \boldsymbol{y}_1\right) p\left(\boldsymbol{x} \mid \boldsymbol{y}_2\right) \\ \eta=\frac{p\left(\boldsymbol{y}_1\right) p\left(\boldsymbol{y}_2\right)}{p\left(\boldsymbol{y}_1, \boldsymbol{y}_2\right) p(\boldsymbol{x})} \end{gathered} p(x∣y1,y2)=ηp(x∣y1)p(x∣y2)η=p(y1,y2)p(x)p(y1)p(y2)
3 高斯分布
高斯分布是一个理想的分布,在真实世界中,模型往往是非线性非高斯的,为了方便处理,我们经常在使用高斯分布来近似表示真实世界中的PDF的某个点。
3.1 Gaussian PDF
p ( x ∣ μ , σ 2 ) = 1 2 π σ 2 exp ( − 1 2 ( x − μ ) 2 σ 2 ) p\left(x \mid \mu, \sigma^2\right)=\frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left(-\frac{1}{2} \frac{(x-\mu)^2}{\sigma^2}\right) p(x∣μ,σ2)=2πσ21exp(−21σ2(x−μ)2)
p ( x ∣ μ , Σ ) = 1 ( 2 π ) N det Σ exp ( − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) ) p(\boldsymbol{x} \mid \boldsymbol{\mu}, \boldsymbol{\Sigma})=\frac{1}{\sqrt{(2 \pi)^N \operatorname{det} \boldsymbol{\Sigma}}} \exp \left(-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{\mathrm{T}} \boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\right) p(x∣μ,Σ)=(2π)NdetΣ1exp(−21(x−μ)TΣ−1(x−μ))
习惯上,我们也将正态分布(即⾼斯分布)记为:
x ∼ N ( μ , Σ ) \boldsymbol{x} \sim \mathcal{N}(\boldsymbol{\mu}, \boldsymbol{\Sigma}) x∼N(μ,Σ)
标准正态分布(standard normally distributed):
x ∼ N ( 0 , 1 ) \boldsymbol{x} \sim \mathcal{N}(\mathbf{0}, \mathbf{1}) x∼N(0,1)
3.2 高斯推断(贝叶斯推断在高斯分布的一次实现)
p ( x , y ) = p ( x ∣ y ) p ( y ) p ( x ∣ y ) = N ( μ x + Σ x y Σ y y − 1 ( y − μ y ) , Σ x x − Σ x y Σ y y − 1 Σ y x ) p ( y ) = N ( μ y , Σ y y ) \begin{aligned} p(\boldsymbol{x}, \boldsymbol{y}) & =p(\boldsymbol{x} \mid \boldsymbol{y}) p(\boldsymbol{y}) \\ p(\boldsymbol{x} \mid \boldsymbol{y}) & =\mathcal{N}\left(\boldsymbol{\mu}_x+\boldsymbol{\Sigma}_{x y} \boldsymbol{\Sigma}_{y y}^{-1}\left(\boldsymbol{y}-\boldsymbol{\mu}_y\right), \boldsymbol{\Sigma}_{x x}-\boldsymbol{\Sigma}_{x y} \boldsymbol{\Sigma}_{y y}^{-1} \boldsymbol{\Sigma}_{y x}\right) \\ p(\boldsymbol{y}) & =\mathcal{N}\left(\boldsymbol{\mu}_y, \boldsymbol{\Sigma}_{y y}\right) \end{aligned} p(x,y)p(x∣y)p(y)=p(x∣y)p(y)=N(μx+ΣxyΣyy−1(y−μy),Σxx−ΣxyΣyy−1Σyx)=N(μy,Σyy)
推导过程使用的shur complement,将联合概率分布带入gaussian PDF展开,只关注二次项部分
p ( x , y ) = N ( [ μ x μ y ] , [ Σ x x Σ x y Σ y x Σ y y ] ) p(\boldsymbol{x}, \boldsymbol{y})=\mathcal{N}\left(\left[\begin{array}{l} \boldsymbol{\mu}_x \\ \boldsymbol{\mu}_y \end{array}\right],\left[\begin{array}{ll} \boldsymbol{\Sigma}_{x x} & \boldsymbol{\Sigma}_{x y} \\ \boldsymbol{\Sigma}_{y x} & \boldsymbol{\Sigma}_{y y} \end{array}\right]\right) p(x,y)=N([μxμy],[ΣxxΣyxΣxyΣyy])
( [ x y ] − [ μ x μ y ] ) T [ Σ x x Σ x y Σ y x Σ y y ] − 1 ( [ x y ] − [ μ x μ y ] ) = ( [ x y ] − [ μ x μ y ] ) T [ 1 0 − Σ y y − 1 Σ y x 1 ] [ ( Σ x x − Σ x y Σ y y − 1 Σ y x ) − 1 0 0 Σ y y − 1 ] × [ 1 − Σ x y Σ y y − 1 0 1 ] ( [ x y ] − [ μ x μ y ] ) = ( x − μ x − Σ x y Σ y y − 1 ( y − μ y ) ) T ( Σ x x − Σ x y Σ y y − 1 Σ y x ) − 1 × ( x − μ x − Σ x y Σ y y − 1 ( y − μ y ) ) + ( y − μ y ) T Σ y y − 1 ( y − μ y ) \begin{aligned} &\left(\left[\begin{array}{l} \boldsymbol{x} \\ \boldsymbol{y} \end{array}\right]-\left[\begin{array}{l} \boldsymbol{\mu}_x \\ \boldsymbol{\mu}_y \end{array}\right]\right)^{\mathrm{T}}\left[\begin{array}{ll} \boldsymbol{\Sigma}_{x x} & \boldsymbol{\Sigma}_{x y} \\ \boldsymbol{\Sigma}_{y x} & \boldsymbol{\Sigma}_{y y} \end{array}\right]^{-1}\left(\left[\begin{array}{l} \boldsymbol{x} \\ \boldsymbol{y} \end{array}\right]-\left[\begin{array}{l} \boldsymbol{\mu}_x \\ \boldsymbol{\mu}_y \end{array}\right]\right) \\ &=\left(\left[\begin{array}{l} \boldsymbol{x} \\ \boldsymbol{y} \end{array}\right]-\left[\begin{array}{l} \boldsymbol{\mu}_x \\ \boldsymbol{\mu}_y \end{array}\right]\right)^{\mathrm{T}} {\left[\begin{array}{cc} \mathbf{1} & \mathbf{0} \\ -\boldsymbol{\Sigma}_{y y}^{-1} \boldsymbol{\Sigma}_{y x} & \mathbf{1} \end{array}\right]\left[\begin{array}{cc} \left(\boldsymbol{\Sigma}_{x x}-\boldsymbol{\Sigma}_{x y} \boldsymbol{\Sigma}_{y y}^{-1} \boldsymbol{\Sigma}_{y x}\right)^{-1} & \mathbf{0} \\ \mathbf{0} & \boldsymbol{\Sigma}_{y y}^{-1} \end{array}\right] } \\ & \times\left[\begin{array}{cc} \mathbf{1} & -\boldsymbol{\Sigma}_{x y} \boldsymbol{\Sigma}_{y y}^{-1} \\ \mathbf{0} & \mathbf{1} \end{array}\right]\left(\left[\begin{array}{c} \boldsymbol{x} \\ \boldsymbol{y} \end{array}\right]-\left[\begin{array}{c} \boldsymbol{\mu}_x \\ \boldsymbol{\mu}_y \end{array}\right]\right) \\ &=\left(\boldsymbol{x}-\boldsymbol{\mu}_x-\boldsymbol{\Sigma}_{x y} \boldsymbol{\Sigma}_{y y}^{-1}\left(\boldsymbol{y}-\boldsymbol{\mu}_y\right)\right)^{\mathrm{T}}\left(\boldsymbol{\Sigma}_{x x}-\boldsymbol{\Sigma}_{x y} \boldsymbol{\Sigma}_{y y}^{-1} \boldsymbol{\Sigma}_{y x}\right)^{-1} \\ & \times\left(\boldsymbol{x}-\boldsymbol{\mu}_x-\boldsymbol{\Sigma}_{x y} \boldsymbol{\Sigma}_{y y}^{-1}\left(\boldsymbol{y}-\boldsymbol{\mu}_y\right)\right)+\left(\boldsymbol{y}-\boldsymbol{\mu}_y\right)^{\mathrm{T}} \boldsymbol{\Sigma}_{y y}^{-1}\left(\boldsymbol{y}-\boldsymbol{\mu}_y\right) \end{aligned} ([xy]−[μxμy])T[ΣxxΣyxΣxyΣyy]−1([xy]−[μxμy])=([xy]−[μxμy])T[1−Σyy−1Σyx01][(Σxx−ΣxyΣyy−1Σyx)−100Σyy−1]×[10−ΣxyΣyy−11]([xy]−[μxμy])=(x−μx−ΣxyΣyy−1(y−μy))T(Σxx−ΣxyΣyy−1Σyx)−1×(x−μx−ΣxyΣyy−1(y−μy))+(y−μy)TΣyy−1(y−μy)
3.2.1 高斯推断的理解
从状态的先验分布(P(x))出发,结合观测 值 y means y_{\text{means}} ymeans给出x的最佳估计,这个过程可以缩小x的方差,也就是让x的估计变好了。
3.3 高斯分布的线性变换
计算高斯分布的变换的关键就是计算均值和协方差,直接按照公式去推导即可。
3.4 高斯PDF的归一化积(一般PDF归一化积的高斯实现):用于融合同一变量的复合高斯分布的多次观测
成立的前提是:
K 个⾼斯概率密度函数的归⼀化积(参考 2.1.6 节)仍然是⾼斯概率密度函数
其中融合后的均值方差如下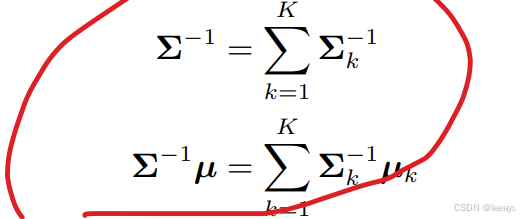
融合后的方差变小,意味着多次融合的估计值更好。
同理我们也可以对高斯分布做线性变换之后的高斯分布做归一化积
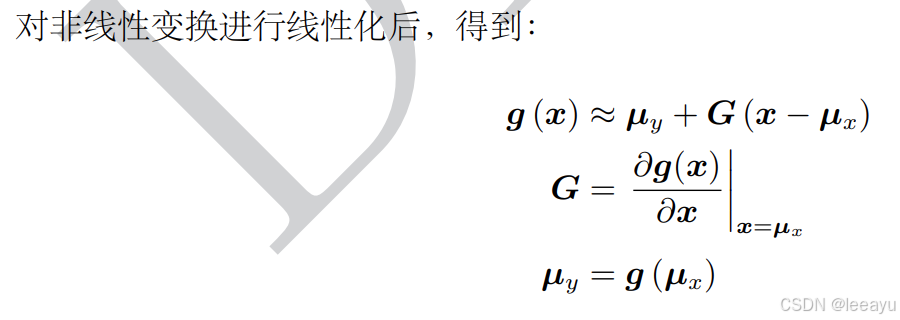
3.5 高斯分布的非线性变换
- 输入:高斯分布P(x), P(y|x)
- 输出:非高斯分布P(y)
- 假设:P(y|x)的噪声是零均值高斯噪声

输出PDF是非高斯分布,这里使用线性化,在输出点用高斯分布近似