阅读量:0
5.4 二叉树的性质和存储结构

5.5 遍历二叉树和线索二叉树
5.5.1 遍历二叉树
先序、中序、后序遍历的递归算法
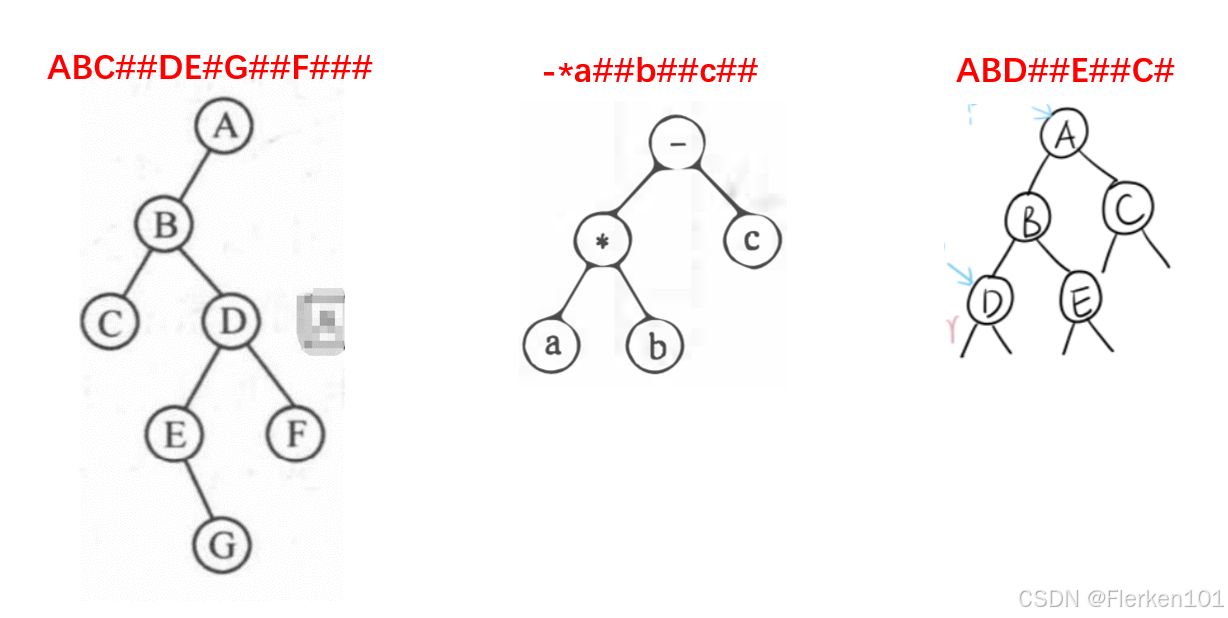
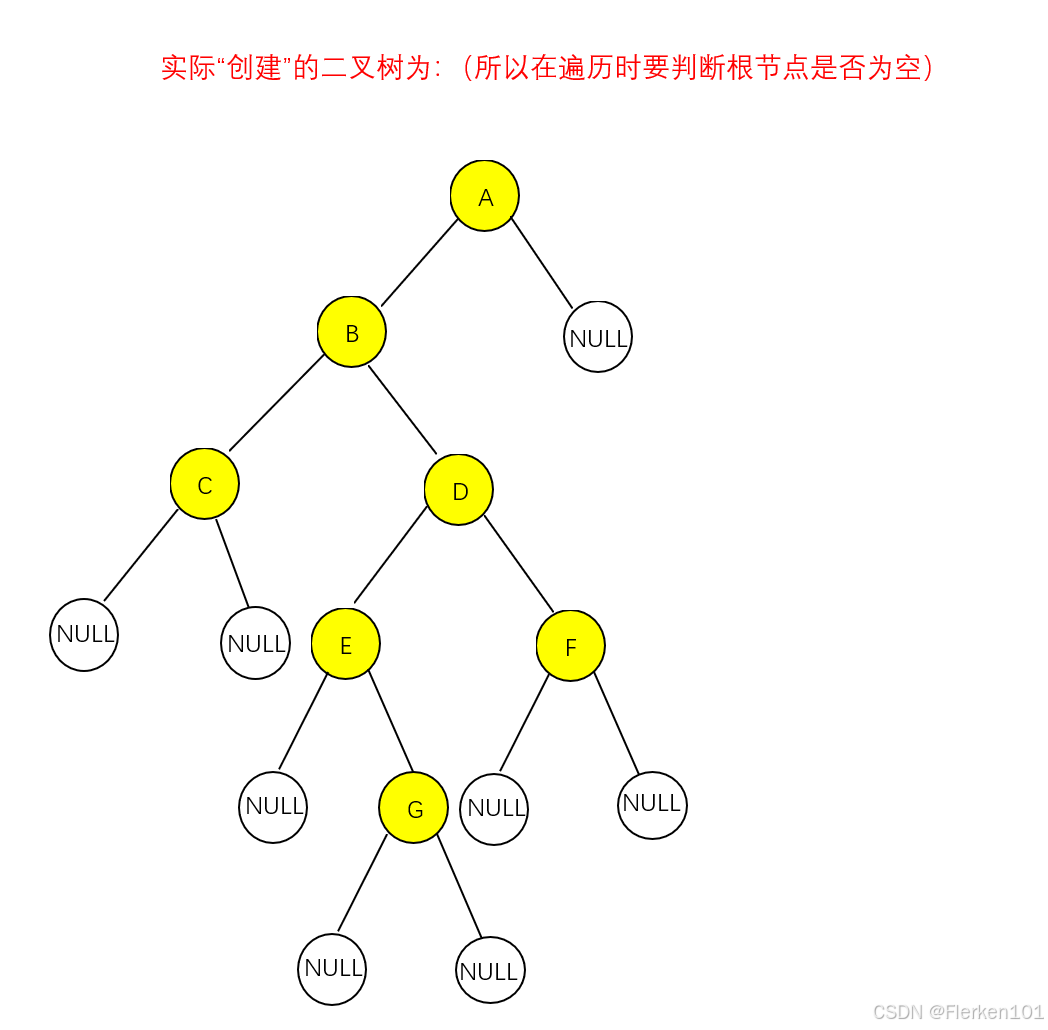
//算法5.1 先序、中序、后序遍历的递归算法 #include <stdio.h> #include <stdlib.h> typedef char TElemType; typedef struct BiTNode { TElemType data; struct BiTNode* lchild; struct BiTNode* rchild; }BiTNode, * BiTree; void InitBiTree(BiTree& T); void CreateBiTree(BiTree& T); void preOrderTraverse(BiTree& T); void InOrderTraverse(BiTree& T); void posOrderTraverse(BiTree& T); //ABC##DE#G##F### int main() { BiTree Tree = NULL; InitBiTree(Tree); printf("请输入要用二叉链表表示的字符序列: "); CreateBiTree(Tree); printf("\n二叉链表的先序序列为: "); preOrderTraverse(Tree); printf("\n二叉链表的中序序列为: "); InOrderTraverse(Tree); printf("\n二叉链表的后序序列为: "); posOrderTraverse(Tree); return 0; } //初始化二叉树 void InitBiTree(BiTree& T) { T = NULL; } //按先序次序输入二叉树中结点的值(一个字符),创建二叉链表表示的二叉树T //由于先序遍历的顺序是“根节点-左子树-右子树”,因此仅有先序可以正确创建二叉树,当根结点为空时,令其整个二叉树为空,而不用管左右子树 void CreateBiTree(BiTree& T) { TElemType ch = '\0'; ch = getchar(); /* getchar从键盘获取且只能获取一个字符。 接收空格和制表符(空格或制表符会被算作一个正常字符读入一次), 不接收回车,遇到回车即认为本次输入结束。 但末尾输入的回车会被留在缓存流中,在下一次被getchar读取到(吃掉回车),并将该回车作为本次输入的结束。 */ //scanf_s(" %c", &ch); //用scanf_s会将整个字符序列写进ch中,无法进行递归创建二叉树 /*scanf_s在输入的末尾遇到空白符(空格符、回车符(\n)和制表符(\t)等) 时,都会认为本次输入结束。 对于参数%d:会忽略缓冲区开头的空白符(空格、回车、制表符等)(无论有几个),只从数字开始读取。 但对输入末尾的非数字字符,包括空白符,则可能进入无限循环程序,使得无法进行下一次输入; 对于参数%c:会直接读取缓冲区的第一个字符(无论这个字符是什么)。 所以一般需要在%c前面加一个空格,利用格式化的输入方式,使得遇到空格的scanf_s认为本次输入已结束, 直接等待下一次输入,而放弃缓冲区内的所有字符,来跳过上一次输入末尾的换行符。 */ if (ch == '#') { T = NULL; } else { T = (BiTree)malloc(sizeof(BiTNode)); T->data = ch; CreateBiTree(T->lchild); CreateBiTree(T->rchild); } } //先序遍历二叉树 void preOrderTraverse(BiTree& T) { if (T) //只有当T不为空时才访问它的成员 { printf(" %c", T->data); preOrderTraverse(T->lchild); preOrderTraverse(T->rchild); } } //中序遍历二叉树 void InOrderTraverse(BiTree& T) { if (T) { InOrderTraverse(T->lchild); printf(" %c", T->data); InOrderTraverse(T->rchild); } } //后序遍历二叉树 void posOrderTraverse(BiTree& T) { if (T) { posOrderTraverse(T->lchild); posOrderTraverse(T->rchild); printf(" %c", T->data); } } 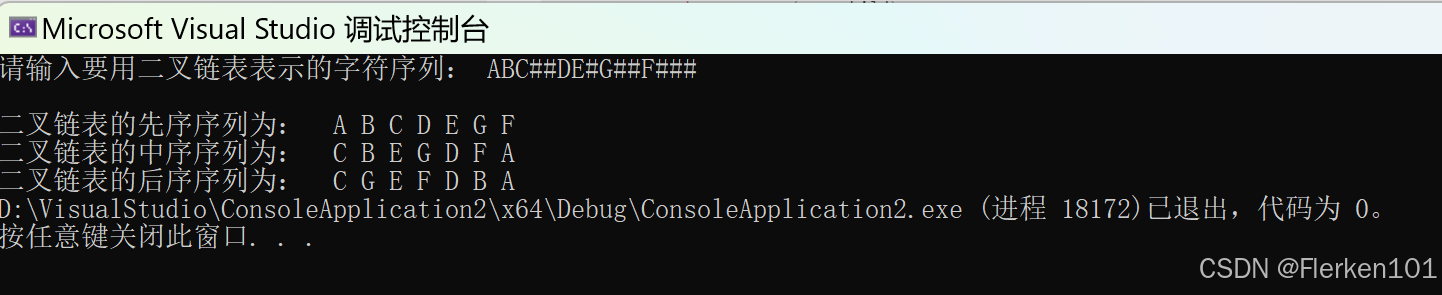
先序、中序、后序遍历的非递归算法
//先序、中序、后序遍历二叉树的非递归算法 #include <stdio.h> #include <stdlib.h> typedef char TElemType; typedef struct BiTNode { TElemType data; struct BiTNode* lchild; struct BiTNode* rchild; }BiTNode, * BiTree; //链栈的数据结构 typedef struct StackNode { BiTree TNodeptr; struct StackNode* next; }StackNode, * LinkStack; void InitStack(LinkStack& S); void Push(LinkStack& S, BiTree p); BiTree Pop(LinkStack& S); BiTree GetTop(LinkStack& S); int EmptyStack(LinkStack& S); void InitBiTree(BiTree& T); void CreateBiTree(BiTree& T); void preOrderTraverse(BiTree& T); void InOrderTraverse(BiTree& T); void posOrderTraverse(BiTree& T); /* 按先序次序输入二叉树中结点的值:(输入的结尾一定是两个#号) ABC##DE#G##F### -*a##b##c## ABD##E##C## */ int main() { BiTree Tree = NULL; InitBiTree(Tree); char choice = '\0'; while (1) { printf("请输入要用二叉链表表示的字符先序序列: "); CreateBiTree(Tree); printf("\n二叉链表的先序序列为: "); preOrderTraverse(Tree); printf("\n二叉链表的中序序列为: "); InOrderTraverse(Tree); printf("\n二叉链表的后序序列为: "); posOrderTraverse(Tree); printf("\n是否继续?(y/n):"); scanf_s(" %c", &choice); getchar(); if (choice != 'y' && choice != 'Y') { break; } printf("\n\n"); } return 0; } //初始化栈 void InitStack(LinkStack& S) { S = NULL; } //元素进栈 void Push(LinkStack& S, BiTree p) { struct StackNode* r = NULL; r = (struct StackNode*)malloc(sizeof(struct StackNode)); if (!r) { printf("创建新结点时,内存分配失败。"); return; } r->TNodeptr = p; r->next = S; S = r; } //栈顶元素出栈 BiTree Pop(LinkStack& S) { if (!S) { printf("弹出栈顶元素时,栈不存在。"); return NULL; } struct StackNode* r = S; BiTree a = S->TNodeptr; S = S->next; free(r); return a; } //获取栈顶元素 BiTree GetTop(LinkStack& S) { if (!S) { printf("获取栈顶元素时,栈不存在。"); return NULL; } return S->TNodeptr; } //判断栈是否为空 int EmptyStack(LinkStack& S) { if (!S) { return 1; } else { return 0; } } //初始化二叉树 void InitBiTree(BiTree& T) { T = NULL; } //按先序次序输入二叉树中结点的值(一个字符),创建二叉链表表示的二叉树T void CreateBiTree(BiTree& T) { TElemType ch = '\0'; ch = getchar(); if (ch == '#') { T = NULL; } else { T = (BiTree)malloc(sizeof(BiTNode)); T->data = ch; CreateBiTree(T->lchild); CreateBiTree(T->rchild); } } //先序遍历二叉树的非递归算法 void preOrderTraverse(BiTree& T) { LinkStack S = NULL; InitStack(S); BiTree p = T; //初始化指向根结点的p为二叉树的根结点T while (p || !EmptyStack(S)) { if (p) { printf("%c", p->data); Push(S, p); p = p->lchild; } else { p = Pop(S); p = p->rchild; } } } //中序遍历二叉树的非递归算法 void InOrderTraverse(BiTree& T) { LinkStack S = NULL; InitStack(S); BiTree p = T; //初始化指向根结点的p为二叉树的根结点T BiTree q = (BiTree)malloc(sizeof(BiTNode)); //可以不设置q,程序里的q直接改为p if (!q) { printf("非递归算法中序遍历二叉树时,用来存放栈顶弹出的指针元素的q内存分配失败。"); return; } while (p || !EmptyStack(S)) { if (p) { Push(S, p); p = p->lchild; } else { q = Pop(S); printf("%c", q->data); p = q->rchild; } } } //后序遍历二叉树的非递归算法 void posOrderTraverse(BiTree& T) { LinkStack S = NULL; InitStack(S); BiTree p = T; BiTree r = NULL;// r标记最近访问过的结点 while (p != NULL || !EmptyStack(S)) { if (p != NULL) { Push(S, p); // 一直向左走,左孩子入栈 p = p->lchild; } else //①只有左孩子为空时(即无法进入第一层if),才会进入else语句,利用栈进行右子树及根结点本身的判断与访问,符合后序遍历的规定 { p = GetTop(S); //获取s的栈顶元素赋值给p,GetTop(s,p)意思就是判断栈顶元素的情况 if (p->rchild && p->rchild != r) //②若右孩子存在且未被访问,则先进行右孩子的后序遍历,再进行根结点本身的访问,符合后序遍历的规定 { p = p->rchild; // 就让右孩子 Push(S, p); //入栈 p = p->lchild; // 让右孩子向左 //上面三句意思就是右孩子的左孩子非空的话就重新进入while循环,入栈,并一直向左走,非空的话就一直入栈 } else //③左子树和右子树都后序遍历完了,最后进行根结点本身的访问。 { p = Pop(S); // 右孩子为空或未被访问过,就出栈 printf("%c", p->data); /* 根结点p的data值已输出,根据后序遍历的过程,以结点p为根结点的二叉树的后续遍历已经完成。 ④接下来应该进行以根结点p为子树的二叉树(假设根结点是x)的后序遍历(所以此步将p置空,进而可以进入第一层else,获取根结点x的信息): 当p是x的左子树根结点时,则应该进行x的右子树(假设根结点是y)的遍历(对应上面第二层if判断); 当p是x的右子树根结点时,则应该进行x的输出。(在上面第二层if判断中,x的右子树即p已经被访问过,所以还会进入该else语句中,弹出x结点) 若p不是子树的根结点,那么就是整个二叉树的根结点(有且仅有这一种情况),说明整个二叉树后序遍历完成了。 */ r = p; // r标记最近访问结点 p = NULL; // p置空 } } } } 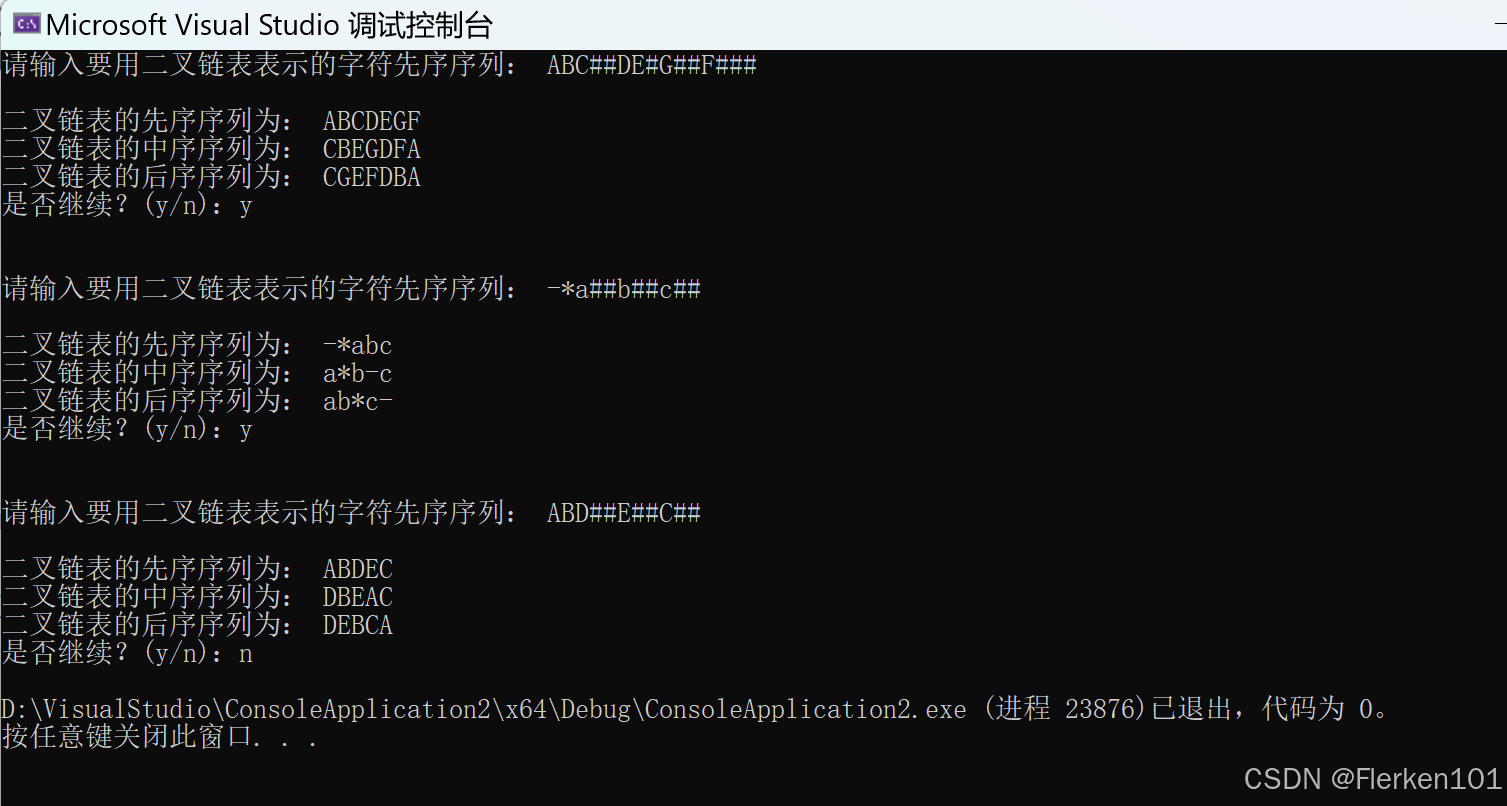
//按先序次序输入二叉树中结点的值:(输入的结尾一定是两个#号): //ABD##E##C## //后序遍历二叉树的非递归算法 void posOrderTraverse(BiTree& T) { LinkStack S = NULL; InitStack(S); BiTree p = T; BiTree r = NULL;// r标记最近访问过的结点 while (p != NULL || !EmptyStack(S)) { if (p != NULL) { printf("\n第一层if中:p = %c\n", p->data); Push(S, p); // 一直向左走,左孩子入栈 p = p->lchild; if (p) { printf("第一层if中:p = %c\n", p->data); } else { printf("第一层if中:p = %c\n", '#'); } } else //①只有左孩子为空时(即无法进入第一层if),才会进入else语句,利用栈进行右子树及根结点本身的判断与访问,符合后序遍历的规定 { p = GetTop(S); //获取s的栈顶元素赋值给p,GetTop(s,p)意思就是判断栈顶元素的情况 printf("第一层else中:p = %c\n", p->data); if (p->rchild && p->rchild != r) //②若右孩子存在且未被访问,则先进行右孩子的后序遍历,再进行根结点本身的访问,符合后序遍历的规定 { printf("第二层if中:p->rchild = %c\n", p->rchild->data); p = p->rchild; // 就让右孩子 Push(S, p); //入栈 p = p->lchild; // 让右孩子向左 //上面三句意思就是右孩子的左孩子非空的话就重新进入while循环,入栈,并一直向左走,非空的话就一直入栈 if (p) { printf("第二层if中:p = %c\n", p->data); } else { printf("第二层if中:p = %c\n", '#'); } } else //③左子树和右子树都后序遍历完了,最后进行根结点本身的访问。 { p = Pop(S); // 右孩子为空或未被访问过,就出栈 printf("输出的p为 : %c\n", p->data); /* 根结点p的data值已输出,根据后序遍历的过程,以结点p为根结点的二叉树的后续遍历已经完成。 ④接下来应该进行以根结点p为子树的二叉树(假设根结点是x)的后序遍历(所以此步将p置空,进而可以进入第一层else,获取根结点x的信息): 当p是x的左子树根结点时,则应该进行x的右子树(假设根结点是y)的遍历(对应上面第二层if判断); 当p是x的右子树根结点时,则应该进行x的输出。(在上面第二层if判断中,x的右子树即p已经被访问过,所以还会进入该else语句中,弹出x结点) 若p不是子树的根结点,那么就是整个二叉树的根结点(有且仅有这一种情况),说明整个二叉树后序遍历完成了。 */ r = p; // r标记最近访问结点 printf("第二层else中:r = %c\n", r->data); p = NULL; // p置空 } } } } 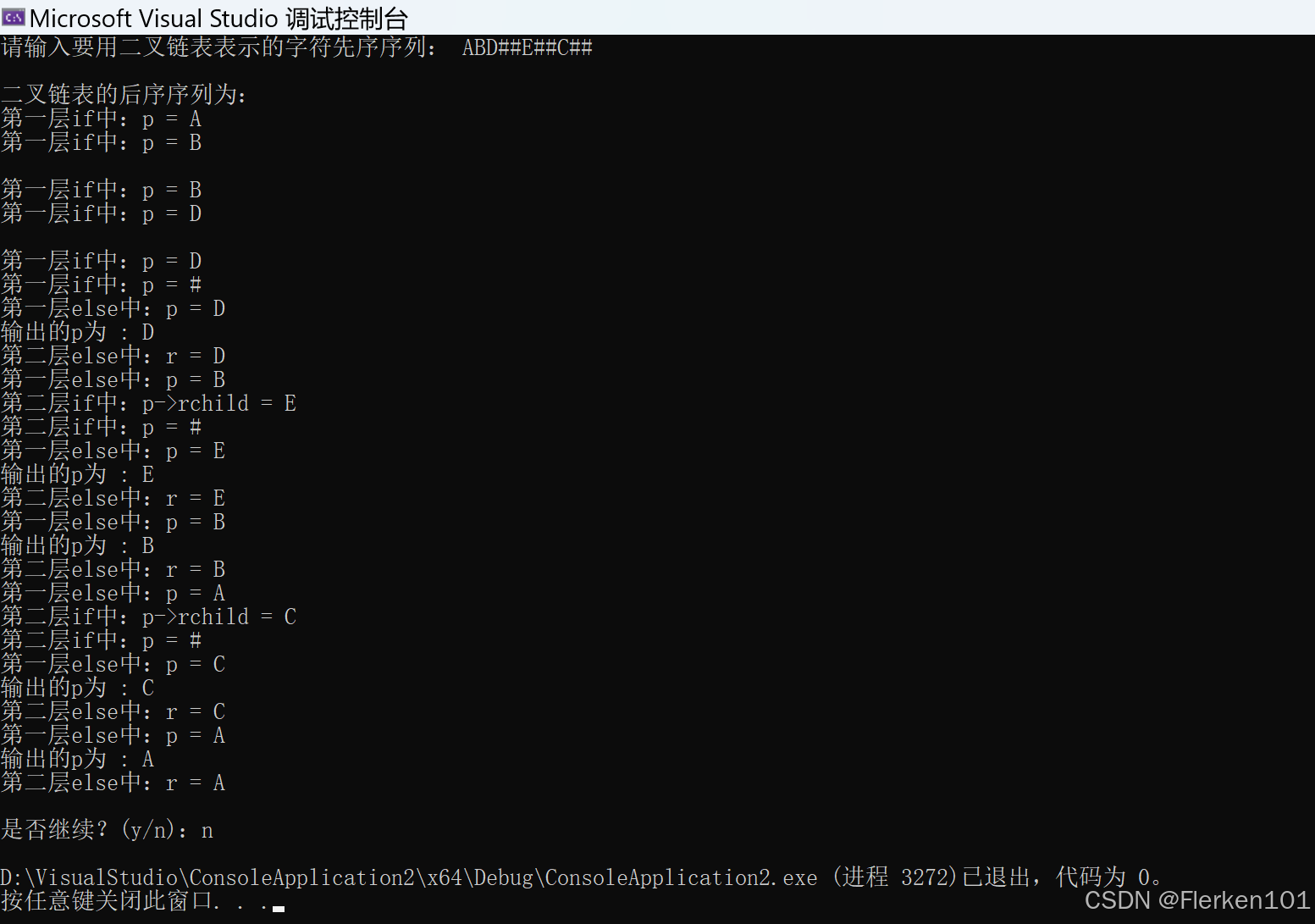
层次遍历的非递归算法
//层次遍历的非递归算法 #include <stdio.h> #include <stdlib.h> typedef char TElemType; //二叉链表 typedef struct BiTNode { TElemType data; struct BiTNode* lchild; struct BiTNode* rchild; }BiTNode,*BiTree; //链队 typedef struct QueueNode { BiTree TNodeptr; struct QueueNode* next; }QueueNode, * QNodeptr; typedef struct { QNodeptr front; QNodeptr rear; }LinkQueue; void InitQueue(LinkQueue& Q); void EnQueue(LinkQueue& Q, BiTree p); BiTree DeQueue(LinkQueue& Q); int EmptyQueue(LinkQueue& Q); void InitBiTree(BiTree& T); void CreateBiTree(BiTree& T); void LevelOrderTraverse(BiTree& T); int main() { BiTree Tree = NULL; InitBiTree(Tree); char choice = '\0'; while (1) { printf("请输入要用二叉链表表示的字符先序序列: "); CreateBiTree(Tree); printf("二叉链表的层次遍历序列为: "); LevelOrderTraverse(Tree); printf("\n是否继续?(y/n):"); scanf_s(" %c", &choice); getchar(); if (choice != 'y' && choice != 'Y') { break; } printf("\n\n"); } return 0; } //初始化链队(有头结点,需要分配内存) void InitQueue(LinkQueue& Q) { Q.front = (QNodeptr)malloc(sizeof(QueueNode)); if (!Q.front) { printf("初始化链队时,内存分配失败。\n"); return; } Q.rear = Q.front; Q.front->next = NULL; } //进队 void EnQueue(LinkQueue& Q, BiTree p) { QNodeptr r = (QNodeptr)malloc(sizeof(QueueNode)); if (!r) { printf("元素进队时,新结点内存分配失败。\n"); return; } r->TNodeptr = p; r->next = NULL; Q.rear->next = r; Q.rear = r; } //出队 BiTree DeQueue(LinkQueue& Q) { if (Q.front == Q.rear) { printf("队头元素出队时,链队为空。\n"); return NULL; } QNodeptr r = Q.front->next; BiTree e = r->TNodeptr; Q.front->next = r->next; if (Q.rear == r) { Q.rear = Q.front; } free(r); return e; } //判空 int EmptyQueue(LinkQueue& Q) { if (Q.front == Q.rear) { return 1; } else { return 0; } } //初始化二叉树 void InitBiTree(BiTree& T) { T = NULL; } //按先序次序输入二叉树中结点的值(一个字符),创建二叉链表表示的二叉树T void CreateBiTree(BiTree& T) { TElemType ch = '\0'; ch = getchar(); if (ch == '#') { T = NULL; } else { T = (BiTree)malloc(sizeof(BiTNode)); T->data = ch; CreateBiTree(T->lchild); CreateBiTree(T->rchild); } } //层次遍历二叉树 void LevelOrderTraverse(BiTree& T) { LinkQueue Q = { NULL,NULL }; InitQueue(Q); BiTree p = T; if (p) { EnQueue(Q,p); while (!EmptyQueue(Q)) { p = DeQueue(Q); printf("%c", p->data); if (p->lchild) { EnQueue(Q, p->lchild); } if (p->rchild) { EnQueue(Q, p->rchild); } } } } 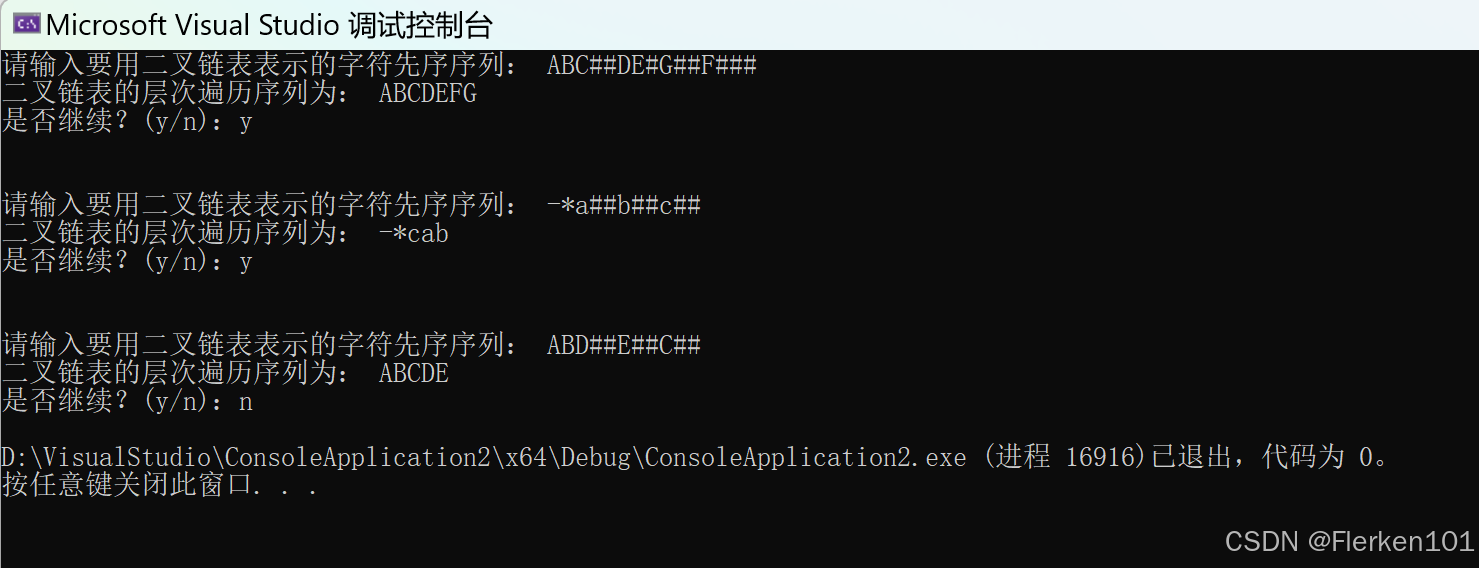
复制二叉树、计算二叉树深度、统计二叉树中结点个数的递归算法
//复制二叉树、计算二叉树深度、统计二叉树中结点个数的递归算法 #include <stdio.h> #include <stdlib.h> typedef char TElemType; typedef struct BiTNode { TElemType data; struct BiTNode* lchild; struct BiTNode* rchild; }BiTNode, * BiTree; void InitBiTree(BiTree& T); void CreateBiTree(BiTree& T); void preOrderTraverse(BiTree& T); void InOrderTraverse(BiTree& T); void posOrderTraverse(BiTree& T); BiTree Copy(BiTree& T); int Depth(BiTree& T); int NodeCount(BiTree T); /* 按先序次序输入二叉树中结点的值:(输入的结尾一定是两个#号) ABC##DE#G##F### -*a##b##c## ABD##E##C## */ int main() { BiTree Tree = NULL; BiTree NewTree = NULL; InitBiTree(Tree); printf("请输入要用二叉链表表示的字符序列: "); CreateBiTree(Tree); printf("\n二叉链表的先序序列为: "); preOrderTraverse(Tree); printf("\n二叉链表的中序序列为: "); InOrderTraverse(Tree); printf("\n二叉链表的后序序列为: "); posOrderTraverse(Tree); printf("\n该二叉链表的深度为:%d", Depth(Tree)); printf("\n该二叉链表的结点个数为:%d", NodeCount(Tree)); NewTree = Copy(Tree); printf("\n\n复制该二叉链表后得到新序列的先序序列为: "); preOrderTraverse(NewTree); printf("\n复制该二叉链表后得到新序列的中序序列为: "); InOrderTraverse(NewTree); printf("\n复制该二叉链表后得到新序列的后序序列为: "); posOrderTraverse(NewTree); printf("\n新序列的深度为:%d", Depth(NewTree)); printf("\n新序列的结点个数为:%d", NodeCount(NewTree)); return 0; } //初始化二叉树 void InitBiTree(BiTree& T) { T = NULL; } //按先序次序输入二叉树中结点的值(一个字符),创建二叉链表表示的二叉树T void CreateBiTree(BiTree& T) { TElemType ch = '\0'; ch = getchar(); if (ch == '#') { T = NULL; } else { T = (BiTree)malloc(sizeof(BiTNode)); T->data = ch; CreateBiTree(T->lchild); CreateBiTree(T->rchild); } } //先序遍历二叉树 void preOrderTraverse(BiTree& T) { if (T) //只有当T不为空时才访问它的成员 { printf(" %c", T->data); preOrderTraverse(T->lchild); preOrderTraverse(T->rchild); } } //中序遍历二叉树 void InOrderTraverse(BiTree& T) { if (T) { InOrderTraverse(T->lchild); printf(" %c", T->data); InOrderTraverse(T->rchild); } } //后序遍历二叉树 void posOrderTraverse(BiTree& T) { if (T) { posOrderTraverse(T->lchild); posOrderTraverse(T->rchild); printf(" %c", T->data); } } //算法5.4 复制二叉树的递归算法 BiTree Copy(BiTree& T) { BiTree NewT = NULL; if (T == NULL) { NewT = NULL; } else { NewT = (BiTree)malloc(sizeof(BiTNode)); NewT->data = T->data; NewT->lchild = Copy(T->lchild); NewT->rchild = Copy(T->rchild); } return NewT; } //算法5.5 计算二叉树深度的递归算法 int Depth(BiTree &T) { if (T == NULL) { return 0; } else { int m = Depth(T->lchild); int n = Depth(T->rchild); //不能从一开始就定义m、n两个变量。否则不管初始化为多少,输出的深度总比实际值小1 if (m > n) { return m + 1; } else { return n + 1; } } } //算法5.6 统计二叉树中结点个数的递归算法 int NodeCount(BiTree T) { if (T == NULL) { return 0; } else { return NodeCount(T->lchild) + NodeCount(T->rchild) + 1; } } 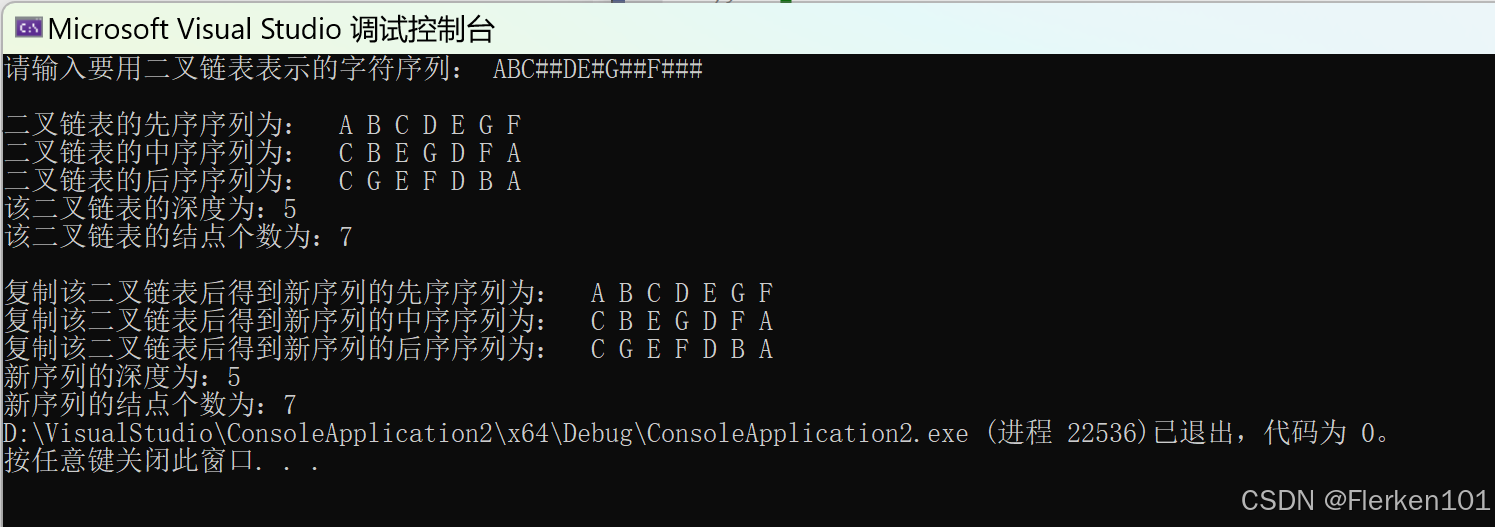
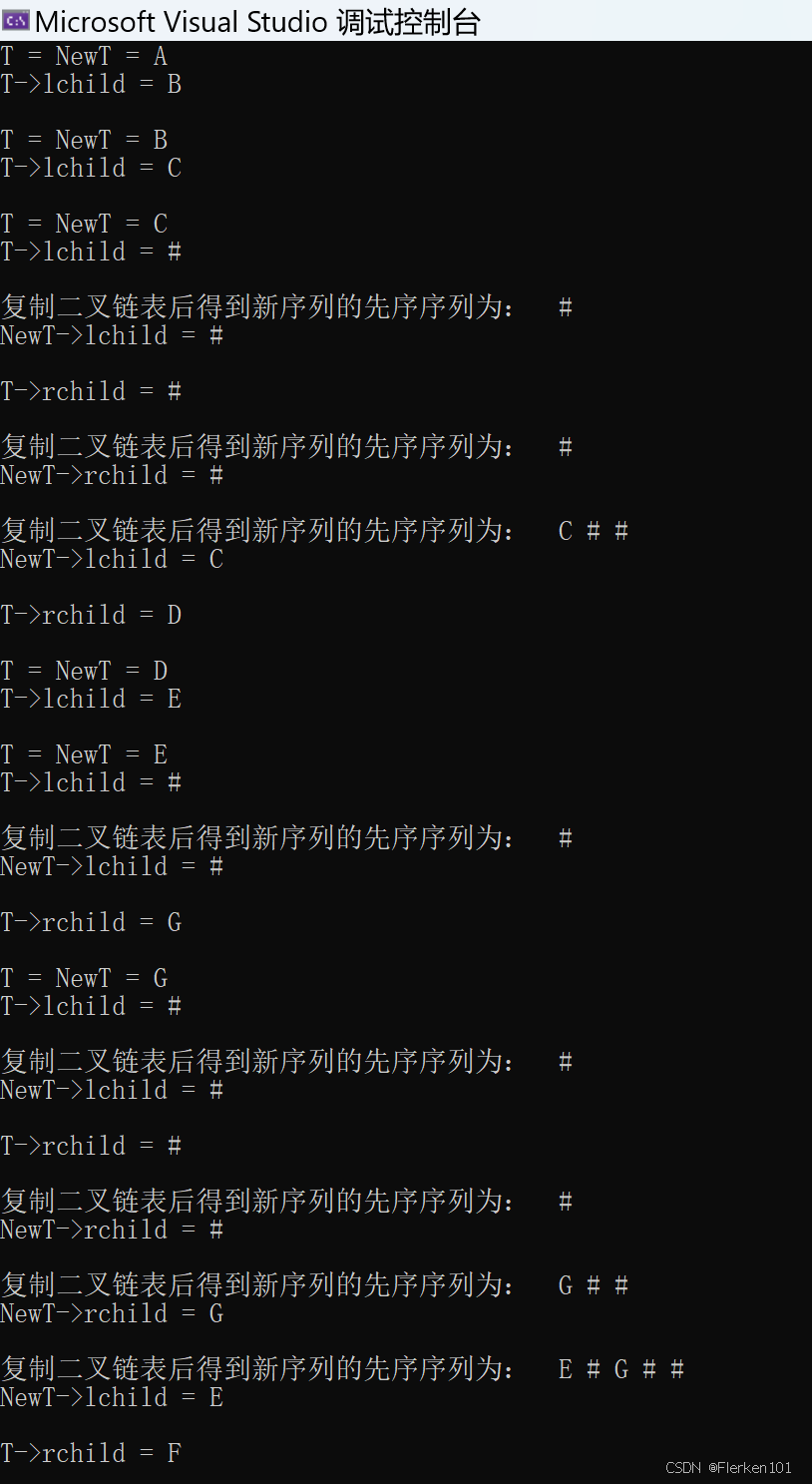
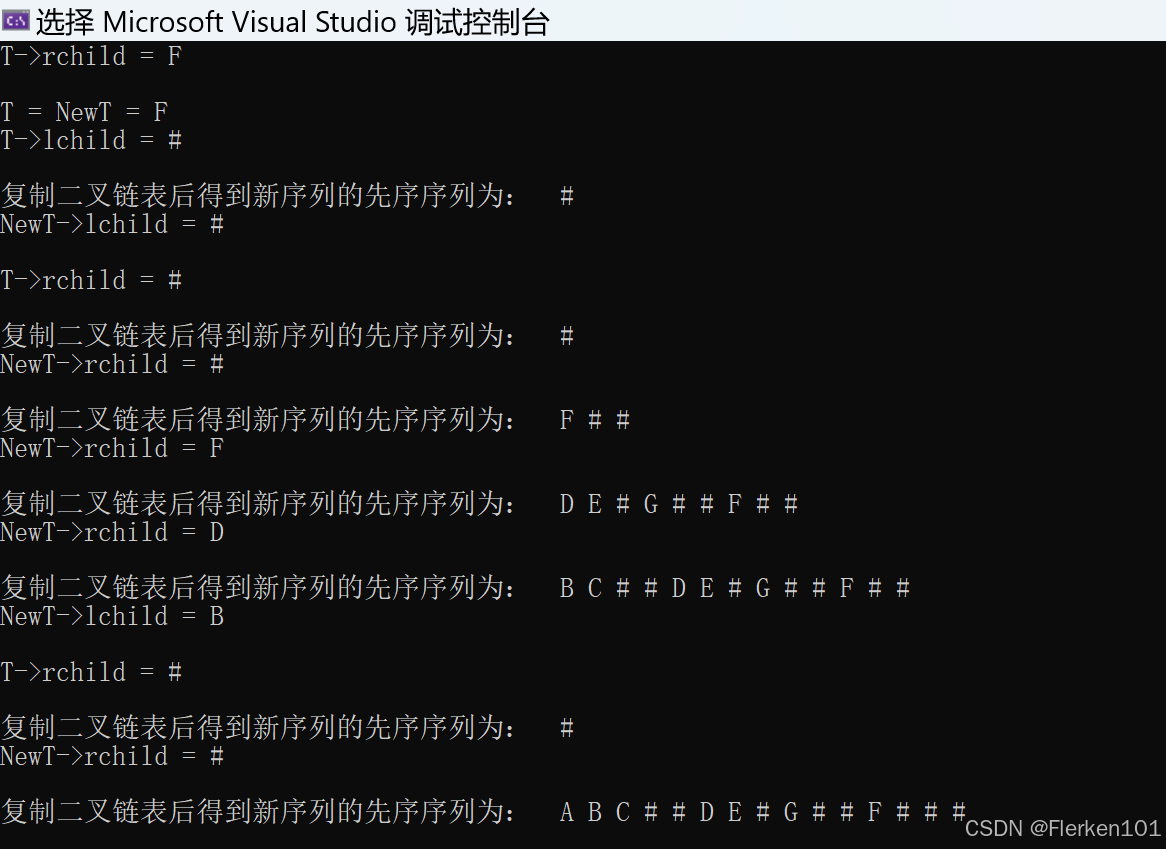
//算法5.4 复制二叉树的递归算法 BiTree Copy(BiTree& T) { BiTree NewT = NULL; if (T == NULL) { NewT = NULL; } else { NewT = (BiTree)malloc(sizeof(BiTNode)); NewT->data = T->data; printf("\nT = NewT = %c\n", NewT->data); if (T->lchild) { printf("T->lchild = %c\n", T->lchild->data); } else { printf("T->lchild = %c\n", '#'); } NewT->lchild = Copy(T->lchild); if (NewT->lchild) { printf("\nNewT->lchild = %c\n", NewT->lchild->data); } else { printf("\nNewT->lchild = %c\n", '#'); } if (T->rchild) { printf("\nT->rchild = %c\n", T->rchild->data); } else { printf("\nT->rchild = %c\n", '#'); } NewT->rchild = Copy(T->rchild); if (NewT->rchild) { printf("\nNewT->rchild = %c\n", NewT->rchild->data); } else { printf("\nNewT->rchild = %c\n", '#'); } } printf("\n复制二叉链表后得到新序列的先序序列为: "); preOrderTraverse(NewT); return NewT; } //先序遍历二叉树 void preOrderTraverse(BiTree& T) { if (T) //只有当T不为空时才访问它的成员 { printf(" %c", T->data); preOrderTraverse(T->lchild); preOrderTraverse(T->rchild); } else { printf(" %c", '#'); } } 
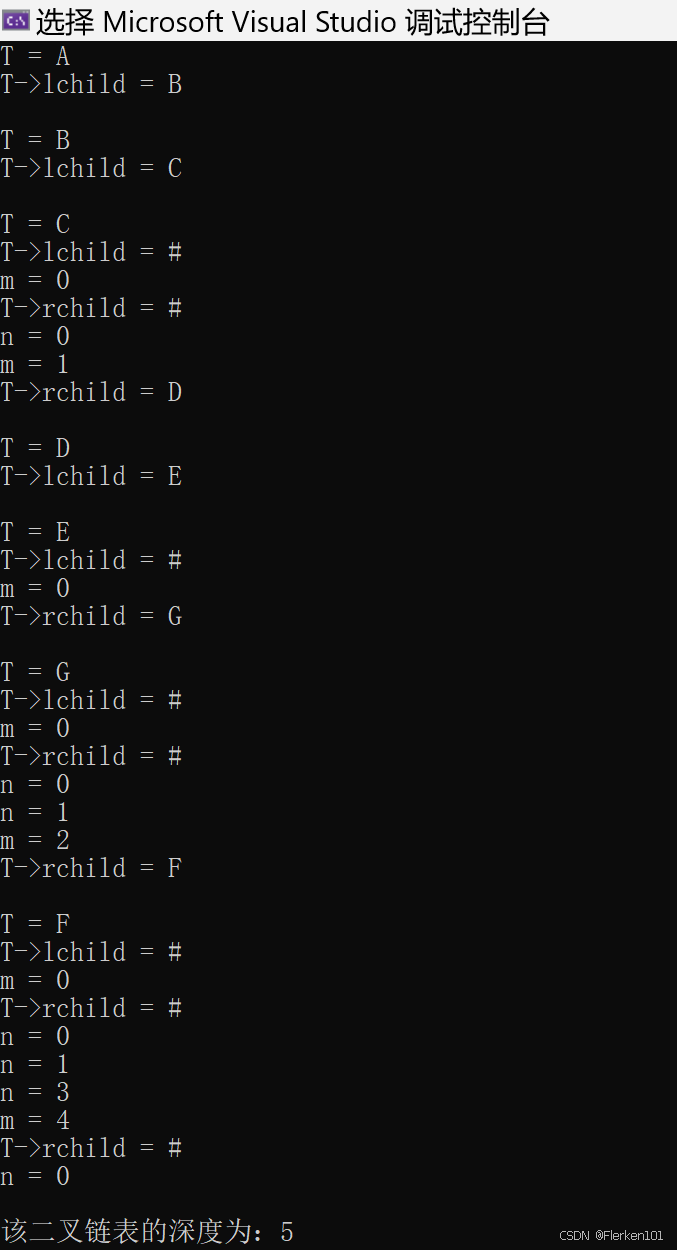
//算法5.5 计算二叉树深度的递归算法 int Depth(BiTree &T) { if (T == NULL) { return 0; } else { printf("\nT = %c\n", T->data); if (T->lchild) { printf("T->lchild = %c\n", T->lchild->data); } else { printf("T->lchild = %c\n", '#'); } int m = Depth(T->lchild); printf("m = %d\n", m); if (T->rchild) { printf("T->rchild = %c\n", T->rchild->data); } else { printf("T->rchild = %c\n", '#'); } int n = Depth(T->rchild); printf("n = %d\n", n); //不能从一开始就定义m、n两个变量。否则不管初始化为多少,输出的深度总比实际值小1 if (m > n) { return m + 1; } else { return n + 1; } } } 
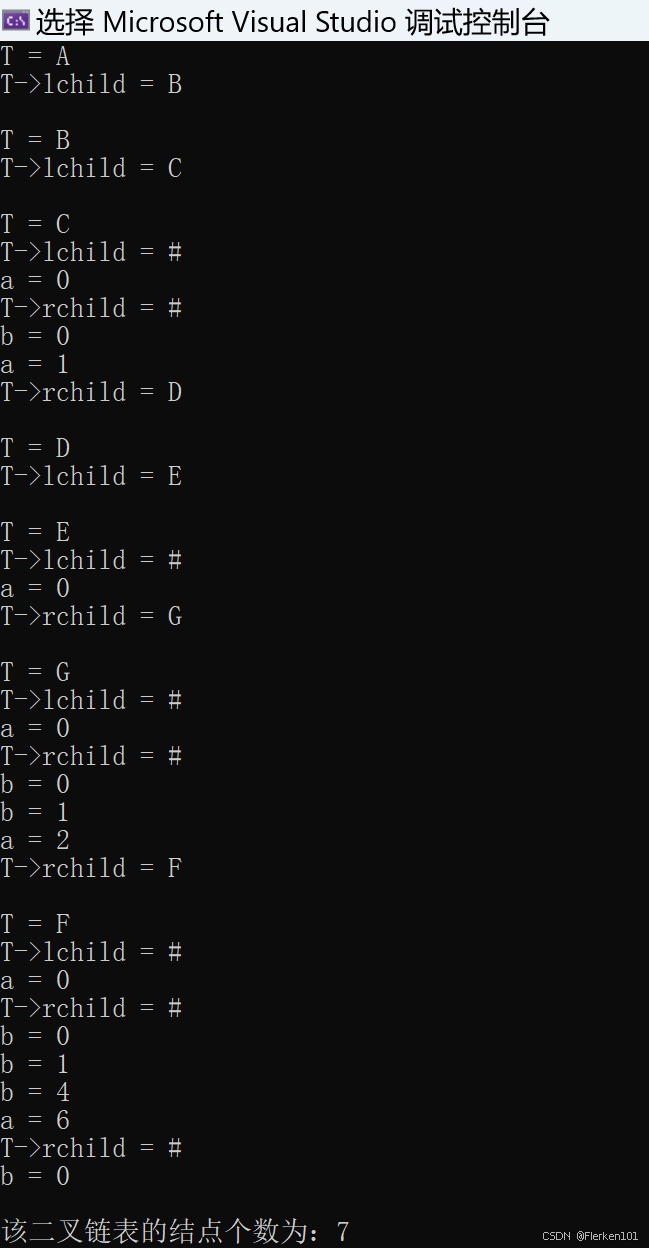
//算法5.6 统计二叉树中结点个数的递归算法 int NodeCount(BiTree T) { if (T == NULL) { return 0; } else { printf("\nT = %c\n", T->data); if (T->lchild) { printf("T->lchild = %c\n", T->lchild->data); } else { printf("T->lchild = %c\n", '#'); } int a = NodeCount(T->lchild); printf("a = %d\n", a); if (T->rchild) { printf("T->rchild = %c\n", T->rchild->data); } else { printf("T->rchild = %c\n", '#'); } int b = NodeCount(T->rchild); printf("b = %d\n", b); return a + b + 1; } } 
复制二叉树、计算二叉树深度、统计二叉树中结点个数的非递归算法
统计二叉树中叶结点(度为 0) 的个数、度为1的结点个数、度为2的结点个数、计算二叉树第k层的结点个数、查找二叉树中的目标值的递归算法
数据结构 统计二叉树中度为0,1和2的结点个数—— 1900_
二叉树的基本操作(如何计算二叉树的结点个数,二叉树的高度) —— 初阶牛
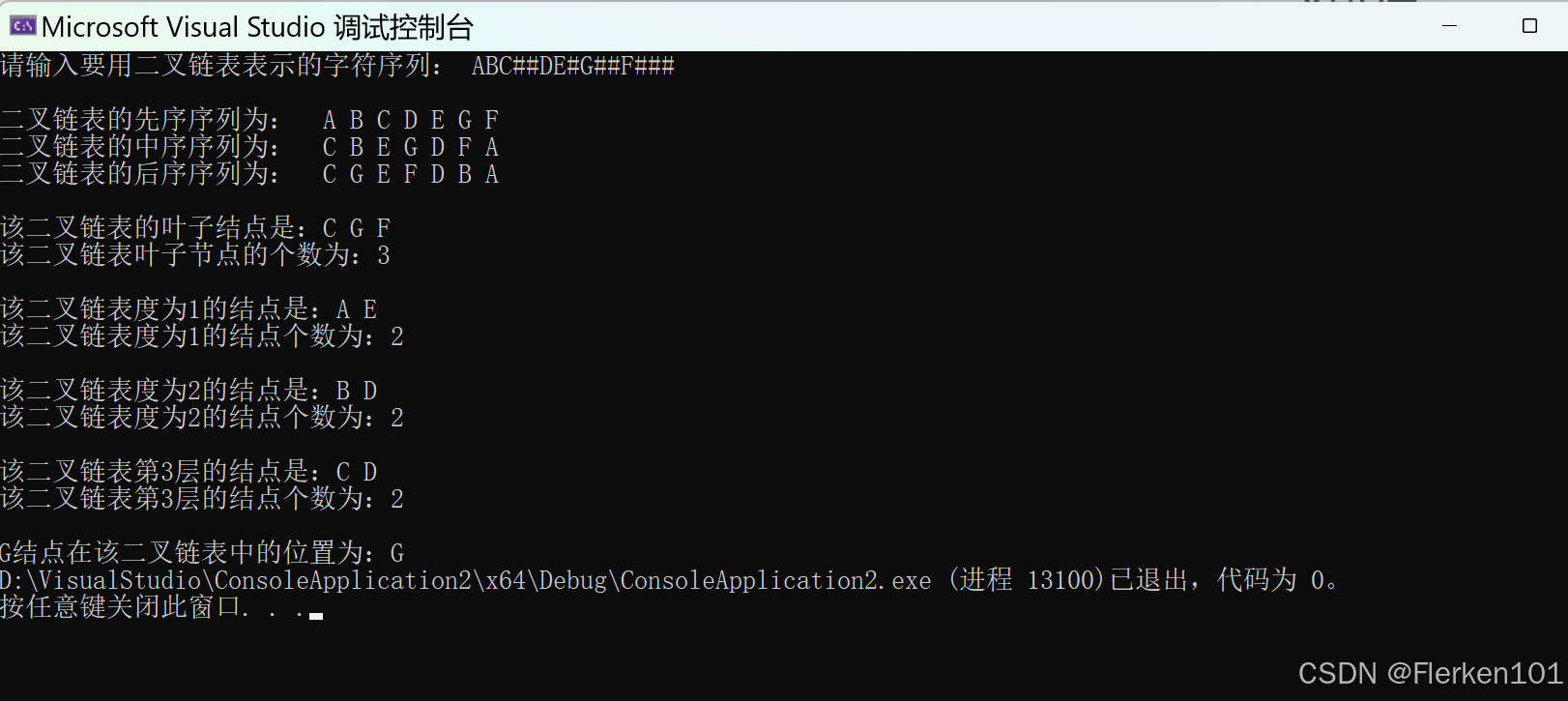
//统计二叉树中叶结点(度为 0) 的个数,度为1的结点个数和度为2的结点个数的递归算法 //计算二叉树第k层的结点个数的递归算法 //查找二叉树中的目标值的递归算法 #include <stdio.h> #include <stdlib.h> typedef char TElemType; typedef struct BiTNode { TElemType data; struct BiTNode* lchild; struct BiTNode* rchild; }BiTNode, * BiTree; void InitBiTree(BiTree& T); void CreateBiTree(BiTree& T); void preOrderTraverse(BiTree& T); void InOrderTraverse(BiTree& T); void posOrderTraverse(BiTree& T); int LeafNodeCount(BiTree T); int NodeCount_1(BiTree T); int NodeCount_2(BiTree T); int NodeCount_kLevel(BiTree T, int k); //计算二叉树第k层的结点个数的递归算法 BiTree FindNode(BiTree T, TElemType e); //查找二叉树中的目标值的递归算法 /* 按先序次序输入二叉树中结点的值:(输入的结尾一定是两个#号) ABC##DE#G##F### -*a##b##c## ABD##E##C## */ int main() { BiTree Tree = NULL; InitBiTree(Tree); printf("请输入要用二叉链表表示的字符序列: "); CreateBiTree(Tree); printf("\n二叉链表的先序序列为: "); preOrderTraverse(Tree); printf("\n二叉链表的中序序列为: "); InOrderTraverse(Tree); printf("\n二叉链表的后序序列为: "); posOrderTraverse(Tree); printf("\n\n该二叉链表的叶子结点是:"); printf("\n该二叉链表叶子节点的个数为:%d", LeafNodeCount(Tree)); printf("\n\n该二叉链表度为1的结点是:"); printf("\n该二叉链表度为1的结点个数为:%d", NodeCount_1(Tree)); printf("\n\n该二叉链表度为2的结点是:"); printf("\n该二叉链表度为2的结点个数为:%d", NodeCount_2(Tree)); printf("\n\n该二叉链表第%d层的结点是:",3); printf("\n该二叉链表第%d层的结点个数为:%d", 3, NodeCount_kLevel(Tree,3)); printf("\n\n%c结点在该二叉链表中的位置为:%c", 'G', (FindNode(Tree, 'G'))->data); return 0; } //初始化二叉树 void InitBiTree(BiTree& T) { T = NULL; } //按先序次序输入二叉树中结点的值(一个字符),创建二叉链表表示的二叉树T void CreateBiTree(BiTree& T) { TElemType ch = '\0'; ch = getchar(); if (ch == '#') { T = NULL; } else { T = (BiTree)malloc(sizeof(BiTNode)); T->data = ch; CreateBiTree(T->lchild); CreateBiTree(T->rchild); } } //先序遍历二叉树 void preOrderTraverse(BiTree& T) { if (T) //只有当T不为空时才访问它的成员 { printf(" %c", T->data); preOrderTraverse(T->lchild); preOrderTraverse(T->rchild); } } //中序遍历二叉树 void InOrderTraverse(BiTree& T) { if (T) { InOrderTraverse(T->lchild); printf(" %c", T->data); InOrderTraverse(T->rchild); } } //后序遍历二叉树 void posOrderTraverse(BiTree& T) { if (T) { posOrderTraverse(T->lchild); posOrderTraverse(T->rchild); printf(" %c", T->data); } } //统计二叉树中叶结点(度为 0) 的个数的递归算法 int LeafNodeCount(BiTree T) { if (T == NULL) { return 0; } else { if (T->lchild == NULL && T->rchild == NULL) //判断是否是叶子结点 { printf("%c ", T->data); return 1; } else { int left = LeafNodeCount(T->lchild); //统计左子树中叶子结点的个数 int right = LeafNodeCount(T->rchild); //统计右子树中叶子结点的个数 return left + right; } } } //统计二叉树中度为1的结点个数的递归算法 int NodeCount_1(BiTree T) { if (T == NULL) { return 0; } else { //判断结点的度是否为1 if ((T->lchild == NULL && T->rchild != NULL) || (T->lchild != NULL && T->rchild == NULL)) { printf("%c ", T->data); int left = NodeCount_1(T->lchild); //统计根结点T左子树中度为1的结点个数 int right = NodeCount_1(T->rchild); //统计根结点T右子树中度为1的结点个数 return 1 + left + right; //前面加1是因为该根结点T本身是度为1的结点 } else //T的左右子树都不为空或者都为空,T均不是度为1的结点,所以不加1 { int left = NodeCount_1(T->lchild); //统计根结点T左子树中度为1的结点个数 int right = NodeCount_1(T->rchild); //统计根结点T右子树中度为1的结点个数 return left + right; } } } //统计二叉树中度为2的结点个数的递归算法 int NodeCount_2(BiTree T) { if (T == NULL) { return 0; } else { //判断结点的度是否为2 if (T->lchild != NULL && T->rchild != NULL) { printf("%c ", T->data); int left = NodeCount_2(T->lchild); //统计根结点T左子树中度为2的结点个数 int right = NodeCount_2(T->rchild); //统计根结点T右子树中度为2的结点个数 return 1 + left + right; //前面加1是因为该根结点T本身是度为2的结点 } else //T的左右子树有一个为空,或者均为空,T均不是度为2的结点,所以不加1 { int left = NodeCount_2(T->lchild); //统计根结点T左子树中度为2的结点个数 int right = NodeCount_2(T->rchild); //统计根结点T右子树中度为2的结点个数 return left + right; } } } //计算二叉树第k层的结点个数的递归算法【不超过2^(k-1)个】 //当k大于1时,第k层的结点个数 = 第k-1层的左子树结点个数 + 第k-1层的右子树结点个数 int NodeCount_kLevel(BiTree T, int k) { if (T == NULL) { return 0; } else { if (k == 1) { printf("%c ", T->data); return 1; } else { int left = NodeCount_kLevel(T->lchild, k - 1); int right = NodeCount_kLevel(T->rchild, k - 1); return left + right; } } } //查找二叉树中的目标值的递归算法 BiTree FindNode(BiTree T,TElemType e) { if (T == NULL) { return NULL; } else if(T->data == e) //先判断根节点 { return T; } else { //先搜索左子树 BiTree left = FindNode(T->lchild, e); if (left) { return left; //如果左子树找到了就返回左子树找到的结点 } //再搜索右子树 BiTree right = FindNode(T->rchild, e); if (right) { return right; //如果右子树找到了就返回右子树找到的结点 } return NULL; //左右子树都没找到 } }