阅读量:0
思路:因为要求XOR最大值,所以两数XOR的时候两数二进制位要是最多的才行,一个数的二进制位是1的同时,另外一个数对应的二进制位是0,这样不一样的二进制位的数量最多时,两数XOR结果最大!
具体操作是先把a[i]以二进制形式插入到Trie树里面,然后Trie查询a【i】,一条路劲沿着a【i】这个二进制路径往深处搜索,从高位搜索,如果当前a【i】里面某一位是0,那么要找到a【i】这路径的对应的1的旁边的一条路径,如果不存在这路径就往下一层搜索,然后遍历a完了之后只花费了 O ( n ) O(n) O(n)时间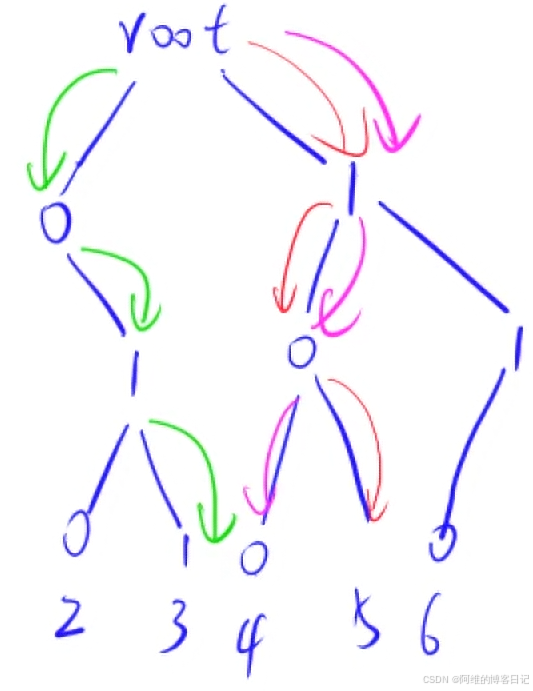
#include<iostream> #define MAX 30000086 #define LEN 100086 using namespace std; int N,a[LEN],son[MAX][2],idx; void insert(int x){ int p=0; for(int i=30;~i;--i){ int u=(x>>i)&1;//2进制的题意,Trie树只有2种状态,0和1 if(!son[p][u]) son[p][u]=++idx; p=son[p][u]; } } int query(int x){ int p=0,res=0; for(int i=30;~i;--i){//~i等价于i>=0,i==-1是为OxFFFFF,取反之后就是0x0000, int u=x>>i&1; if(son[p][!u]){//存在相反2进制位,则把这个数算出来,然后往深一层遍历 res+=1<<i; p=son[p][!u]; } else p=son[p][u];//如果不存在相反2进制位,则往深一层遍历 } return res; } int main(){ cin>>N; for(int i=0;i<N;i++){ cin>>a[i]; insert(a[i]); } int res=0; for(int i=0;i<N;i++){ res=max(res,query(a[i])); } cout<<res<<endl; return 0; } 