算法学习day27

一、寻找重复数(链表中找环)

给定一个包含 n + 1 个整数的数组 nums ，其数字都在 [1, n] 范围内（包括 1 和 n），可知至少存在一个重复的整数。

假设 nums 只有 一个重复的整数 ，返回 这个重复的数 。

题意：

给定大小为n+1的整数数组nums,元素的范围在[1,n]中，必然有一个重复的数字。如何通过找环的思想处理这道题？当我们将数组的值和下标对应在一起的时候，有一个值是对应两个下标的。因此在这里一定会形成环。

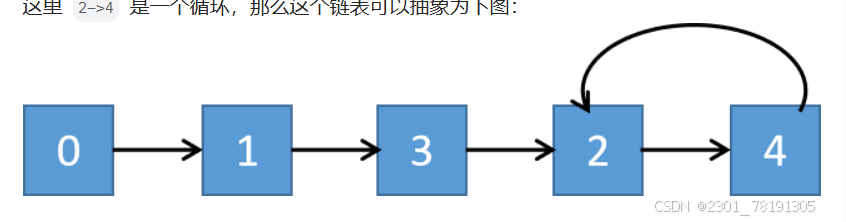
eg：[1,3,4,2,2]。以下标0为起始，nums[i]作为下一个下标。

1.下标为0，下一个下标为nums[0]=1，1不仅为下一个下标，也为当前的值。

2.下标为1，下一个下标为nums[1]=3,

3.下标为3,下一个下标为nums[3]=2;

4.下标为2，下一个下标为nums[2]=4;

5.下标为4，下一个下标为nums[4]=2;

现在有两个位置的下标可以到达2，因此就有环出现了。

思路：

通过之前环形链表II的思路：快慢指针相遇代表有环，然后头结点到入口的距离=相遇点到入口的距离。这样就可以找到入口，也就是重复的数。

代码：

class Solution {     public int findDuplicate(int[] nums) {         int slow=0;         int fast=0;         slow=nums[slow];         fast=nums[nums[fast]];         while(slow!=fast){             slow=nums[slow];             fast=nums[nums[fast]];         }         //slow和fast一定会相遇的 题目中给出来了         int head=0;         while(slow!=head){             head=nums[head];             slow=nums[slow];         }         return head;     } }

二、分段链表(奇偶链表、分割链表)

题意：

就是根据某种要求将链表重新拼接起来。比如说：将所有索引为奇数的节点和索引为偶数的节点分别组合在一起，然后返回重新排序的列表。又或者说,将链表中元素>=k的都放到后面，<k的都放到前面。

思路：做这种题的思路就是，重新建立一个newHead，把另一组的节点都放到newHead后面，然后两段链表连起来就行。

比如说：奇偶链表：如果(下标值+1)%2==0，说明是偶数节点；偶数节点.next=null;然后把偶数节点放到newHead后面。循环完之后，把newHead.next放到cur的后面就行了

代码：

class Solution {     public ListNode oddEvenList(ListNode head) {         ListNode dummyHead=new ListNode();         dummyHead.next=head;         ListNode cur1=dummyHead;         ListNode newHead=new ListNode();         ListNode cur2=newHead;         int index=1;         while(cur1.next!=null){             if(index%2==0){                 ListNode temp=cur1.next;                 cur1.next=cur1.next.next;                 temp.next=null;                 cur2.next=temp;                 cur2=cur2.next;                 index++;             }else{                 cur1=cur1.next;                 index++;             }         }         cur1.next=newHead.next;         return dummyHead.next;     } }

三、相交链表

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。

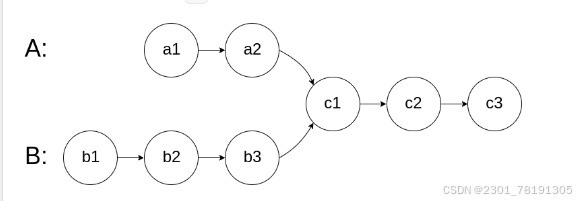
思路：如果两个单链表有相交的节点。那么从0开始到相交节点的距离一定是一样的。

但是问题在于两个链表的起始节点位置不一样。eg：A从位置1出发，B从位置0出发。

那么如何才能让他们走的距离是一样的。假如A到相交节点的距离是:x;B到相交节点的距离是：y。

相交链表的长度是c; x+c+y=y+c=x。这样的距离一定是相等的。

A走到null(x+c)就去headB继续走(y);

B走到null(y+c)就去headA继续走(x); 

直到A和B相等

代码：

public class Solution {     public ListNode getIntersectionNode(ListNode headA, ListNode headB) {         ListNode A=headA,B=headB;         while(A!=B){             A=A==null?headB:A.next;             B=B==null?headA:B.next;         }         return A;     } }

四、供暖器(二分查找)

现在，给出位于一条水平线上的房屋 houses 和供暖器 heaters 的位置，请你找出并返回可以覆盖所有房屋的最小加热半径。

思路：

这道题中的思路就是：遍历每一个房屋houses,找距离它最近的供暖器，然后计算出半径。然后取一个能满足所有房屋都能被供暖的半径。

有三种情况：

1.房屋在最左边，左边没有供暖器了，只有右边有，那么半径等于右边第一个供暖器的位置-房屋的位置

2.房屋在最右边，右边没有供暖器了，只有左边有，那么半径等于左边第一个供暖器的位置-房屋的位置

3.房屋的左右都用供暖器，找距离它最近的供暖器，然后计算半径。难点：如何找到距离该房屋最近的供暖器？找到下标比它大的第一个供暖器，然后找到第一个比他小的供暖器，比较两个就行了

使用二分法找下标比它大的第一个供暖器

代码：

class Solution {     public int findRadius(int[] houses, int[] heaters) {         //先对供暖器的位置进行升序排         Arrays.sort(heaters);         int res=Integer.MIN_VALUE;         int d=0;         for(int i=0;i<houses.length;i++){             //房屋的左边没有供暖器             if(houses[i]<=heaters[0])d=heaters[0]-houses[i];             //房屋的右边没有供暖器             else if(houses[i]>=heaters[heaters.length-1])d=houses[i]-heaters[heaters.length-1];             else{                 int left=0;                 int right=heaters.length-1;                 while(left<right){                     int mid=(left+right)>>1;//右移 取中间值                     if(heaters[mid]<houses[i])left=mid+1;                     else right=mid;                 }                 d=Math.min(heaters[left]-houses[i],houses[i]-heaters[left-1]);             }             res=Math.max(res,d);         }         return res;     } }

五、有效的完全平方数(二分法)

解法一：数学规律

对于一个完全平方数而言，可以写成这样的形式：num=1+3+5+...+(2∗n−1)

class Solution {     public boolean isPerfectSquare(int num) {         int n=1;         while(num>0){             num-=n;             n+=2;         }         return num==0;     } }

解法二：二分法

要从0->n中获取一个数字使得n^2=num,使用二分法是比较合适的。

注意：在判断n^2和num是否相等时，为了防止溢出使用mid和num/mid进行判断；

mid<num/mid;说明目标值在右边区域中,left=mid+1;

mid>num/mid;说明目标值在左边区域中,right=mid;

mid==num/mid:有可能是精度缺失后相等，因此要特别注意(num%mid==0)

class Solution {     public boolean isPerfectSquare(int num) {         if(num==1)return true;         int left=0,right=num;         while(left<right){             int mid=left+(right-left)/2;             if(num/mid>mid)left=mid+1;             else if(num/mid<mid)right=mid;             else{                 if(num%mid!=0)return false;                 return true;             }         }         return false;     } }

六、有序数组中的单一元素

给你一个仅由整数组成的有序数组，其中每个元素都会出现两次，唯有一个数只会出现一次。

请你找出并返回只出现一次的那个数。必须满足 O(log n) 时间复杂度和 O(1) 空间复杂度。

思路：

如何将这道题和二分法联系起来？  根据题意我们可以发现规律：

在没有出现单个元素之前，奇数下标的值一定和它的前一个下标值相等；偶数下标的值一定和它下一个下标的值相等。

如果下标mid满足上面的规律，那么mid之前的数字都满足，更新left=mid+1；

如果下标mid不满足上面的规律，那么mid之后的数字都不满足，更新right=mid;

代码：

class Solution {     public int singleNonDuplicate(int[] nums) {         //奇数下标：如果前面没有单个数字 一定和前一个值相等         //偶数下标：如果前面没有单个数字 一定和后一个值相等         int size=nums.length;         int left=0,right=size-1;         while(left<right){             int mid=left+(right-left)/2;             if(mid%2==0){                 if(mid+1<size&&nums[mid]==nums[mid+1]){                     left=mid+1;                 }else{                     right=mid;                 }             }else{                 if(mid-1>=0&&nums[mid-1]==nums[mid]){                     left=mid+1;                 }else{                     right=mid;                 }             }         }         return nums[left];     } }

七、在排序数组中查找元素的第一个位置和最后一个位置(好题)

解法一：二分查找target后，while循环寻找最左边和最右边

class Solution {     public int[] searchRange(int[] nums, int target) {         int left=0;         int right=nums.length-1;         int[] res=new int[]{-1,-1};         while(left<right){             int mid=left+(right-left)/2;             if(nums[mid]>target)right=mid;             else if(nums[mid]<target)left=mid+1;             else{                 //找到target寻找最左边和最右边                 int start=mid;                 int end=mid;                 while(start>=0&&nums[start]==target)start--;                 while(end<nums.length&&nums[end]==target)end++;                 res[0]=start+1;                 res[1]=end-1;                 break;             }         }         return res;     } }

解法二：

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。如果数组中不存在目标值 target，返回 [-1, -1]。

思路：

以往我们使用二分搜索target的时候，当nums[mid]==target的时候，就返回mid了。此时就找到了数组中哪一个下标的值为target。

但是如果让我们找元素的第一个位置，就需要我们把右边相等的元素都筛除掉。那么应该如何删除？(只有在更新右边区域的时候才能筛除掉右边元素)所以只有当nums[i]>=target的时候，right=mid; (这样mid之后相等的元素就被筛除掉了) else left=mid+1

如果让我们找元素的最后一个位置，就需要我们把左边相等的元素都筛除掉。那么应该如何删除？

 当nums[mid]<=target的时候,left=mid  else right=mid-1;

注意：1.在找元素最后一个位置的时候，如果mid=(left+right)/2 此时如果left+1=right 那么mid一直会是left，会一直陷入循环中，此时就必须把mid=(left+right+1)/2

代码：

class Solution {     public int[] searchRange(int[] nums, int target) {         int[] res = new int[] { -1, -1 };         if (nums.length == 0)             return res;         int left = 0;         int right = nums.length - 1;         // 先找target左边第一个元素         while (left < right) {             int mid = left + (right - left) / 2;             if (nums[mid] >= target) right = mid;             else left = mid + 1;         }         // 此时找到了左边第一个元素 left         if (nums[left] != target)             return res;         res[0] = left;         left = 0;         right = nums.length - 1;         while (left < right) {             //是为了防止当left+1=right的时候 之前是mid=(left+right)/2 2left+1/2=left             //此时mid就一直会是left 一直循环             int mid = left + (right - left+1) / 2;             if (nums[mid] <= target) left = mid;             else right = mid - 1;         }         res[1] = right;         return res;     } }