LC 42.接雨水_业界新闻

42.接雨水

给定n个非负整数表示每个宽度为1的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

输入： height = [0,1,0,2,1,0,1,3,2,1,2,1]

输出： 6

解释： 上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以
接 6 个单位的雨水（蓝色部分表示雨水）。

示例 2：

输入： height = [4,2,0,3,2,5]

输出： 9

提示：

n == h e i g h t . l e n g t h

\leq n \leq 2 * 10^4

\leq height[i] \leq 10^5

解法一(双指针)

思路分析

对于下雨之后能接多少雨水, 取决于凹槽的数量以及每个凹槽的容量; 而凹槽的容量是由左右边界的最小值以及左右边界长度决定的;

可以使用左右指针分别指向数组左右边界, 分别移动左右指针来计算接水量;

当两边柱子有一端更高时, 假设在右端, 如下图所示, 则此时积水的高度依赖于从左到右方向; 计算积水量应该从左到右进行计算; 左端柱子更高时同理;
在这里插入图片描述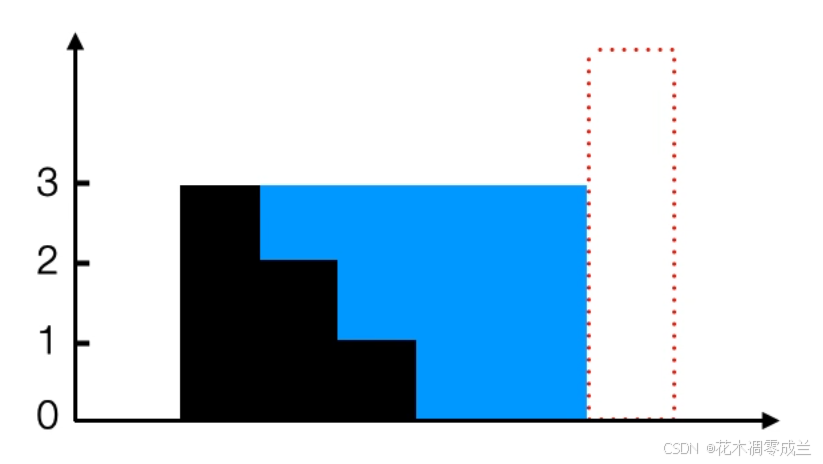

所以在左右指针指向的柱子之间, 若左指针指向的柱子小于右指针指向的柱子, 则应该移动左指针, 反之应该移动右指针;

使用leftMax变量来记录左指针左边柱子的最大值, 当左指针所在柱子高度高于左边柱子最大值时, 说明左指针柱子处无法接到雨水, 则跳过并更新最大值, 且左指针继续向右移动;

同理, 使用rightMax变量记录右指针右边柱子的最大值, 当右指针所在柱子高度高于右边柱子最大值时, 右指针柱子无法接到雨水, 则跳过并更新最大值, 且右指针继续向左移动;

实现代码

class Solution { // 双指针 public int trap(int[] height) { // 初始化 int ans = 0; // 左、右指针分别指向最左边界、最右边界 int left = 0, right = height.length-1; // 左边界最大值 int leftMax = 0; // 右边界最大值 int rightMax = 0; while (left < right) { if (height[left] < height[right]) { // 若左边界高度低于右边界高度则说明凹槽高度以左边界为准 if (height[left] > leftMax) { // 当此时左边界高度大于左边界最大值时无法形成凹槽所以不计算雨水量 // 更新左边界 leftMax = height[left]; } else { // 左边界高度低于最大值则说明该处可以接到雨水计算雨水量 ans += leftMax - height[left]; } // 移动左边界 ++ left; } else { if (height[right] > rightMax) { rightMax = height[right]; } else { ans += rightMax - height[right]; } -- right; } } return ans; } }