*_*课间休息后的知识点轰炸
树状数组
引入
给定长为 n 的序列 a,q 次操作,每次查询一段区间的和,或修改一个数的权值。 1≤n,q≤5×10^5,0≤a_i≤10^9。
分析
如果没有修改操作,这是一道非常简单的前缀和题。 假如我们修改前缀和数组,查询就还是 O(1) 的,是否可行呢? 当然不行。 考虑哪里出了问题。 修改原数组,逐个统计,修改复杂度是 O(1) 的,查询是 O(n)。 修改前缀和数组,修改复杂度 O(n),但查询只有 O(1)。 很明显,有个 O(n) 大头压着,O(1) 复杂度被浪费了。 基于平衡复杂度的思想,我们不妨考虑适当提升低复杂度的部分,以降低高复杂度的部分。
我们提前处理出一些区间的和。 修改时,只需要修改包含这个元素的区间;查询时,把查询区间拆成若干处理好的区间。 现在的问题就是,如何划分区间,使得无论修改哪个元素,查询哪段区间,影响的区间都不会太多。
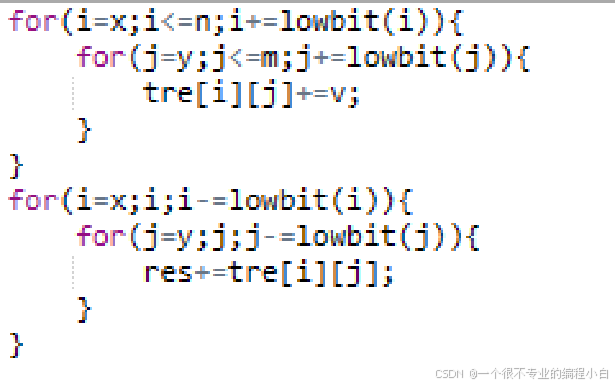
规定正整数 x 的 lowbit(x) 表示 x 的二进制里,最低位的 1 对应数的大小。 比如 lowbit(5)=lowbit(9)=1,lowbit(12)=4。 我们把序列划分成 n 个区间,标号为 k 的区间维护下标 [k-lowbit(k)+1,k] 的区间和。 由于 c++ 对负数存储是取反后加一,lowbit 有一种快速的求法。
int lowbit(int x){ return x&(-x); }我们先放一张图便于理解:
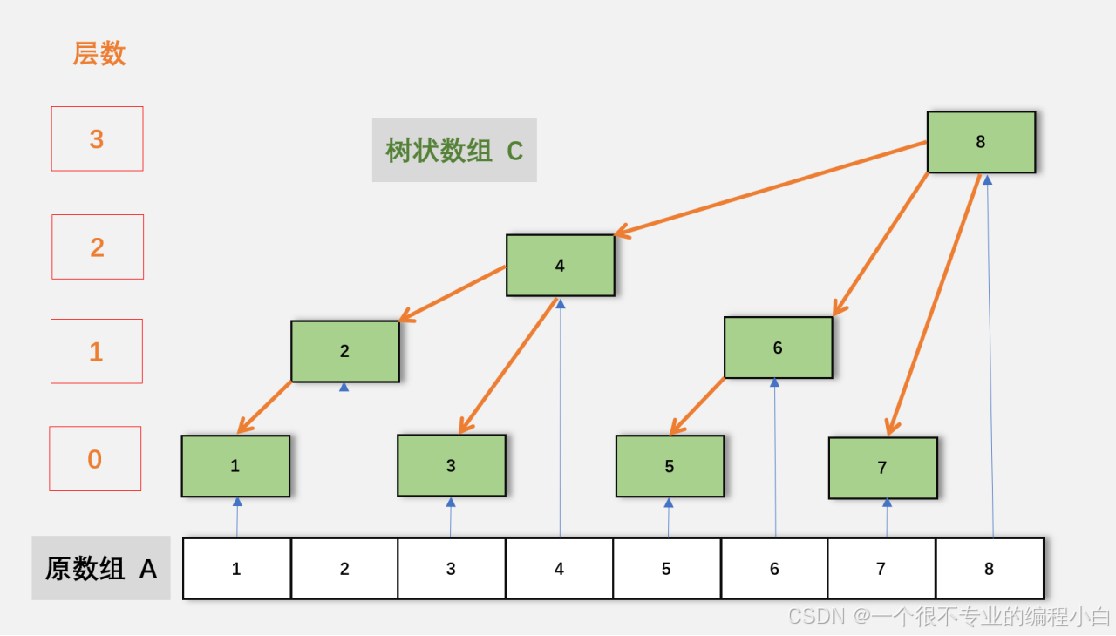
考虑修改 a_k 时,会影响哪些区间。 将修改 a_k 影响的区间编号从小到大排列后,第一项为 k,之后每项为前一项加它的的 lowbit。 因为每加一次,新区间一定是包含原区间的。 树状数组不支持对任意区间进行查询,正常来说只能前缀查询。 和修改类似,查询前缀 1 到 k 时,影响到的区间就是不断减去 lowbit 的那些区间。 这个根据定义看就行。
虽然理论很复杂,但树状数组的代码相当好写
最重要的一点,树状数组常数是1,比线段树快一大截
如果是区间修改、单点查询怎么办? 对原序列差分,变为单点修改、前缀查询的问题。 bonus:区间修改、区间查询怎么做?
树状数组干不了区间修改的活,所以还是先差分变成单点修改。 假设差分数组为 b,查询前缀为 [1,x]。 推导式子如右图。 i×b_i 再用一个树状数组维护即可。
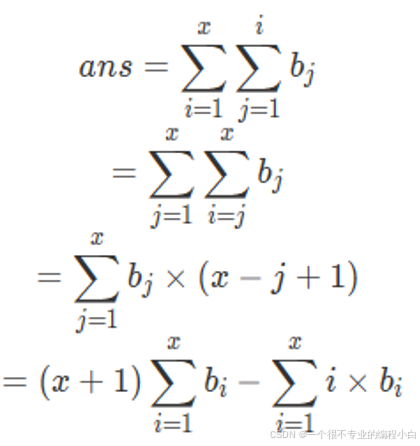
一个数每次减 lowbit 后,其二进制表示里至少会少一个一。 一个数每次加 lowbit 后,新数的 lowbit 至少是原数的二倍。 因此,树状数组修改和查询的复杂度均为 O(logn)。 总复杂度 O(qlogn)。 初始时将原始序列顺次加入即可。
例题讲解
1.P3374 【模板】树状数组 1
AC代码
#include <iostream> #include <cstdio> #include<cmath> #include<algorithm> #include<cstring> using namespace std; const int N=500010; int n,m,i,num[N],t[2*N],l,r; int lowbit(int x){ return x&(-x); } int change(int x,int p){ while(x<=n){ t[x]+=p; x+=lowbit(x); } return 0; } int sum(int k){ int ans=0; while(k>0){ ans+= t[k]; k-=lowbit(k); } return ans; } int ask(int l,int r){ return sum(r)-sum(l-1); } int main(){ scanf("%d%d",&n,&m); for(int i=1;i<=n;i++){ cin>>num[i]; int a=change(i,num[i]); } for(int i=1;i<=m;i++){ int a; scanf("%d%d%d",&a,&l,&r); if(a==2)printf("%d\n",ask(l,r)); else a=change(l,r); } return 0; }2.P3368 【模板】树状数组 2
AC代码
#include <iostream> #include <cstdio> #include<cmath> #include<algorithm> #include<cstring> using namespace std; const int N=500010; long long n,m,num[N],t[2*N],l,r; long long lowbit(long long x){ return x&(-x); } void change(long long x,long long m){ for(long long i=x;i<=n;i+=lowbit(i))t[i]+=m; } long long ask(long long s){ long long ans=0; for(long long i=s;i>=1;i-=lowbit(i))ans+=t[i]; return ans; } int main(){ scanf("%lld%lld",&n,&m); for(long long i=1;i<=n;i++)scanf("%lld",&num[i]); for(long long i=1;i<=m;i++){ int a; scanf("%d",&a); if(a==2){ int o; scanf("%lld",&o); printf("%lld\n",num[o]+ask(o)); } else { long long x,y,s; scanf("%lld%lld%lld",&x,&y,&s); change(x,s); change(y+1,-s); } } return 0; }二维树状数组
给定一个 n*m 的矩阵,单点修改,求子矩阵的和。 和一维的差不多,但这里 tre[x][y] 表示行在 [x-lowbit(x)+1,x],列在 [y-lowbit(y)+1,y] 范围内元素的和。
树状数组如果要对任意区间查询,那么只能查询两个前缀做差。 诸如 min/max 这种不可减的东西,如果要区间查询,是不能用树状数组直接维护的。 当然,如果只前缀查询的话还是没有问题的。 但修改时,min 只能往小了改,max 只能往大了改,否则依旧会出现问题。 虽然有些特殊手段能规避这些问题,但写着会很麻烦。 总之不太建议拿树状数组维护这类东西。
线段树
回到最初的问题。 给定长为 n 的序列 a,q 次操作,每次查询一段区间的和,或修改一个数的权值。 1≤n,q≤5×10^5,0≤a_i≤10^9。 我们刚才通过类似二进制的划分,得到了一个单 log 的解法。 有没有什么别的划分方式,也能实现单 log 呢?
一个很简单粗暴的想法:每次把区间对半劈开。 这样划分就是我们的线段树。 放一张线段树的经典老图。
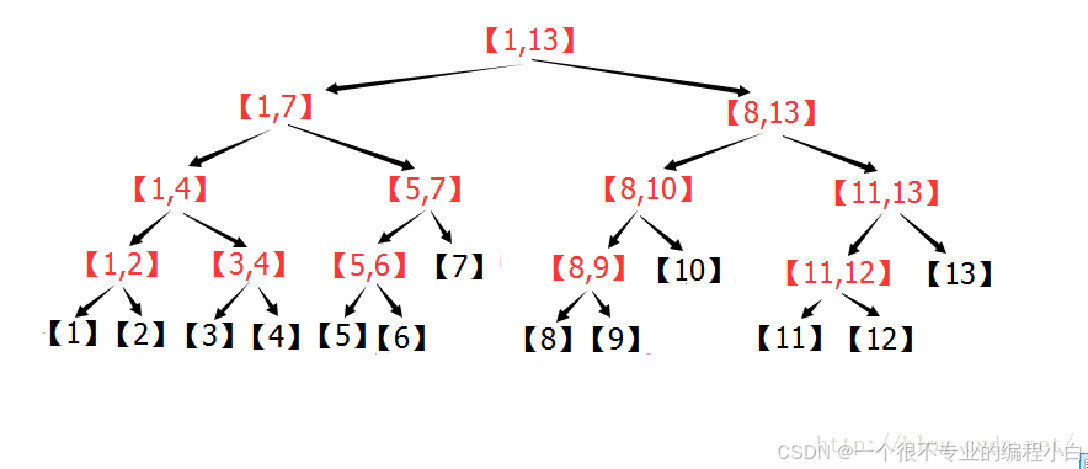
由于区间是对半劈开的,因此每往下一层,区间长度减半。 所以线段树的深度为 logn 级别的。 因此单点修改/求解时,只需访问 O(logn) 个节点即可。 区间查询时,无论是多大的区间,最多会分成 2logn 个线段树上的区间。 假如线段树某一层中有三个区间是结果区间,那么居中的那个区间的父节点对应区间也一定是包含在询问区间内的,因此线段树每一层至多会选中 2 个区间。
由于区间是对半劈开的,因此每往下一层,区间长度减半。 所以线段树的深度为 logn 级别的。 因此单点修改/求解时,只需访问 O(logn) 个节点即可。 区间查询时,无论是多大的区间,最多会分成 2logn 个线段树上的区间。 假如线段树某一层中有三个区间是结果区间,那么居中的那个区间的父节点对应区间也一定是包含在询问区间内的,因此线段树每一层至多会选中 2 个区间。
模板题讲解
1.P3372 【模板】线段树 1
AC代码
#include<iostream> #include<cstdio> #define MAXN 1000001 #define ll long long using namespace std; unsigned ll n,m,a[MAXN],ans[MAXN<<2],tag[MAXN<<2]; inline ll ls(ll x) { return x<<1; } inline ll rs(ll x) { return x<<1|1; } inline void push_up(ll p) { ans[p]=ans[ls(p)]+ans[rs(p)]; } inline void build(ll p,ll l,ll r) { tag[p]=0; if(l==r){ans[p]=a[l];return ;} ll mid=(l+r)>>1; build(ls(p),l,mid); build(rs(p),mid+1,r); push_up(p); } inline void f(ll p,ll l,ll r,ll k) { tag[p]=tag[p]+k; ans[p]=ans[p]+k*(r-l+1); } inline void push_down(ll p,ll l,ll r) { ll mid=(l+r)>>1; f(ls(p),l,mid,tag[p]); f(rs(p),mid+1,r,tag[p]); tag[p]=0; } inline void update(ll nl,ll nr,ll l,ll r,ll p,ll k) { if(nl<=l&&r<=nr) { ans[p]+=k*(r-l+1); tag[p]+=k; return ; } push_down(p,l,r); ll mid=(l+r)>>1; if(nl<=mid)update(nl,nr,l,mid,ls(p),k); if(nr>mid) update(nl,nr,mid+1,r,rs(p),k); push_up(p); } inline ll query(ll q_x,ll q_y,ll l,ll r,ll p) { ll res=0; if(q_x<=l&&r<=q_y)return ans[p]; ll mid=(l+r)>>1; push_down(p,l,r); if(q_x<=mid)res+=query(q_x,q_y,l,mid,ls(p)); if(q_y>mid) res+=query(q_x,q_y,mid+1,r,rs(p)); return res; } int main() { ll a1,b,c,d,e,f; cin>>n>>m; for(ll i=1;i<=n;i++) scanf("%lld",&a[i]); build(1,1,n); while(m--) { scanf("%lld",&a1); if(a1==1){ scanf("%lld%lld%lld",&b,&c,&d); update(b,c,1,n,1,d); } else { scanf("%lld%lld",&e,&f); printf("%lld\n",query(e,f,1,n,1)); } } return 0; }2.P3373 【模板】线段树 2
AC代码
#include <bits/stdc++.h> #define MAXN 100010 #define ll long long using namespace std; int n, m, mod; int a[MAXN]; struct Segment_Tree { ll sum, add, mul; int l, r; }s[MAXN * 4]; inline void update(int pos) { s[pos].sum = (s[pos << 1].sum + s[pos << 1 | 1].sum) % mod; return; } inline void pushdown(int pos) { s[pos << 1].sum = (s[pos << 1].sum * s[pos].mul + s[pos].add * (s[pos << 1].r - s[pos << 1].l + 1)) % mod; s[pos << 1 | 1].sum = (s[pos << 1 | 1].sum * s[pos].mul + s[pos].add * (s[pos << 1 | 1].r - s[pos << 1 | 1].l + 1)) % mod; s[pos << 1].mul = (s[pos << 1].mul * s[pos].mul) % mod; s[pos << 1 | 1].mul = (s[pos << 1 | 1].mul * s[pos].mul) % mod; s[pos << 1].add = (s[pos << 1].add * s[pos].mul + s[pos].add) % mod; s[pos << 1 | 1].add = (s[pos << 1 | 1].add * s[pos].mul + s[pos].add) % mod; s[pos].add = 0; s[pos].mul = 1; return; } inline void build_tree(int pos, int l, int r) { s[pos].l = l; s[pos].r = r; s[pos].mul = 1; if (l == r) { s[pos].sum = a[l] % mod; return; } int mid = (l + r) >> 1; build_tree(pos << 1, l, mid); build_tree(pos << 1 | 1, mid + 1, r); update(pos); return; } inline void ChangeMul(int pos, int x, int y, int k) { if (x <= s[pos].l && s[pos].r <= y) { s[pos].add = (s[pos].add * k) % mod; s[pos].mul = (s[pos].mul * k) % mod; s[pos].sum = (s[pos].sum * k) % mod; return; } pushdown(pos); int mid = (s[pos].l + s[pos].r) >> 1; if (x <= mid) ChangeMul(pos << 1, x, y, k); if (y > mid) ChangeMul(pos << 1 | 1, x, y, k); update(pos); return; } inline void ChangeAdd(int pos, int x, int y, int k) { if (x <= s[pos].l && s[pos].r <= y) { s[pos].add = (s[pos].add + k) % mod; s[pos].sum = (s[pos].sum + k * (s[pos].r - s[pos].l + 1)) % mod; return; } pushdown(pos); int mid = (s[pos].l + s[pos].r) >> 1; if (x <= mid) ChangeAdd(pos << 1, x, y, k); if (y > mid) ChangeAdd(pos << 1 | 1, x, y, k); update(pos); return; } inline ll AskRange(int pos, int x, int y) { if (x <= s[pos].l && s[pos].r <= y) { return s[pos].sum; } pushdown(pos); ll val = 0; int mid = (s[pos].l + s[pos].r) >> 1; if (x <= mid) val = (val + AskRange(pos << 1, x, y)) % mod; if (y > mid) val = (val + AskRange(pos << 1 | 1, x, y)) % mod; return val; } int main() { scanf("%d%d%d", &n, &m, &mod); for (int i = 1; i <= n; i++) { scanf("%d", &a[i]); } build_tree(1, 1, n); for (int i = 1; i <= m; i++) { int opt, x, y; scanf("%d%d%d", &opt, &x, &y); if (opt == 1) { int k; scanf("%d", &k); ChangeMul(1, x, y, k); } if (opt == 2) { int k; scanf("%d", &k); ChangeAdd(1, x, y, k); } if (opt == 3) { printf("%lld\n", AskRange(1, x, y)); } } return 0; }Pushup 是线段树的核心函数,目的是把子节点的信息合并到父节点上。基于不同问题、维护不同信息,pushup 会有不同写法。 Build、modify(change)、query 之类的函数是线段树的功能函数,这些功能函数的写法是相当规矩的。 核心思想就是把目标区间,拆成若干线段树上的区间,整体处理。 这个思想其实很像分治。 分治里也的确有这样的技巧——保留分治每一步的结果,在分治树上进行操作,用于处理修改之类的操作。 但这些都是题外话了。
例题讲解
1.P4513 小白逛公园
格式化题面
给定长为 n 的序列 a,q 次操作。 每次修改序列中的一个数,或是查询一段区间的最大子段和。 区间[l,r]的最大子段和是指,对于所有l≤l_1≤r_1≤r,区间[l_1,r_1]的区间和中,最大的那个。 1≤n,q≤5×10^5,−10^9≤a_i≤10^9。
思路
线段树解决问题,最重要的就是思考如何合并(pushup)能做到高效且不重不漏。 显然最大子段和不一定是两个区间各自最大子段和的最大值。 因为我们少考虑了在两个区间中各有一部分的那些区间。 既然如此,那就将他们考虑进来就好。 由于这些区间左右端点分在两个区间内,所以可以分别独立考虑
每个区间,维护其最大子段和、前缀和最大值、后缀和最大值、区间和。 这样,新区间的最大子段和就是左右区间的最大子段和、左区间后缀和max+右区间前缀和max这三项中取最大一项。 区间和是好维护的。 前缀和max有两种情况,要么是左区间的前缀和max,要么是整个左区间加上右区间的前缀和max。 这也是维护区间和的意义所在。 后缀和max同理。 只要能写出这些东西的 pushup,考虑好修改时对权值的直接影响,修改操作就做完了。
查询也是跑不掉的…… 线段树查询的实质,就是把目标分成若干连续区间,然后再把这些区间信息一一合并。 但有一点好处。 按刚才代码里的写法,查询到区间按顺序刚好是从左往右的。 因此只需要在全局记录后缀最大和以及答案,每次遇到一段区间做类似 pushup 的工作就可以了。
还是太麻烦了,怎么办? 线段树有一个写法上的小技巧。 我们把要维护的信息定义进一个结构体里,然后重载结构体的加法运算。 Pushup 函数只需要像正常维护区间和一样左加右就可以了。 Query 会遇到一点小问题,取决于这个结构体的 0 值如何定义。 定义不了也没关系。 如果只有一半是有用的,直接返回 query(那一半)。否则返回 query(左半)+query(右半)。 由于本题只需要维护这四项,所以直接对整个结构体重载了。(代码里用的不是这种写法)
AC代码
#include<cstdio> #include<algorithm> using namespace std; #define N 500001 struct Node{int ans,lmax,rmax,sum;}tre[N<<2]; inline void pushup(Node &rt,const Node &ls,const Node &rs) { if(ls.rmax<0 && rs.lmax<0) rt.ans=max(ls.rmax,rs.lmax); else { rt.ans=0; if(ls.rmax>0) rt.ans+=ls.rmax; if(rs.lmax>0) rt.ans+=rs.lmax; } rt.ans=max(rt.ans,ls.ans); rt.ans=max(rt.ans,rs.ans); rt.lmax=max(ls.lmax,ls.sum+rs.lmax); rt.rmax=max(rs.rmax,rs.sum+ls.rmax); rt.sum=ls.sum+rs.sum; } inline void build(int rt,int l,int r) { if(l==r) { scanf("%d",&tre[rt].ans); tre[rt].sum=tre[rt].lmax=tre[rt].rmax=tre[rt].ans; return; } int m=(l+r>>1); build(rt<<1,l,m); build(rt<<1|1,m+1,r); pushup(tre[rt],tre[rt<<1],tre[rt<<1|1]); } void update(int p,int v,int rt,int l,int r) { if(l==r) { tre[rt].sum=tre[rt].lmax=tre[rt].rmax=tre[rt].ans=v; return; } int m=(l+r>>1); if(p<=m) update(p,v,rt<<1,l,m); else update(p,v,rt<<1|1,m+1,r); pushup(tre[rt],tre[rt<<1],tre[rt<<1|1]); } Node query(int ql,int qr,int rt,int l,int r) { if(ql<=l&&r<=qr) return tre[rt]; int m=(l+r>>1); if(ql<=m && m<qr) { Node res; pushup(res,query(ql,qr,rt<<1,l,m),query(ql,qr,rt<<1|1,m+1,r)); return res; } else if(ql<=m) return query(ql,qr,rt<<1,l,m); else return query(ql,qr,rt<<1|1,m+1,r); } int n,m; int main() { int op,x,y; scanf("%d%d",&n,&m); build(1,1,n); for(;m;--m) { scanf("%d%d%d",&op,&x,&y); if(op==1) { if(x>y) swap(x,y); printf("%d\n",query(x,y,1,1,n).ans); } else update(x,y,1,1,n); } return 0; }优化
解决区间操作
我们跳过区间加单点查,直接看区间加区间求和线段树如何解决。 线段树的功能比树状数组强很多,完全没必要像树状数组那样开两个处理。
首先,还是把待修改区间拆成若干个目标区间。 直接把修改下放到每个点是会原地爆炸的。 不妨在当前节点打上一个标记,表示这个节点对应的区间内需要加上多少,然后更新该节点的区间和。 这样,从这个点到根节点的权值和都是正确的,仅子树内其他点的权值和是少一部分的。 很明显,当一个区间积累了多个修改操作时,我们可以简单的把标记累加,无需打上多个标记。 只要没有访问到子树内部节点,这样做肯定是正确的。 但当访问到子树内的节点时,基于对标记的不同处理方法,衍生出两个分支。
标记下方
非叶节点的标记本质上是一个没有下放完全的操作。 既然如此,那么从上往下访问到某个节点的时候,将它上面的标记下放给左右儿子即可。 这就是 pushdown 函数。 只需要干三件事: 1. 更新左右儿子的信息。 2. 将当前节点的标记累加给左右儿子。 3. 清空当前节点的标记。 由于维护的是区间和,需要额外记录区间长度。 初始化时顺带记录即可。

标记永久化
标记永久化使用范围略窄,但偏偏能干一些标记下放不好做/做不了的事。 我们额外准备一个计数器,初值为 0。当遇到一个标记时,将其累加进计数器里。这个计数器,就表示当前区间还应加上多少数(或一些其他的东西)。 这样,修改操作什么多余的也不用干。不过子树加的东西可能会影响到自身,所以 pushup 操作要额外加上自身 tag*len。 查询操作查到目标区间时,额外加上计数器乘区间长度即可。 但由于当前节点的标记已经更新了该节点,所以不能算入这部分。


解决区间乘问题
很明显我们需要再打上一个乘法标记。 标记永久化的缺点很明显,它不太好处理多个标记之间的关系。 所以采用标记下放。 乘法标记叠加,以及乘法标记对区间和的影响,都是累乘就行,那加法标记呢? 我们给标记规定下顺序:先乘后加。 下放时,乘法标记先对子节点的加法、乘法标记和区间和累乘。 加法标记再累加给加法标记、区间和。 修改时,加法标记照常,乘法标记对该区间的三项累乘。 为什么父亲的加法标记不用乘上儿子的乘法标记?
考虑 pushdown 的过程。如果儿子的标记是后打上的,此时父亲不应有标记。 因此这个父亲的加法标记是后来的,自然不会受子节点的乘法标记影响。 为了简化代码,依旧建议,把对一个节点打乘法标记单独写出一个函数。在修改和下放中都会用到。

 动态开点
动态开点
有一个长度为 n 的序列 a,初始 a_i=i。 q 次操作,单点加,或者查询一段区间的和。 n≤10^9,q≤3×10^5。 如果不看 n 的范围,这是一道相当基础的线段树入门题。 但 n 是相当庞大的,甚至不能支持初始遍历一遍线段树。 该怎么办呢?
首先 ai=i 的初值是完全没用的。查询时额外套公式加上就行。 只需要考虑对一个全为 0 的序列,单点修改、区间查询就行。 关注到相对于 n,q 非常小。 也就是说,即使所有的操作全用来单点修改了,不为 0 的叶子节点顶天只有 q 个。 对于那些区间内全为 0 的空节点,我们根本没必要去记录。查询遇到这种空节点时,直接返回 0 就行。
因此,我们进行这样的处理: 1. 线段树区间管辖范围依旧为 1 到 n,但不进行初始化。 2. 插入一个节点时,按正常流程走下去。走到一个空节点时,把这个节点“建出来”,赋予其一个非 0 的编号。 3. 查询也按正常流程走,走到一个空节点时,直接返回 0。 只有插入过程会新建节点,单次插入至多新建 logn个节点。 因此,动态开点线段树的空间要开到 qlogn。 实战经验是,开不死就往死里开。3e7……
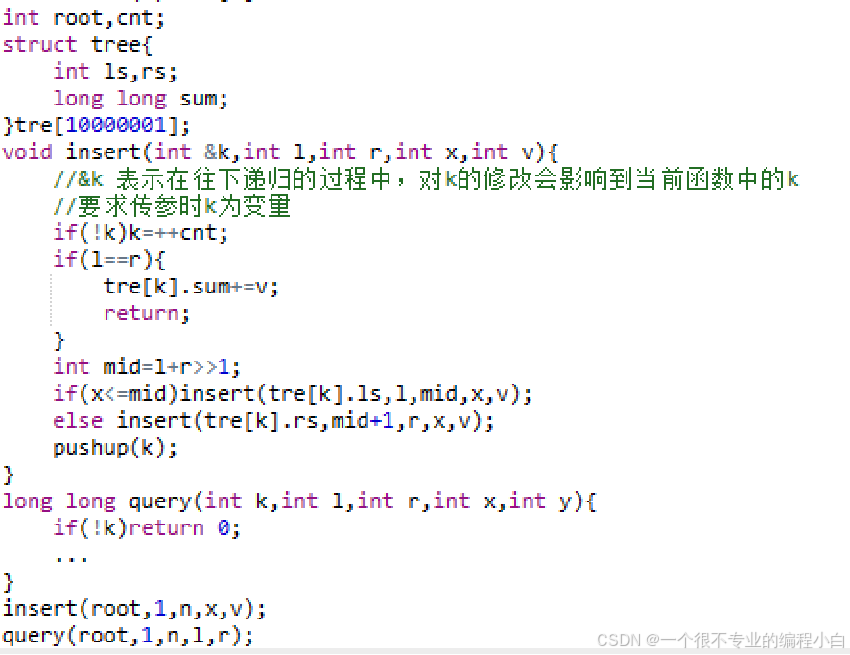
动态开点线段树同样能做区间修改,方法也是类似的。 很显然,使用标记永久化比标记下放好多了,还能省相当多的空间。
线段树优化其他算法
莫队二次离线就需要数据结构来维护,线段树就能够胜任这一任务
此外,扫描线算法也需要线段树来维护
扫描线一般运用在图形上面,它和它的字面意思十分相似,就是一条线在整个图上扫来扫去,它一般被用来解决图形面积,周长,以及二维数点等问题。
1.P5490 【模板】扫描线
AC代码
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> using namespace std; #define ls (rt << 1) #define rs (rt << 1 | 1) long long n, x1, x2, y1, y2, x, y, rk[2097152], val[2097152], cnt, maxn = 1 << 31; struct Segment_tree { long long l, r; long long cnt, len; }t[2097152]; struct node { long long x, yh, yl, flag; }e[2097152]; inline void pushup(long long rt) { if ((t[rt].l == maxn && t[rt].r == maxn)) return; if (t[rt].cnt) t[rt].len = val[t[rt].r + 1] - val[t[rt].l]; else t[rt].len = t[ls].len + t[rs].len; } inline void build(long long rt, long long l, long long r) { t[rt].l = l, t[rt].r = r; if (l == r) return; long long mid = (t[rt].l + t[rt].r) >> 1; build(ls, l, mid); build(rs, mid + 1, r); } inline void add(long long rt, long long l, long long r, long long v) { if (l <= t[rt].l && t[rt].r <= r) { t[rt].cnt += v; pushup(rt); return; } long long mid = (t[rt].l + t[rt].r) >> 1; if (l <= mid) add(ls, l, r, v); if (mid < r) add(rs, l, r, v); pushup(rt); } inline bool cmp(node a, node b) { if (a.x != b.x) return a.x < b.x; return a.flag > b.flag; } int main() { cin >> n; long long ans = 0; for (long long i = 1; i <= n; i++) { scanf("%lld%lld%lld%lld", &x1, &y1, &x2, &y2); e[(i << 1) - 1].x = x1, e[i << 1].x = x2; e[(i << 1) - 1].yh = e[i << 1].yh = y2; e[(i << 1) - 1].yl = e[i << 1].yl = y1; e[(i << 1) - 1].flag = 1, e[i << 1].flag = -1; rk[++cnt] = y1; rk[++cnt] = y2; } sort(rk + 1, rk + (n << 1) + 1); cnt = unique(rk + 1, rk + (n << 1) + 1) - rk - 1; for (long long i = 1; i <= 2 * n; i++) { long long pos1 = lower_bound(rk + 1, rk + cnt + 1, e[i].yh) - rk; long long pos2 = lower_bound(rk + 1, rk + cnt + 1, e[i].yl) - rk; val[pos1] = e[i].yh; val[pos2] = e[i].yl; e[i].yh = pos1; maxn = max(maxn, pos1); e[i].yl = pos2; } sort(e + 1, e + 2 * n + 1, cmp); build(1, 1, n << 1); for (long long i = 1; i < n << 1; i++) { add(1, e[i].yl, e[i].yh - 1, e[i].flag); ans += t[1].len * (e[i + 1].x - e[i].x); } cout << ans << endl; return 0; }2.P3373 【模板】线段树 2
AC代码
#include <bits/stdc++.h> #define MAXN 100010 #define ll long long using namespace std; int n, m, mod; int a[MAXN]; struct Segment_Tree { ll sum, add, mul; int l, r; }s[MAXN * 4]; inline void update(int pos) { s[pos].sum = (s[pos << 1].sum + s[pos << 1 | 1].sum) % mod; return; } inline void pushdown(int pos) { s[pos << 1].sum = (s[pos << 1].sum * s[pos].mul + s[pos].add * (s[pos << 1].r - s[pos << 1].l + 1)) % mod; s[pos << 1 | 1].sum = (s[pos << 1 | 1].sum * s[pos].mul + s[pos].add * (s[pos << 1 | 1].r - s[pos << 1 | 1].l + 1)) % mod; s[pos << 1].mul = (s[pos << 1].mul * s[pos].mul) % mod; s[pos << 1 | 1].mul = (s[pos << 1 | 1].mul * s[pos].mul) % mod; s[pos << 1].add = (s[pos << 1].add * s[pos].mul + s[pos].add) % mod; s[pos << 1 | 1].add = (s[pos << 1 | 1].add * s[pos].mul + s[pos].add) % mod; s[pos].add = 0; s[pos].mul = 1; return; } inline void build_tree(int pos, int l, int r) { s[pos].l = l; s[pos].r = r; s[pos].mul = 1; if (l == r) { s[pos].sum = a[l] % mod; return; } int mid = (l + r) >> 1; build_tree(pos << 1, l, mid); build_tree(pos << 1 | 1, mid + 1, r); update(pos); return; } inline void ChangeMul(int pos, int x, int y, int k) { if (x <= s[pos].l && s[pos].r <= y) { s[pos].add = (s[pos].add * k) % mod; s[pos].mul = (s[pos].mul * k) % mod; s[pos].sum = (s[pos].sum * k) % mod; return; } pushdown(pos); int mid = (s[pos].l + s[pos].r) >> 1; if (x <= mid) ChangeMul(pos << 1, x, y, k); if (y > mid) ChangeMul(pos << 1 | 1, x, y, k); update(pos); return; } inline void ChangeAdd(int pos, int x, int y, int k) { if (x <= s[pos].l && s[pos].r <= y) { s[pos].add = (s[pos].add + k) % mod; s[pos].sum = (s[pos].sum + k * (s[pos].r - s[pos].l + 1)) % mod; return; } pushdown(pos); int mid = (s[pos].l + s[pos].r) >> 1; if (x <= mid) ChangeAdd(pos << 1, x, y, k); if (y > mid) ChangeAdd(pos << 1 | 1, x, y, k); update(pos); return; } inline ll AskRange(int pos, int x, int y) { if (x <= s[pos].l && s[pos].r <= y) { return s[pos].sum; } pushdown(pos); ll val = 0; int mid = (s[pos].l + s[pos].r) >> 1; if (x <= mid) val = (val + AskRange(pos << 1, x, y)) % mod; if (y > mid) val = (val + AskRange(pos << 1 | 1, x, y)) % mod; return val; } int main() { scanf("%d%d%d", &n, &m, &mod); for (int i = 1; i <= n; i++) { scanf("%d", &a[i]); } build_tree(1, 1, n); for (int i = 1; i <= m; i++) { int opt, x, y; scanf("%d%d%d", &opt, &x, &y); if (opt == 1) { int k; scanf("%d", &k); ChangeMul(1, x, y, k); } if (opt == 2) { int k; scanf("%d", &k); ChangeAdd(1, x, y, k); } if (opt == 3) { printf("%lld\n", AskRange(1, x, y)); } } return 0; }总结
线段树和树状数组,是 oi 届里最基础,也是最常用的数据结构。 树状数组功能较少,但其码量小、易调试、常数小等优点决定了其在 oi 里卓越的性价比。 线段树是一个相当优秀的数据结构,除了码量偏大外几乎没有缺点。只要信息是可加的,基本都可以靠线段树进行维护。 线段树还有很多重要的延伸,其难度就不在今天的范围内了。 数据结构的精髓并不是代码如何实现、功能多么强大,而是知道如何利用数据结构来解决问题。 不断对问题转化,将问题转化成一些可用数据结构维护的东西,才是数据结构考察的点。
这是我的第十一篇文章,如有纰漏也请各位大佬指正
辛苦创作不易,还望看官点赞收藏打赏,后续还会更新新的内容。
