快速排序（下）

快速排序（下）

前言

在上一篇文章中我们了解了快速排序算法，但那是Hoare的版本，其实还有别的版本：一种是挖坑法，它们的区别主要在于如何找基准值。霍尔的版本思路难理解但代码好理解，挖坑法则是思路好理解但代码不好理解；还有一种是lomuto的前后指针法。
此外，还有不使用递归的快排方法（找基准值还是用的三种方法之一）。

本文就来讲解这几种不同的快排方法。

正文

挖坑法

实现思路：

创建左右指针。首先从右向左找出比基准值小的数据，找到后立即放入左边坑中，当前位置变为新的“坑”，然后从左向右找出比基准值大的数据，找到后立即放入右边坑中，当前位置变为新的“坑”，结束循环后将最开始存储的分界值放入当前的“坑”中，返回当前“坑”的下标（即分界值下标）。

画图理解一下什么是“坑”。

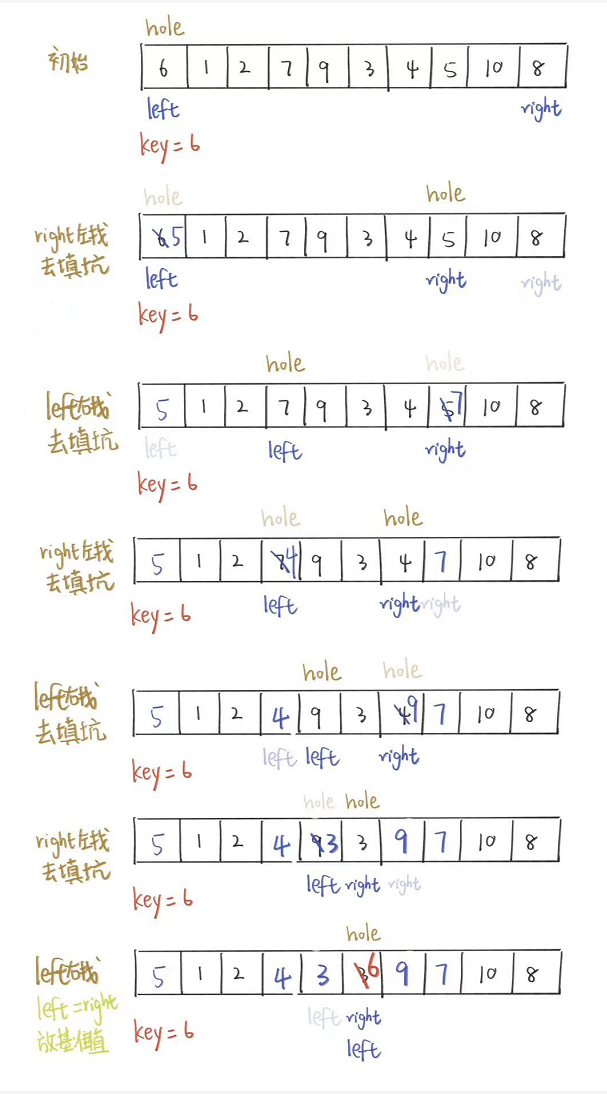
这就是整个“挖坑”然后“填坑”直到left和right重叠时将基准值放到该位置（它该待的位置）的过程。

现在我们可以来写一下挖坑法的代码：

//挖坑法 int _QuickSort(int* arr, int left, int right) { 	int hole = left; 	int key = arr[hole];  	while (left < right)//注意和霍尔版区别 	{ 		//这里同样需要限制且不能是arr[right] >= key，否则可能无法“二分”，最终效率低下 		while (left < right && arr[right] > key) 		{ 			--right; 		} 		arr[hole] = arr[right]; 		hole = right; 		while (left < right && arr[left] < key) 		{ 			++left; 		} 		arr[hole] = arr[left]; 		hole = left; 	} 	arr[hole] = key; 	return hole; } 

排序效果

我们在main函数中写这样的代码：

	int a[] = { 5, 3, 9, 6, 2, 4, 7, 1, 8 }; 	int n = sizeof(a) / sizeof(int); 	printf("排序前: "); 	PrintArr(a, n);//代码不具体展示  	QuickSort(a, 0, n-1);  	printf("排序后: "); 	PrintArr(a, n); 

执行结果：

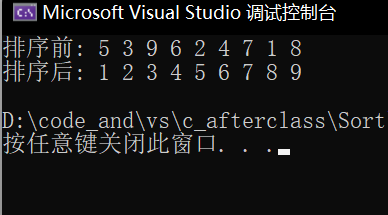
可以看到我们就成功排序了。

---

lomuto前后指针法

实现思路：

创建前后指针，从左往右找比基准值小的进行交换，使得小的都排在基准值的左边。

其实前后指针对于很多学过数据结构的人来说应该已经不陌生了，但是快排也能用到前后指针法，我们看看具体怎么做：

• 定义两个变量prev和cur，让cur指向位置的数据和key值比较
  1. 若arr[cur]<arr[key]，prev向后走一步并和cur交换
  2. 若arr[cur]>=arr[key]，cur继续往后
• 退出循环后将prev与key值交换，找到基准值

同样不变的思路也是要找基准值，也就是要让基准值左侧的数据都小于基准值，让基准值右侧的数据都大于基准值。

那么两个变量的作用是什么？可以说prev是用来占坑的，而cur用来找小，找到小后就让prev加一后和cur交换。退出循环后将prev与key值交换，就找到了基准值。

代码：

//lomuto前后指针法 int _QuickSort(int* arr, int left, int right) { 	int prev = left, cur = left + 1; 	int key = left;  	while (cur<=right) 	{ 		if (arr[cur] < arr[key] && ++prev !=cur)             //prev和cur相同就不交换             //写为arr[cur] <= arr[key]，加上等号也是殊途同归 		{ 			Swap(&arr[cur], &arr[prev]); 		} 		cur++;//进不进循环cur都要往后走 	} 	Swap(&arr[key], &arr[prev]);  	return prev; } 

执行效果：

也一样成功排序完了。

可以发现这一种方法比起前面的Hoare版本和挖坑法，在取不取等号的探讨上少了很多麻烦。

• 注意：

  在循环内的if语句中arr[cur] < arr[key]如果写为arr[cur] <= arr[key]，并不能解决无法”二分“子序列的问题，所以加不加都无所谓。

  这也就是前后指针法的一个**缺陷：如果数组中数据都相等**，效率就会很低。

---

快排的非递归版本

所以现在已经知道了三种版本的快排，其实也就是三种找基准值的方法。

既然我们的快排使用的是递归，就难免有空间上的缺陷。其实快排还有非递归版本。但是要借助数据结构：栈。

那么现在问题是左右区间再分左右区间时我们怎么找区间呢？因为找基准值时没有使用递归而是在找区间时使用的递归（所以找基准值使用前面说的三种方法的任意一种都行）。

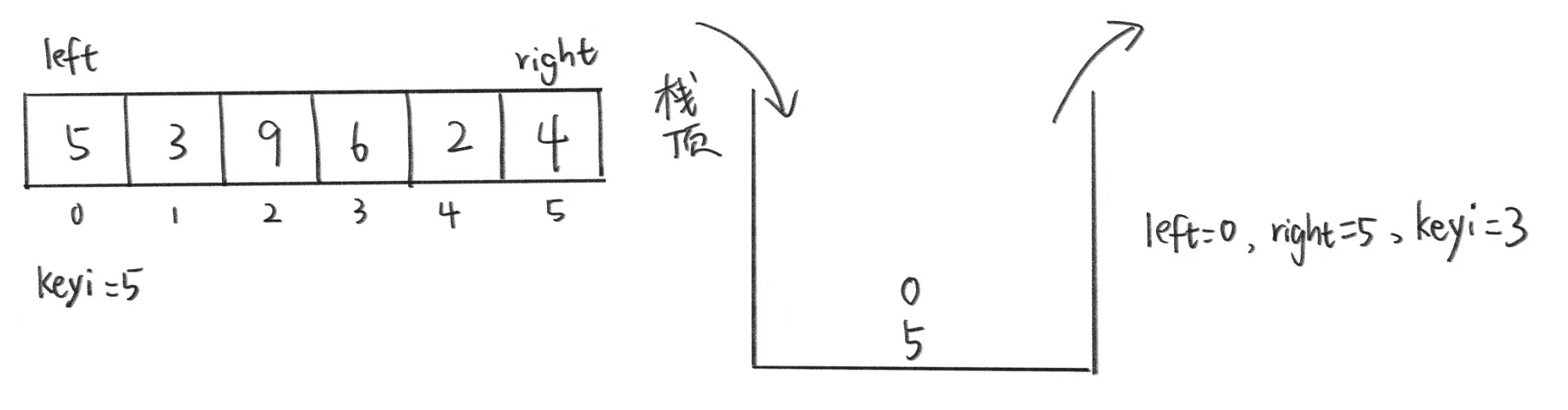
(先将5和0入栈，然后出栈，left=0,right=5，找到基准值为3)

我们知道keyi（基准值）也就能区分左区间和右区间，这两个区间任意哪一个入栈都行。

现在，我们还是一样要现将right入栈再将left入栈（先入右区间），然后再入另一个区间。

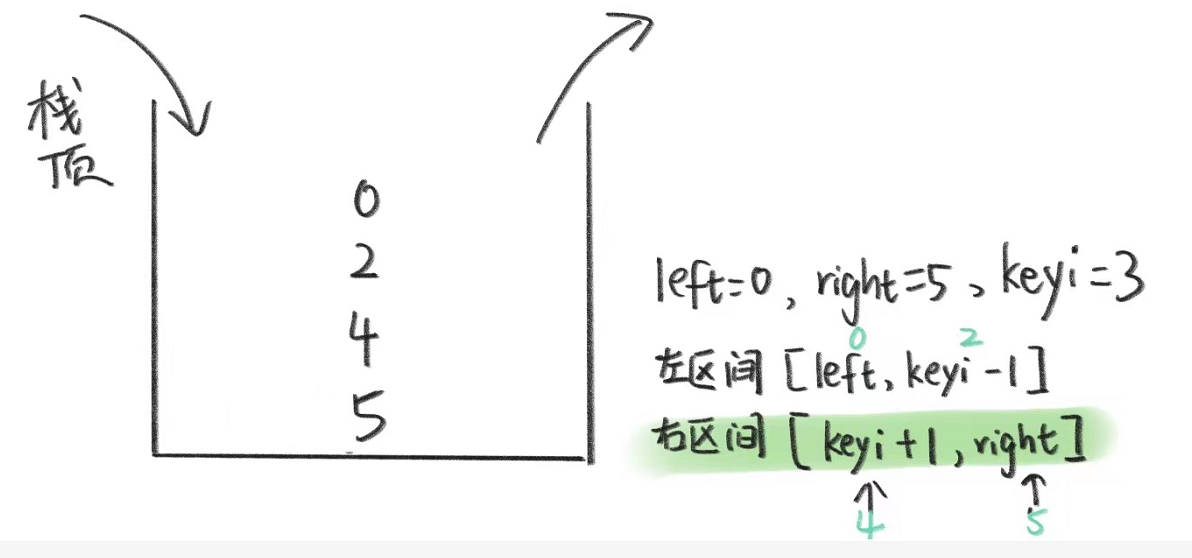
此时栈不为空，我们出栈，先出的两个就是左区间，然后去找它的基准值。

然后这样找下去直到right小于left或等于left时，也就是没有数据或者只有一个数据时，构不成有效区间，就不入栈。

左区间所有基准值找完后，就像二叉树一样，开始走右区间。

开始走右区间时也就是刚好栈里剩的两个数据为右区间时。

所以可以看出，我们取栈顶元素就是在模拟递归。

代码参考

现在我们通过代码来看看怎么使用栈进行快排。

//非递归版快排 //借助数据结构——栈 void QuickSortNonR(int* arr, int left, int right) { 	ST st; 	STInit(&st); 	StackPush(&st, right); 	StackPush(&st, left);  	while (!StackEmpty(&st)) 	{ 		//取两次栈顶 		int begin = StackTop(&st); 		StackPop(&st);  		int end = StackTop(&st); 		StackPop(&st);  		//找基准值——用双指针法 		int prev = begin; 		int cur = begin + 1; 		int keyi = begin;  		while (cur <= end) 		{ 			if (arr[cur] <= arr[keyi] && ++prev!=cur) 			{ 				Swap(&arr[cur], &arr[prev]);  			} 			cur++; 		} 		Swap(&arr[keyi], &arr[prev]);  		keyi = prev; 		//根据基准值划分左右区间 		//左区间：[begin,keyi-1] 		//右区间：[keyi+1,end]  		if (keyi + 1 < end)//控制区间有效 		{ 			StackPush(&st, end); 			StackPush(&st, keyi + 1); 		}	 		if (keyi-1>begin)//控制区间有效 		{ 			StackPush(&st, keyi - 1); 			StackPush(&st, begin); 		} 	}  	STDestroy(&st); } 

那么到此本文就结束了，祝学习愉快=_=