⌈ 传知代码 ⌋ 基于矩阵乘积态的生成模型_业界新闻

发布时间:2024-08-03 03:22

阅读量:0

💛前情提要💛

本文是传知代码平台中的相关前沿知识与技术的分享~

接下来我们即将进入一个全新的空间，对技术有一个全新的视角~

本文所涉及所有资源均在传知代码平台可获取

以下的内容一定会让你对AI 赋能时代有一个颠覆性的认识哦！！！

以下内容干货满满，跟上步伐吧~

📌导航小助手📌
💡本章重点
🍞一. 概述
🍞二. 方法
🍞三.实现
🍞四.训练结果
🫓总结

💡本章重点

基于矩阵乘积态的生成模型

🍞一. 概述

生成模型，通过从数据中学习联合概率分布并据此生成样本，是机器学习和人工智能中的一个重要任务。受量子物理学中概率解释的启发，该文章提出了一种使用矩阵积状态的生成模型，这是一种最初用于描述（特别是一维）纠缠量子态的张量网络。其模型享有类似于密度矩阵重正化群方法的高效学习能力，该方法允许动态调整张量的维度，并提供了一种高效的直接采样方法用于生成任务。本文试图复现该文章的工作，利用该文章的思想，方法去实现MNIST手写数字的生成任务。

Han Z-Y, Wang J, Fan H, et al. Unsupervised Generative Modeling Using Matrix Product States[J]. Physical Review X, 2018, 8(3): 031012

🍞二. 方法

量子力学的概率解释自然地建议使用量子态来建模数据分布。假设我们将概率分布编码到一个量子波函数：

又在一定程度上能够表示更多不同种类的构型成为现在需要解决的问题。许多已经开发的表示方法和算法可以用于高效的概率建模。在这里，我们使用矩阵积状态（MPS）对波函数进行参数化：

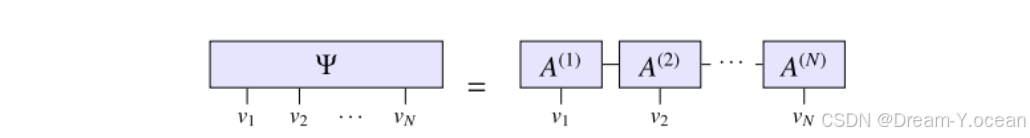
上面的图示意思为，左边是我们需要表示的波函数，线代表它依赖的指标（或者变量），右边则是对应的MPS表示，两个方括号直接的连线代表求和，即将对应的指标（或者变量求和，类似于矩阵的乘积）进行收缩。我们可以看出我们把一个复杂的波函数变成了有限个3指标张量的收缩。

🍞三.实现

导入训练集（MNIST）

1000 张 MNIST 图像已存储为 mnist784_bin_1000.npy。

每张图像包含：n = 28 * 28 个像素，每个像素的取值为0或1。每张图像被视为维度为 2^n 的希尔伯特空间中的一个乘积态。

n = 784  m = 1000 data = np.load("mnist784_bin_1000.npy").astype(np.int32) data = data[:m,:] data = torch.LongTensor(data)\ plt.figure(figsize=(10,2)) imgs = data.cpu().reshape([-1,28,28]) _, ax = plt.subplots(2,10) for i in range(2):      for j in range(10):         index = i * 2 + j         if(a >= imgs.shape[0]):             break         ax[i][j].imshow(imgs[index,:,:],cmap='bone')         ax[i][j].set_xticks([])         ax[i][j].set_yticks([]) plt.show()

这可以让我们观察以下MNIST数据集的样子

定义MPS

现在我们要构造一个初始的MPS, 根据上面的阐述，我们的MPS是由一系列3指标的张量的所构成的，如下所示：

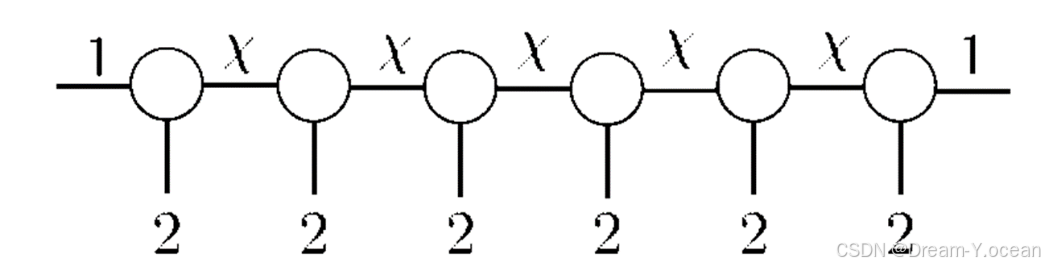
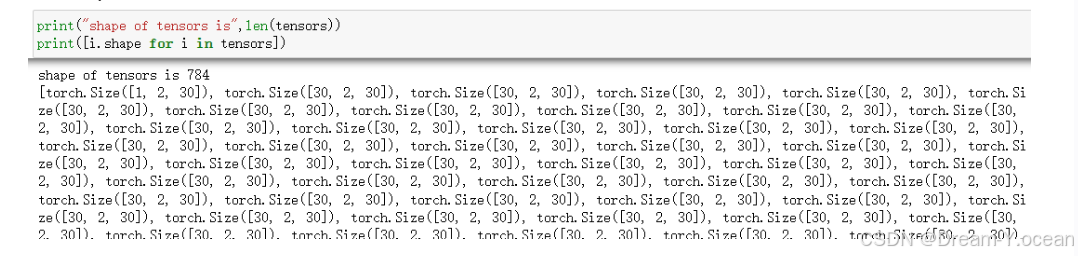
chi = 30  mydevice = 'cuda' if torch.cuda.is_available() else torch.device("cpu") print(mydevice) data = data.to(mydevice) bond_dims = [chi for i in range(n-1)]+[1] tensors= [ torch.randn(bond_dims[i-1],2,bond_dims[i],device=mydevice) for i in range(n)]

我们可以输出从而看到这些张量的输出维度

概率计算

概率计算可以遵循前面的Born公式，即：

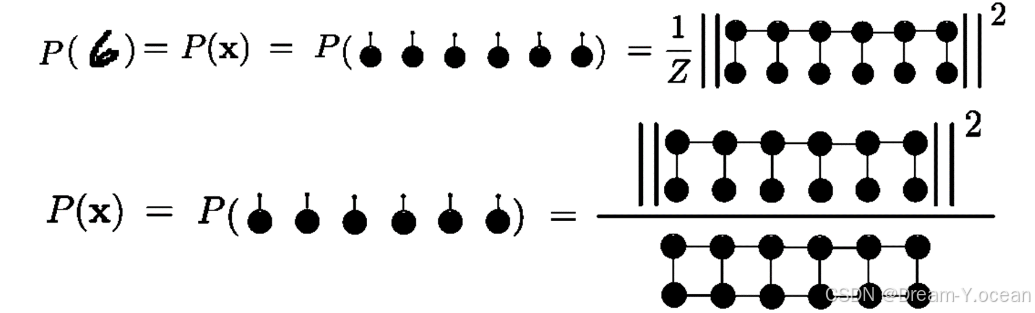
在这里，带有一个小边（常称之为脚）是一个向量，代表的是对应像素的状态，是一个二维向量，用来表示对应的像素是黑还是白

现在难以计算的是配分函数，即：

这个东西，这涉及到张量网络的缩并，在张量网络这个领域中由非常多的缩并方式，一个常用的方法是正交化，即把MPS右边的那些三阶张量全部正交化使得他们收缩刚好是一个单位张量。这个过程如下：

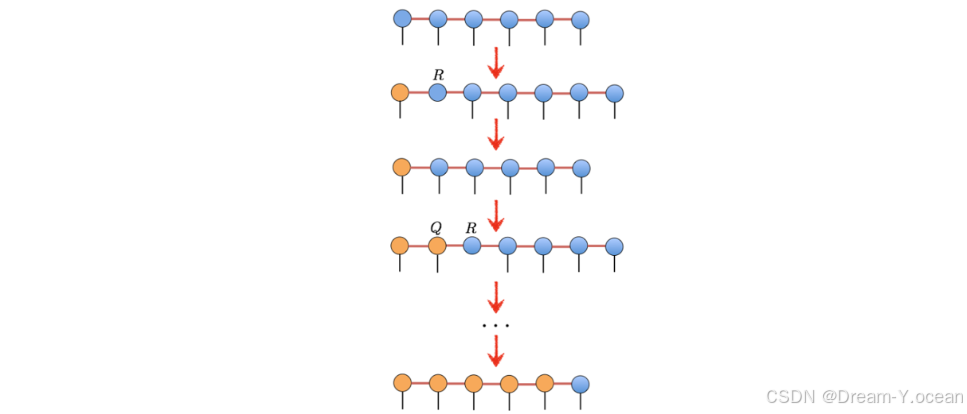
通过不断的对左边的张量作用QR分解从而使得左边张量全部正交化（黄色的）。据此我们可以计算出对应的波函数：

def getPsi():     psi = torch.ones([m, 1, 1], device=mydevice)     for site in range(n):         selected_tensor = tensors[site][:, data[:, site], :].permute(1, 0, 2)         psi = torch.matmul(psi, selected_tensor)     return psi

生成图片

生成图片的过程可以采用条件概率的方法，即先采样一个边缘概率，再从这个边缘概率对应的变量继续采样，重复这个过程即可：

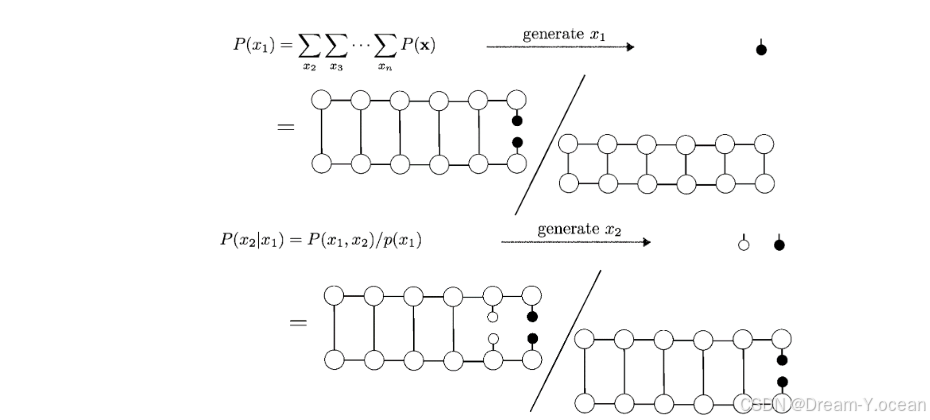
核心代码为：

def generateSamples(batch):     n = 784     samples = torch.zeros([batch, n],device=mydevice)     for site in range(n - 1):         orthogonalize(site, True)      for s in range(batch):         vec = torch.ones(1,1,device=mydevice)         for site in range(n-1, -1, -1):             vec = (tensors[site].view(-1, bond_dims[site]) @ vec).view(-1, 2)             p0 = vec[:, 0].norm()**2 / (vec.norm()**2)             x = (0 if np.random.rand() < p0 else 1)             vec = vec[:, x]             samples[s][site] = x     return samples