
个人主页:欢迎来到 Papicatch的博客
课设专栏 :学生成绩管理系统
专业知识专栏: 专业知识

文章目录
🍉引言
人工智能搜索技术是当今信息技术领域的一项重要突破。它利用了机器学习、自然语言处理和大数据分析等先进技术,为用户提供更加智能、高效和精准的搜索体验。
在传统的搜索技术中,用户需要输入准确的关键词来获取相关信息,但往往难以准确表达自己的需求,导致搜索结果不尽人意。而人工智能搜索技术能够理解用户的自然语言输入,甚至能够根据上下文和用户的历史搜索行为来推测用户的真正意图。
🍈介绍
人工智能搜索是一种将人工智能技术应用于信息检索和查找过程的方法。
它的核心在于利用智能算法和模型,理解用户的需求,并从大量的数据中快速、准确地找到最相关和有用的信息。
与传统的搜索方式相比,人工智能搜索不仅仅依赖于关键词匹配,而是能够深入理解用户输入的自然语言的含义和意图。
例如,如果用户输入“适合老年人的轻便运动方式”,传统搜索可能仅仅基于关键词给出一些包含这些词汇的页面,但人工智能搜索能够理解“老年人”“轻便”“运动方式”等关键元素的综合含义,提供诸如太极、散步、广场舞等更为精准和符合需求的结果。
人工智能搜索还会考虑用户的上下文和历史行为。比如说,如果用户经常搜索与健康养生相关的内容,那么当他再次进行搜索时,系统会更倾向于提供与此类主题相关的结果。
其工作原理通常包括以下几个关键步骤:
- 自然语言处理:将用户输入的文本转换为机器能够理解的形式,并提取关键信息。
- 知识图谱和语义理解:利用知识图谱来理解词语之间的关系,从而更准确地把握用户需求。
- 搜索算法和模型:通过各种智能算法,如深度学习算法、强化学习算法等,在大规模的数据中进行搜索和筛选。
- 结果排序和推荐:根据相关性、用户偏好、信息质量等多种因素,对搜索结果进行排序和推荐。
🍉状态空间法
🍈状态空间的构成
- 状态空间法是一种用于解决问题和描述系统行为的重要方法。
- 它将问题的可能状态以及导致状态之间转换的操作或动作进行建模和表示。
- 状态是对问题在某一时刻的完整描述,包括了问题中所涉及的各种变量的值。例如,在一个机器人路径规划问题中,机器人的位置、方向、电池电量等都可以构成状态的一部分。
- 操作则是能够改变状态的动作或行为。比如机器人的向前移动、向左转、向右转等操作可以改变其位置和方向状态。
- 状态空间可以用一个图来表示,其中节点表示状态,边表示状态之间的转换,也就是操作的结果。
- 通过构建状态空间图,我们可以对问题进行系统的分析和求解。
- 例如,在一个八数码谜题中,初始状态是数字的一种排列,目标状态是数字按特定顺序的排列。我们可以定义移动数字的操作,然后通过在状态空间中搜索从初始状态到目标状态的路径来解决问题。
🍍状态
- 在状态空间中,状态是对问题在特定时刻的完整描述。它包含了问题中所涉及的各种要素和变量的具体取值。
- 例如,在一个下棋的场景中,棋盘上棋子的布局就是一种状态。每个棋子所在的位置、颜色等信息共同构成了这一时刻下棋的状态。
- 再比如,在机器人导航问题中,机器人的位置坐标、朝向、速度等参数的组合就是一个状态。
- 状态能够清晰地反映出问题在某一时刻的具体情况,是后续进行分析和决策的基础。
🍍算符
- 算符是用于改变状态的操作或动作。
- 以魔方为例,旋转魔方的某个面就是一种算符。它会使魔方从一个状态转变为另一个状态。
- 在物流配送问题中,选择不同的配送路线或运输方式可以视为算符,这些操作会改变货物的运输状态。
- 算符具有明确的规则和效果,它们定义了状态之间的可能转换。
🍍问题的解
- 问题的解在状态空间中通常是指从初始状态到目标状态的一系列算符的组合。
- 假设我们要在一个迷宫中找到出口,从起始点所在的状态开始,通过一系列的移动(如向前、向左、向右等算符),最终到达出口所在的状态,这一系列的移动步骤就是问题的解。
- 又如在数学优化问题中,通过一系列的计算步骤(算符),使得目标函数达到最优值,这些计算步骤的组合就是问题的解。
- 需要注意的是,可能存在多个解的情况,而最优解则是在满足一定条件下(如最短路径、最小成本等)最好的那个解。
🍈表示问题的步骤
🍍确定问题的初始状态
- 这是对问题起点的精确描述。需要仔细观察和分析问题开始时的所有相关特征和条件。例如,在一个机器人寻路的问题中,初始状态可能包括机器人的起始位置坐标、周围环境的初始布局、机器人的初始能量水平等。要确保初始状态的描述足够详细和准确,不遗漏任何对后续分析有重要影响的因素。
- 举例:在一个仓库货物搬运的问题中,初始状态可能是货物的初始摆放位置、搬运机器人的初始位置以及仓库中通道的初始畅通情况。
🍍明确问题的目标状态
- 目标状态是问题期望达到的最终结果。它应该是清晰、具体且可衡量的。对于复杂的问题,可能需要将目标分解为多个子目标。例如,在一个拼图游戏中,目标状态就是所有拼图块正确地组合在一起形成完整的图像。
- 举例:在一个生产流程优化的问题中,目标状态可能是在规定时间内以最低成本生产出一定数量且质量合格的产品。
🍍定义状态的描述方式
- 选择合适的方法来准确表示问题中的每个状态。这可能涉及到对数据结构和数学模型的选择。状态描述应该能够捕捉到问题的关键特征,并且便于后续的操作和比较。例如,可以使用向量、矩阵、图结构或者对象等数据结构来表示状态。
- 举例:对于一个棋局问题,可以用一个二维数组来表示棋盘上棋子的分布情况作为状态。
🍍确定可能的算符
- 算符是能够改变当前状态的操作或动作。需要全面考虑所有可能的有效操作,并明确它们对状态的具体影响。这些算符应该是基于问题的实际情况和规则来确定的。例如,在一个数独游戏中,算符可以是在空白格子中填入合法的数字。
- 举例:在一个路径规划问题中,算符可以是向八个方向(上、下、左、右、左上、右上、左下、右下)移动一格。
🍍建立状态空间
- 将所有可能的状态以及它们之间通过算符产生的转换关系构建成一个整体的空间或图。这需要对每个状态和算符进行系统的梳理和组织。状态空间的构建有助于直观地理解问题的复杂性和可能的解决方案路径。
- 举例:在一个迷宫问题中,状态空间可以表示为迷宫中所有可能的位置以及从一个位置到另一个位置的可行移动。
🍍考虑约束条件
- 约束条件是对状态转换和操作的限制。它们通常基于问题的物理、逻辑或资源限制等方面。例如,在资源分配问题中,可能存在资金、人力或时间的限制;在机器人运动问题中,可能存在障碍物或运动范围的限制。
- 举例:在一个背包问题中,约束条件可能是背包的容量限制和物品的重量。
🍍评估和优化状态空间表示
- 对构建好的状态空间表示进行检查和评估,看其是否清晰、准确地反映了问题,是否便于进行搜索和求解。如果发现存在问题,如状态描述过于复杂、算符定义不清晰或状态空间规模过大等,需要对其进行优化和改进。
- 举例:如果在一个优化问题中,初始的状态空间表示导致搜索效率低下,可以通过简化状态描述、减少不必要的算符或采用更有效的数据结构来优化状态空间。
🍉示例
🍈十五数码难题
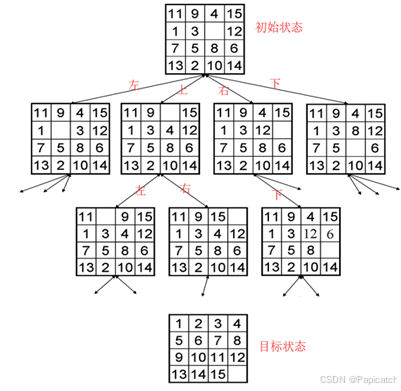
🍍问题描述
十五数码难题是在一个 4×4 的方格盘上,放有 15 个数码(1 到 15),剩下一个位置为空(用 0 表示),允许空格周围的数码移至空格,通过移动数码来将初始状态转变为目标状态。
以下是用状态空间法表示十五数码难题的具体步骤:
🍍定义问题状态
- 初始状态:S4×4 = 5,12,11,4,13,6,3,10,14,2,7,9,1,15,0,8 (其中 0 表示空格)
- 目标状态:G4×4 = 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,0
🍍确定操作符集合
- 操作符集合 F = {空格上移,空格下移,空格左移,空格右移}。这些操作可以改变空格的位置,从而产生新的状态。
🍍状态空间的解
- 是一个有限的操作算子序列,它能使初始状态转化为目标状态,即 S0 - f1 - S1 - f2 -... - fk - G。
例如,对于某个具体的十五数码初始布局,通过不断应用空格上移、下移、左移或右移这些操作,逐步改变状态,最终达到目标状态的过程,就是在状态空间中搜索解的过程。
在解决十五数码难题时,可以使用各种搜索算法,如 A*算法等,来找到从初始状态到目标状态的最优或较优的移动数码序列。
以 A*算法为例,其基本原理是在搜索的每一步都利用估价函数 f(n) = g(n) + h(n) 对 open 表中的节点进行排序,以找出最有希望的节点作为下一次扩展的节点。其中 g(n) 是在状态空间中从初始状态到状态 n 的实际代价,h(n) 是从状态 n 到目标状态的最佳路径的估计代价(启发函数)。
算法过程大致如下:
- 读入初始状态和目标状态,并计算初始状态评价函数值 f。
- 初始化 open 表和 closed 表,将初始状态放入 open 表中。
- 如果 open 表为空,则查找失败;否则:
- 在 open 表中找到评价值最小的节点,作为当前结点,并放入 closed 表中。
- 判断当前结点状态和目标状态是否一致,若一致,跳出循环;否则进行下一步。
- 对当前结点,分别按照上、下、左、右方向移动空格位置来扩展新的状态结点,并计算新扩展结点的评价值 f 并记录其父节点。
- 对于新扩展的状态结点,进行如下操作:
- 新节点既不在 open 表中,也不在 closed 表中,则添加进 open 表。
- 新节点在 open 表中,则计算评价函数的值,取最小的。
- 新节点在 closed 表中,则计算评价函数的值,取最小的。
- 把当前结点从 open 表中移除。
在实现 A*算法时,需要定义状态节点类,包含深度、启发距离、状态、哈希值、父节点等属性,还需实现生成子节点、计算距离函数(启发函数 h(n))、计算评价函数 f(n) 等函数。
计算距离函数(启发函数 h(n))可采用不同的方法,如曼哈顿距离(计算每一个位置的数据与它理论位置的横纵坐标距离之和)或欧氏距离(计算每一个位置的数据与它理论位置的直线距离之和)等。评价函数 f(n) 通常取 f(n) = g(n) + h(n),其中 g(n) 为当前结点的深度,h(n) 为启发距离。通过不断从 open 表中选择评价值最小的节点进行扩展,最终找到从初始状态到目标状态的最优路径。
🍍代码实现
import heapq import copy # 计算曼哈顿距离作为启发函数 def manhattan_distance(state, goal_state): distance = 0 for i in range(4): for j in range(4): value = state[i][j] if value!= 0: goal_row, goal_col = divmod(value - 1, 4) distance += abs(i - goal_row) + abs(j - goal_col) return distance # 检查状态是否合法(每个数字只出现一次) def is_valid_state(state): flat_state = [item for sublist in state for item in sublist] return len(set(flat_state)) == 16 # 检查状态是否为目标状态 def is_goal_state(state, goal_state): return state == goal_state # 生成可能的子状态 def generate_children(state): children = [] zero_row, zero_col = None, None for i in range(4): for j in range(4): if state[i][j] == 0: zero_row, zero_col = i, j break directions = [(0, -1), (0, 1), (-1, 0), (1, 0)] # 左、右、上、下 for dr, dc in directions: new_row, new_col = zero_row + dr, zero_col + dc if 0 <= new_row < 4 and 0 <= new_col < 4: new_state = copy.deepcopy(state) new_state[zero_row][zero_col] = new_state[new_row][new_col] new_state[new_row][new_col] = 0 if is_valid_state(new_state): children.append(new_state) return children # A* 搜索算法 def a_star_search(initial_state, goal_state): open_set = [(manhattan_distance(initial_state, goal_state), 0, initial_state)] closed_set = set() parent = {tuple(map(tuple, initial_state)): None} while open_set: _, cost, current_state = heapq.heappop(open_set) closed_set.add(tuple(map(tuple, current_state))) if is_goal_state(current_state, goal_state): path = [] while current_state is not None: path.append(current_state) current_state = parent[tuple(map(tuple, current_state))] return list(reversed(path)) children = generate_children(current_state) for child in children: child_tuple = tuple(map(tuple, child)) if child_tuple not in closed_set: new_cost = cost + 1 priority = new_cost + manhattan_distance(child, goal_state) if child_tuple not in parent or new_cost < cost: parent[child_tuple] = current_state heapq.heappush(open_set, (priority, new_cost, child)) return None # 打印状态 def print_state(state): for row in state: print(row) if __name__ == "__main__": # 初始状态 initial_state = [[5, 1, 2, 4], [9, 6, 3, 8], [13, 7, 10, 11], [0, 14, 15, 12]] # 目标状态 goal_state = [[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12], [13, 14, 15, 0]] solution = a_star_search(initial_state, goal_state) if solution: for state in solution: print("Step:") print_state(state) print("-" * 20) else: print("No solution found.")🍈猴子和香蕉问题
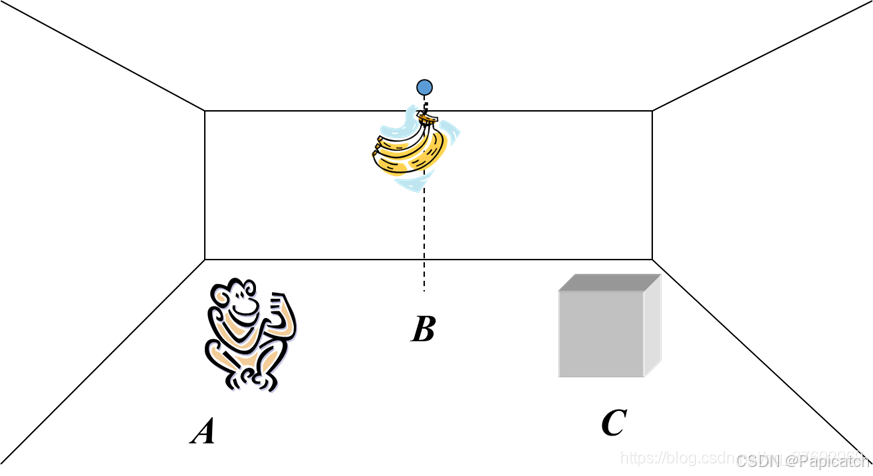
猴子和香蕉问题是人工智能中一个经典的问题表述,通常用于说明状态空间搜索和规划的概念。
以下是对猴子和香蕉问题的详细分析:
🍍问题描述
房间里有一只猴子、一个箱子和挂在天花板上够不着的香蕉。猴子可以在房间里走动、推箱子、爬上箱子够到香蕉。
🍍状态定义
- 猴子的位置(比如地面上的不同位置或在箱子上)。
- 箱子的位置。
- 猴子是否在箱子上。
例如,可以用以下方式表示状态:
- (猴子在地面 A 点,箱子在地面 B 点,猴子不在箱子上)
- (猴子在地面 C 点,箱子在地面 C 点,猴子在箱子上)
🍍操作符定义
goto(x):猴子从当前位置走到位置x。pushbox(x):猴子将箱子推到位置x(前提是猴子和箱子在同一位置)。climbbox:猴子爬上箱子(前提是猴子和箱子在同一位置且猴子在地面)。grasp:猴子在箱子上时抓取香蕉(前提是猴子在箱子上且箱子在香蕉正下方)。
🍍初始状态
(猴子在地面 A 点,箱子在地面 B 点,猴子不在箱子上)
🍍目标状态
(猴子在箱子上且箱子在香蕉正下方,猴子抓取到香蕉)
🍍状态空间
- 由所有可能的合法状态以及状态之间通过操作符的转换关系构成。状态空间的规模取决于对位置的细分程度和问题的复杂设定。
🍍解决思路
- 通过在状态空间中应用操作符,从初始状态逐步搜索到目标状态。例如,先将猴子移动到箱子所在位置,然后推动箱子到合适位置,爬上箱子抓取香蕉。
- 在实际解决过程中,可以使用不同的搜索算法,如广度优先搜索、深度优先搜索或 A* 算法等来寻找从初始状态到目标状态的路径。
- 以广度优先搜索为例,它会逐层地探索状态空间,先访问距离初始状态较近的状态,逐步扩展到更远的状态。在搜索过程中,需要维护一个已访问状态的集合,以避免重复访问和陷入死循环。
🍍代码实现
from collections import deque # 定义状态类 class State: def __init__(self, monkey_pos, box_pos, on_box, has_banana): self.monkey_pos = monkey_pos self.box_pos = box_pos self.on_box = on_box self.has_banana = has_banana def __eq__(self, other): return (self.monkey_pos == other.monkey_pos and self.box_pos == other.box_pos and self.on_box == other.on_box and self.has_banana == other.has_banana) def __hash__(self): return hash((self.monkey_pos, self.box_pos, self.on_box, self.has_banana)) def __str__(self): return f"Monkey at {self.monkey_pos}, Box at {self.box_pos}, On Box: {self.on_box}, Has Banana: {self.has_banana}" # 定义操作符 def goto(state, new_pos): if state.monkey_pos!= new_pos: new_state = State(new_pos, state.box_pos, state.on_box, state.has_banana) return new_state return None def pushbox(state, new_pos): if state.monkey_pos == state.box_pos and new_pos!= state.box_pos: new_state = State(new_pos, new_pos, state.on_box, state.has_banana) return new_state return None def climbbox(state): if state.monkey_pos == state.box_pos and not state.on_box: new_state = State(state.monkey_pos, state.box_pos, True, state.has_banana) return new_state return None def grasp(state): if state.monkey_pos == state.box_pos and state.on_box and not state.has_banana: new_state = State(state.monkey_pos, state.box_pos, state.on_box, True) return new_state return None # 广度优先搜索函数 def breadth_first_search(initial_state, goal_state): queue = deque([initial_state]) visited = set() while queue: current_state = queue.popleft() if current_state == goal_state: return True visited.add(current_state) new_states = [goto(current_state, new_pos) for new_pos in ["A", "B", "C"] if goto(current_state, new_pos)] new_states += [pushbox(current_state, new_pos) for new_pos in ["A", "B", "C"] if pushbox(current_state, new_pos)] new_states += [climbbox(current_state) if climbbox(current_state)] new_states += [grasp(current_state) if grasp(current_state)] for new_state in new_states: if new_state not in visited: queue.append(new_state) return False # 定义初始状态和目标状态 initial_state = State("A", "B", False, False) goal_state = State("C", "C", True, True) # 执行搜索 if breadth_first_search(initial_state, goal_state): print("Solution found!") else: print("No solution found.")🍉总结
状态空间法是一种强大而系统的问题解决和分析方法
它的核心在于通过对问题状态的精确描述、操作符的定义以及状态空间的构建,来全面理解和解决问题。
首先,状态的清晰定义能够准确捕捉问题在不同时刻的具体情况,为后续的分析提供基础。
操作符则规定了状态之间的转换方式,使我们能够从一个状态过渡到另一个状态。
通过构建状态空间,将所有可能的状态以及它们之间的转换关系以直观的方式呈现出来,有助于我们从整体上把握问题的复杂性和潜在的解决方案。
状态空间法具有广泛的应用,适用于各种领域的问题,如人工智能中的搜索和规划、工程系统的建模与控制、游戏策略的制定等。
它不仅能够帮助我们找到问题的解,还能在解的过程中揭示问题的结构和特点。
然而,状态空间法也面临一些挑战。对于复杂问题,状态空间可能会变得非常庞大,导致计算和搜索的难度增加。因此,在实际应用中,常常需要结合启发式信息、剪枝策略和优化算法来提高求解效率。
总的来说,状态空间法为解决复杂问题提供了一种有条理、全面且可操作的框架,是许多领域中不可或缺的工具。