Hi,大家好,我是半亩花海。接着上次的多重回归继续更新《白话机器学习的数学》这本书的学习笔记,在此分享随机梯度下降法这一回归算法原理。本章的回归算法原理还是基于《基于广告费预测点击量》项目,欢迎大家交流学习!
目录
一、随机梯度下降法概述
随机梯度下降法是一种优化算法,用于最小化目标函数,即减少模型预测和实际结果之间的差距。它是梯度下降算法的一种变体,其核心原理是在每次迭代搜索中,算法随机选择一个样本或数据点(或一小批样本),计算该样本的梯度,然后用这个梯度更新模型参数。
随机梯度下降算法(Stochastic Gradient Descent,SGD)和批量梯度下降算法(Batch Gradient Descent,BGD)的区别在于:随机梯度算法每次只使用少数几个样本点或数据集(每次不重复)的梯度的平均值就更新一次模型;而批量梯度下降算法需要使用所有样本点或数据集的梯度的平均值更新模型。、
举一个经典而形象的例子:假设你现在在山上,为了以最快的速度下山,且视线良好,你可以看清自己的位置以及所处位置的坡度,那么沿着坡向下走,最终你会走到山底。但是如果你被蒙上双眼,那么你则只能凭借脚踩石头的感觉判断当前位置的坡度,精确性就大大下降,有时候你认为的坡,实际上可能并不是坡,走一段时间后发现没有下山,或者曲曲折折走了好多路才能下山。类似的,批量梯度下降法就好比正常下山,而随机梯度下降法就好比蒙着眼睛下山。
因此,随机梯度下降算法的效率明显提高,目前已经得到了广泛应用。
例子来源于:《详解随机梯度下降法(Stochastic Gradient Descent,SGD)_随机梯度下降公式-CSDN博客》
二、案例分析
1. 设置问题
在介绍随机梯度下降法之前,我们先得知道之前研究过最速下降法,它除了计算花时间以外,还有一个缺点那就是容易陷入局部最优解。
在讲解回归时,我们使用的是平方误差目标函数。这个函数形式简单,所以用最速下降法也没有问题。现在我们来考虑稍微复杂一点的,比如这种形状的函数:
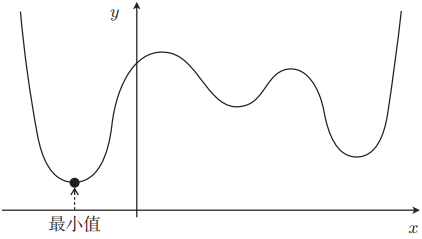
用最速下降法来找函数的最小值时,必须先要决定从哪个  开始找起。之前我用
开始找起。之前我用  说明的时候是从
说明的时候是从  或者
或者  开始的,那是为了讲解而随便选的作为初始值。选用随机数作为初始值的情况比较多。不过这样每次初始值都会变,进而导致陷入局部最优解的问题。
开始的,那是为了讲解而随便选的作为初始值。选用随机数作为初始值的情况比较多。不过这样每次初始值都会变,进而导致陷入局部最优解的问题。
假设这张图中标记的位置就是初始值:
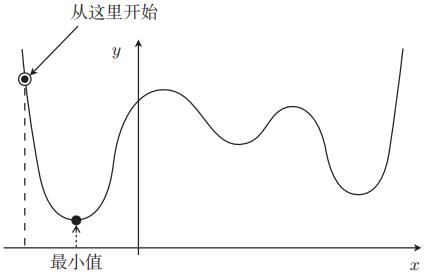
倘若从这个点开始找,似乎可以求出最小值。但是如果我们换一个初始点,如下所示,那么可能没计算完就会停止,便陷入了局部最优解。
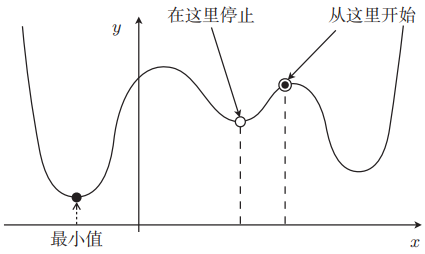
这个算法虽然简单,但是容易发生各种问题,但最速下降法也不会白学,随机梯度下降法就是以最速下降法为基础的。
2. 定义模型
由 《机器学习 | 回归算法原理——最速下降法(梯度下降法)-CSDN博客》可知,最速下降法的参数更新表达式为:

这个表达式使用了所有训练数据的误差,而在随机梯度下降法中会随机选择一个训练数据,并使用它来更新参数。下面这个表达式中的  就是被随机选中的数据索引。
就是被随机选中的数据索引。

最速下降法更新 1 次参数的时间,随机梯度下降法可以更新  次。 此外,随机梯度下降法由于训练数据是随机选择的,更新参数时使用的又是选择数据时的梯度,所以不容易陷入目标函数的局部 最优解,在实际运用上的确会收敛。
次。 此外,随机梯度下降法由于训练数据是随机选择的,更新参数时使用的又是选择数据时的梯度,所以不容易陷入目标函数的局部 最优解,在实际运用上的确会收敛。
3. 随机梯度下降法(拓展)
我们前面提到了随机选择 1 个训练数据的做法,此外还有随机选择  个训练数据来更新参数的做法。设随机选择
个训练数据来更新参数的做法。设随机选择  个训练数据的索引的集合为
个训练数据的索引的集合为  ,则更新参数如下:
,则更新参数如下:

现在假设训练数据有 100 个,那么在  时,创建一个有 10 个随机数的索引的集合,例如
时,创建一个有 10 个随机数的索引的集合,例如  ,然后重复更新参数,这种做法被称为小批量(mini-batch)梯度下降法。 这像是介于最速下降法和随机梯度下降法之间的方法。
,然后重复更新参数,这种做法被称为小批量(mini-batch)梯度下降法。 这像是介于最速下降法和随机梯度下降法之间的方法。
ps:不论是随机梯度下降法还是小批量梯度下降法,我们都必须考虑学习率 ,将
,将  设置为合适的值是尤为重要。
设置为合适的值是尤为重要。
