定义明晰
中短期预测(短期:1年内;中期:2-5年):例如天气预报、股票价格预测、销售量预测等。
长期预测(5-10年及以上):例如人口增长、能源消耗、气候变化等。
一、拟合、插值预测
中短期预测 数据需求小2/10/100
自变量(多个)+因变量(一个) 不可反推
1.插值与拟合之间的区别?
插值:原则上曲线要通过图像中给出的点
拟合:原则上不需要经过图像中的任何一个点,只要保证与各点的距离总体足够小即可
2.插值的主要方法?
①分段线性插值:把已知相邻的两个点连起来,预测中间的值,但是用来预测未来的值误差极大
②三次样条插值:如有韧性的木条,光滑曲线,可以显著降低月误差,但是总体不如高阶的拟合
3.拟合的主要方法?
①最小二乘法:图像上与散点的y值相差平方和最小的一个解法,最为方便,也比较可信
②卡尔曼滤波、进阶最小二乘、高次函数拟合…
【附】matlab插值实现:
插值点:在一个已知的数据点集合中,我们希望通过某种方法来估计或推断出其他位置的数值。
被插值点:我们希望获得插值结果的位置。
【附1】一维插值
yi = interp1(x,y,xi,'method')
%x,y为插值点,xi,yi为被插值点和结果,x,y和xi,yi通常为向量
%'method'表示插值方法:常用的有'nearest''linear''spline''cubic'
%spline:三次样条插值,构造三次多项式进行差值
【代码示范】
x=[1,2,3,4,5];
y=[1,2,3,4,5];
xi=1:0.5:5;
yi = interp1(x,y,xi,'spline');
【附2】二维插值
zi = interp2(x,y,z,xi,yi,'method')
%x,y,z为插值点,xi,yi为被插值点,zi为输出的插值结果,即插值函数在(xi,yi)处的值;x,y为向量,xi,yi为向量或矩阵,z和zi为矩阵
%'method'表示插值方法:常用的有'nearest''linear''spline''cubic'
'nearest'表示最近邻插值,即用最近的已知点的值来估计未知点的值。
'linear'表示线性插值,即用两个最近的已知点之间的线性函数来估计未知点的值。
'spline'表示样条插值,即用一组光滑的多项式函数来逼近已知点,并在这些函数之间进行插值。
'cubic'表示三次样条插值,是样条插值的一种特殊情况,其中每个多项式函数都是三次的。
【代码示范】
x = 1:5;
y = 1:3;
temps = [82 80 81 82 84;79 63 61 65 81;84 84 82 85 86];
xi = 1:.2:5;
yi = 1:.2:3;
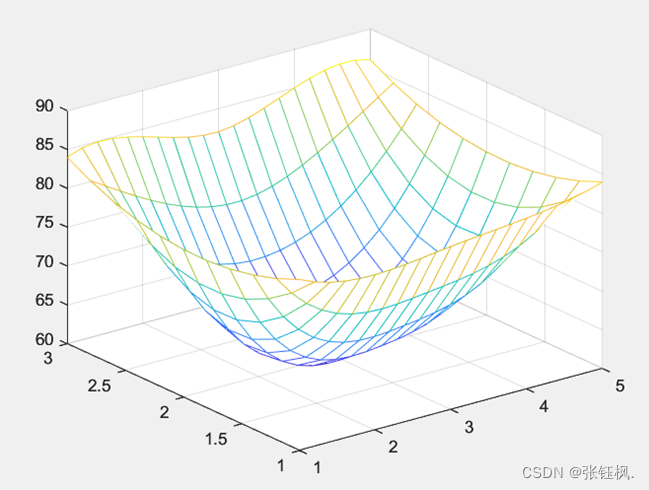
zi = interp2(x,y,temps,xi',yi,'spline');
mesh(xi,yi,zi)
二、线性回归
中短期预测 数据需求中10/100/1000
自变量(多个)+因变量(一个) 可反推
- 简单线性回归:一个自变量和一个因变量(线性,一&一)
- 多元线性回归:多个自变量和一个因变量(线性,多&一)
- 岭回归(L2正则化):系数缩小,减小过拟合(解决过拟合,系数缩小)
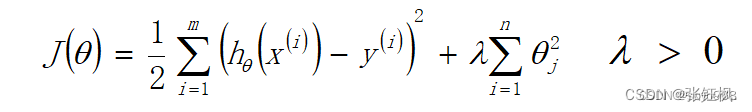
- lasso(L1正则化):一些系数变为0,特征选择(解决过拟合,系数为0)
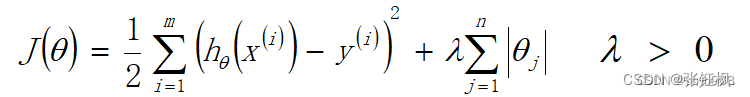
- 局部加权线性回归:非参数回归方法(非线性)
【补充】 “非参数”指的是该方法不需要对模型的形式、参数等进行假设,而是通过对每个测试点周围的训练点进行加权来进行预测。
线性回归每一个样本对应相同的回归系数👉易欠拟合
局部加权线性回归每一个样本都有一个自己的回归系数👉拟合度好但计算量大
适用场景:数据集小、其他模型欠拟合
- 多项式回归:数据升维+线性回归(非线性)
数据升维后增加了特征,有利于解决欠拟合问题
局部加权线性回归与多项式回归之间的区别?
多项式回归适用于解决欠拟合问题。
局部加权线性回归则更适用于解决过拟合问题。
同时,还可以考虑使用正则化方法(如岭回归和Lasso回归)
三、时间序列模型
中短期预测 数据需求小12/36/60
因变量(一个)(时间序列数据) 不可反推
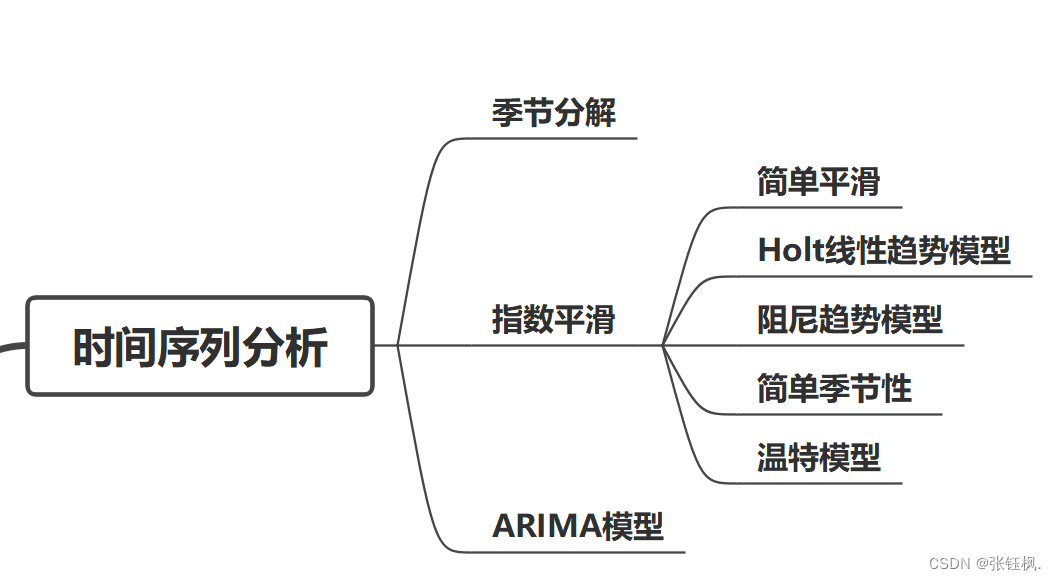
- 具有明显的季节性:季节分解
- 没有季节性但具有平稳趋势:指数平滑
- 没趋势&没季节性:简单平滑
- 有趋势&没季节性:线性关系:Holt线性趋势模型
非线性关系:阻尼趋势模型(非线性关系)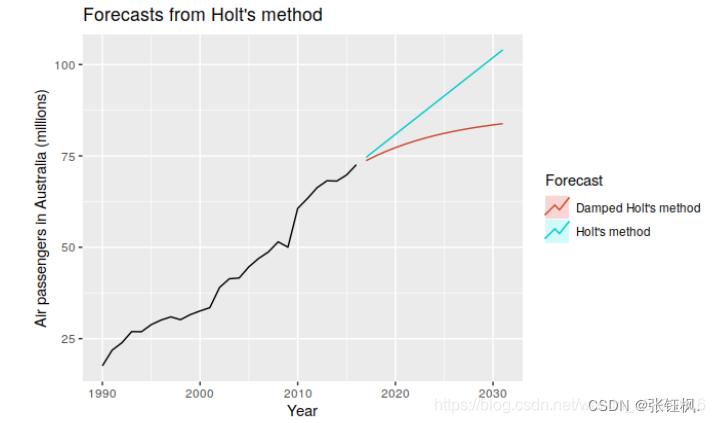
- 没趋势&有季节性:简单季节性
- 有趋势&有季节性:温特趋势
- 具有复杂趋势和季节性:ARIMA模型
四、Logistic回归(逻辑回归)
长期预测 数据需求中10/100/1000
自变量(多个)+因变量(一个) 不可反推
要求:①变量之间的相关性需要比较小 ②样本的个数需要大于三倍自变量个数
缺点:容易欠拟合,一般准确度不太高
应用: 最经典的是:葡萄酒规划的问题上(好多因变量共同评价葡萄酒的品质)
补充:①逻辑回归结果很差情况下,决策树一般会比较好解决,适合少量样本多维特征情况
②可以考虑降维方法之后再用逻辑回归
③在有很多因变量的时候,可以用主成分分析或者聚类分析来减少自变量
五、神经网络预测
长期预测 数据需求大50/500/5000
自变量(多个)+因变量(一个) 可反推
重点在于大量数据和异常值&缺失值的处理(重点!避免简单删除替换)
1.交代清楚输入输出&迭代次数、学习率等超参数
2.神经网络层数和结点数
3.评价标准很重要(准确率,损失函数,稳定性…)
六、微分方程预测
中短期预测 数据需求小2/10/100
因变量(一个)(微分方程的解) 不可反推
找不到数据之间的关系,但是能找到变化量之间的关系的时候用
七、灰色预测
中短期预测 数据需求小4/10/50
因变量(一个) 不可反推
理论性不强,没法论证,能不用就不用,数据量非常少的时候可以考虑
八、马尔科夫链预测
中短期预测 数据需求中10/100/1000
因变量(一个)(状态转移) 不可反推
序列之间前后传递比较少的,数据和数据之间随机性比较强(比如今明天的气温没有直接联系,只能从趋势判断后天温度是多少)
