零点与极点

目录：

1、传递函数

2、波特图零点与极点

零极点又称初始极点或者主极点，是分析电路中的物理学名词，主要的作用是用来分析电路的频率特性、系统的稳定性。此外，还可以得出系统的时域响应等相关方面的参数。

1、传递函数

电路中传递函数可以理解为放大倍数。图2.48所示的电路由运放隔离成前后两级，第一级为高通滤波(截止频率fL ≈ 1.6Hz)，第二级为低通滤波(截止频率fH ≈ 16.2kHz)。

1）按照前后级截止频率，可以粗略理解为大于 1.6Hz 和小于 16.2kHz 的信号可以通过滤波器。所以图1所示电路为带通滤波器。

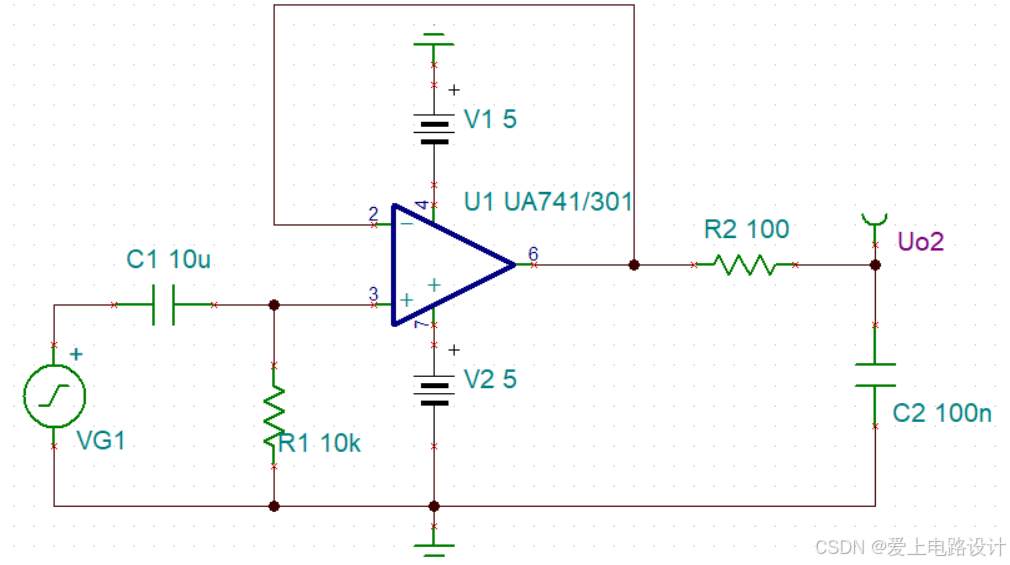
图1 带通滤波器电路

2）假定前一级放大倍数为 A1，第二级放大倍数为 A2，总的放大倍数为 A = A1*A2。按阻抗分压原理，可以很容易得到式1。

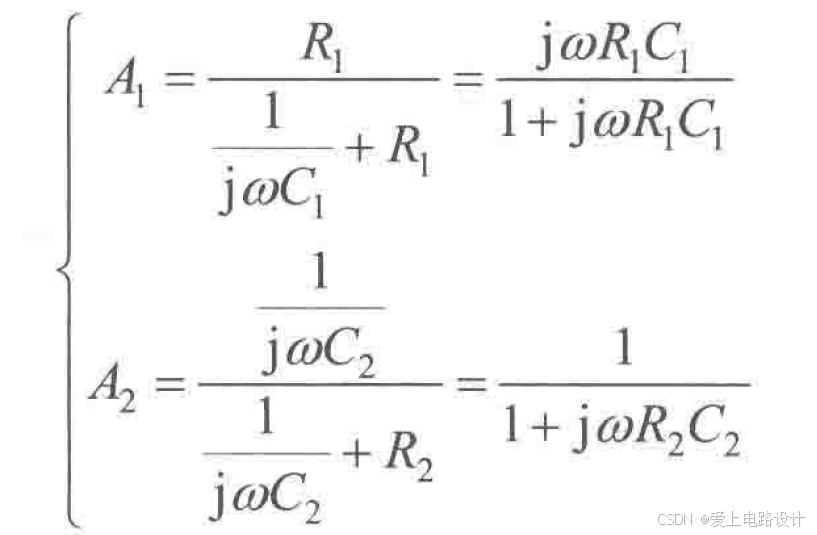
式1  通过阻抗分压

3）用 s 替代式1中的 jω (拉普拉斯变换)，就可以得到式2，使分子为零的 s 称为零点，使分母为零的 s 称为极点。分母中 s 的最高指数称为滤波器的阶数。

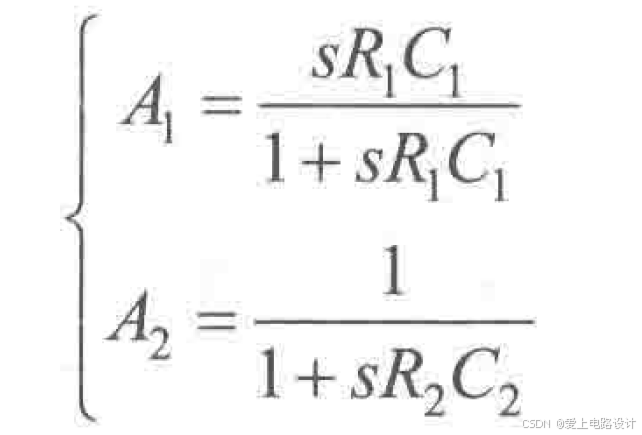
式2  拉氏变换

4）通过式2可以看出，A1 代表的高通滤波器有一个零点(0Hz)和一个极点(16.2kHz)，A2 代表的低通滤波器只有一个极点(1.6Hz)。A1 和 A2 合成的带通滤波器的阶数为 2 阶。

2、波特图零点与极点

通过式2可得，在图1所示的带通滤波器中，存在 0Hz 零点、1.6Hz 和 16.2kHz两个极点。关于零、极点在波特图的物理意义总结如下。

1）零点处幅频特性曲线的斜率变化 20dB/10倍频(频率每增加10倍，幅值下降dB)，相移 45°。

2）极点处幅频特性曲线的斜率变化 -20dB/10倍频，相移-45°。

图2所示为带通滤波器的幅频和相频特性曲线。

图2 带通滤波器的幅频和相频特性曲线

1）0Hz零点处(TINA仿真无法从0Hz开始)，幅频特性曲线开始有 20dB/10倍频的斜率。

2）零点处的相移是 45°，但在远小于零点处，相移为90°，所以相频特性曲线从 90° 开始。

3）在第一个极点 1.6Hz 处，幅频特性曲线变化 -20dB/10倍频，所以 1.6Hz 以后幅频特性曲线变为水平。

4）1.6Hz 极点处会发生 -45° 相移，所以 1.6Hz 处总相移为90°-45° = 45°。在远离 1.6Hz 极点处比如 1.6Hz 以后，总相移变为 90°-90° = 0°。

5）在第二个极点 16.2kHz 处，幅频特性曲线变化 -20dB/10倍频，所以 16.2kHz 以后幅频特性曲线变为 -20dB/10倍频。

6）16.2kHz 极点处会发生 -45° 相移，所以 16.2kHz 处总相移为90°-90°-45° = 45°。在远离16.2kHz 极点处，比如 16.2kHz 以后，总相移变为 90°-90°-90° = 90°。

本节内容采用TINA-TI软件仿真(TINA-TI的介绍与入门使用)，仿真原文件下载移步：零点与极点。

把问题时时放在心头，直到一点曙光逐渐破晓终而变成阳光普照。觉得不错，动动发财的小手点个赞哦！