问题分析
设计并发程序的目的就是为了使程序运行得更快(时间就是金钱、生命),提高软件的性能。并发程序之所以能快,就在于这个“并”字,因为程序能并发(单核)或并行(多核、多CPU)执行,当然能快。这就好比工人搬砖块,人当然是越多越快。但是,这之中有个关键问题,大家是否想到,那就是这个事情(如搬砖块)是否可以并发或并行来做。
例如每个人乘车去上班这件事就没法并发来做,因为从起点到终点,公交车只能是一站一站到达,同一辆车不可能同时达到几个站,也不可能给你增加几台公交车(多核,多线程),你的乘车时间因此减少了,所以这个时候,给你再多的车(增加CPU或核心数),你的乘车时间也不会减少(程序性能提高不了),因此这个时候,你只能希望汽车跑得更快(提高单个CPU或核心的运算速度),这样才能达到减少时间提高程序性能的目的。这就说明了,并发程序设计的一个本质问题,就是首先要分析问题能不能让程序去并发或并行执行?如果这个问题(乘公交车上班)本身就只能串行去做,那么您就不用考虑使用并发编程技术了,因为这不但不能提高效率反而会使程序开发变得更加复杂,得不偿失。
在确定需要使用并发编程技术来解决问题后,我们应该进一步分解问题,其实现实世界中广泛存在两类可以并发处理的问题场景:一种是可以完全并发或并行(如访问网站,银行窗口办业务等),这当然是绝佳的并发编程应用场景;还有一种则是总体需要串行,但中间有些步骤可以并发执行(事实上所有能并发处理的问题都是这种类型,只是看具体问题规模及分解情况),这个时候就需要处理依赖(前置步骤)与等待(同步)问题,最终按顺序完成。所以我们需要把问题进行逐步分解,以便最大化利用并发编程的优势。
引入并发程序解决问题时,目的是为了加快程序运行速度,减少时间。但是你肯定想知道快了多少,是否达到你的预期。这个数据不难得出,只要在同等条件下,把并发之前与之后的程序运行时间对照一下就能看出来。通常人们把程序优化之前运行时间与优化之后的时间的比值称之程序加速比。它是用来衡量程序优化效果的一个关键参数。
程序加速比 = 优化前耗时 / 优化后耗时
由此,我们引入计算机科学中非常重要的定律——Amdahl定律。它定义了串行系统并行化后加速比的计算公式与理论上限,并给出了加速比与系统并行程度和处理器(CPU)数量的关系。设加速比为Speedup,系统内必须串行化的部分比重为F ,CPU数量为N ,则有公式:
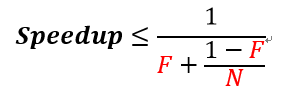
当处理器(CPU)的数量N 趋于无穷大时,Speedup 的最大值无限趋近1/F ,那么加速比与系统的串行化率成反比。这意味着如果程序中有50%(F)的处理都需要串行进行的话,Speedup 只能提升2倍;如果程序中有10%(F)需要串行进行,Speedup 最多能够提高近10倍。
Amdahl定律同时量化了串行化的效率开销。在拥有10个处理器的系统中,程序如果有10%是串行化的,那么最多可以加速5.3倍(53%的使用率),在拥有100个处理器的系统中,这个数字可以达到9.2(92%的使用率)。即使有无限多个CPU(N),程序加速比也不可能为10。
根据Amdahl定律,使用并发编程技术解决问题时,系统运行速度的快慢主要取决于CPU或核心的数量及系统中串行化程序的比重。CPU或核心数量越多,串行化比重越低,则系统运行速度越快。仅提高CPU或核心数量而不降低系统串行化程序的比重,也是无法加快系统的运行速度,提高系统的性能。
线程数和任务数

共享可变性
你可能会想“只要把任务进行分解并分派到多个线程中执行,程序就能获得更高的吞吐量”。但遗憾的是,绝大多数问题都无法被分解为彼此完全独立的几个子问题。更普遍的情况是,我们可以独立地执行某些操作,但最终还是需要将这些操作所得到的部分结果进行归并才能得到完整的结果。所以线程之间需要能够相互交换彼此的数据,并且有时候某些线程还需要等待其他线程的结果出来之后才能继续运行。于是我们就需要在线程之间进行协调,并由此引出同步和锁等一系列令人头痛的问题。在开发并发应用程序的时候,我们通常会遇到3类问题:饥饿、死锁以及竞争条件,这三类问题都与线程同步及锁有很大的关系,其中前两个问题还算比较易于检测甚至避免,而竞争条件则是一个需要彻底根除的棘手问题(因为它是很容易让并发程序产生bug,而且很多时候很难跟踪与调试)。
共享可变性方法,也是我们常用的方法,我们创建的变量允许所有线程修改,当然是在一个可控的模式下。使用共享可变性来进行编程虽然看似简单,但却可能会导致同步问题。为了使用共享可变性,我们必须保证不会有两个线程同时修改同一个字段,并且对多个字段的修改必须满足一致性原则,因为这样写出来的程序在同步方面太容易出错了。
